Додатки

1. Вектор.

Геометричний вектор — це направлений відрізок в просторі. Довжина вектора називається його модулем і позначається: .

У прямокутній декартовій системі координат кожен вектор можна однозначно представити у вигляді , де — одиничні вектори (орти) по осях координат x, y, z. Числа називаються прямокутними декартовими координатами вектора .

Модуль вектора можна визначити за його декартовими координатами

2. Скалярний добуток векторів.

С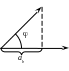 калярний добуток векторів і є число

,

де - кут між векторами і .

3. Векторний добуток векторів.

П ід векторним добутком векторів і розуміють вектор що має довжину (площа паралелограма, побудованого на і , як на сторонах) і направлений перпендикулярно до і , причому так, що вектори і і утворюють праву трійку векторів.

Позначення:

4. Поняття похідної функції.

Функція f називається диференційованою в точці x₀, якщо існує границя відношення різниці функції f у точці x₀

Ця границя називається похідною функції f у точці x₀ і позначається:

, , ,

5. Похідні деяких елементарних функцій.

6. Частинна похідна.

Нехай функція f визначена в деякій околиці точці . Функція f називається диференційованою по , якщо існує границя різницевого відношення

.

Ця границя називається частинною похідною функції в точці Р₀ і позначається

або .

7. Повний диференціал функції f в точці Р₀:

8. Визначений інтеграл.

Нехай функція f(x) визначена і обмежена на відрізку [а,b]. Розіб'ємо цей відрізок на "елементарні" відрізки введенням n точок x_i таким чином:

Позначимо через dx довжину елементарного відрізка . У кожному елементарному відрізку виберемо довільне число . Число називається інтегральною сумою.

Функція називається інтегрованою на відрізку [а,b], якщо існує число I з наступною властивістю: для будь-якого знайдеться таке , що при будь-якому розбитті на відрізки dx, для якого , виконується нерівність незалежно від вибору .

Число I називається визначеним інтегралом функції f(x) на відрізку [а,b] і позначається: . Тут х називається змінною інтегрування, а і b — відповідно нижньою і верхньою границями інтегрування.

9. Градієнт.

Градієнтом поля U( ) називається вектор, який визначається в кожній точці поля співвідношенням:

.

Часто вектор позначають також , де ("набла") позначає символічний вектор, який називається оператором Гамільтона або набла-оператором: .

В будь-якій точці поля величини U( ) градієнт поля спрямований у напрямку зростання цієї величини із цієї точки.

ГРЕЦЬКА АБЕТКА

Прописні	Рядкові	Назва	Прописні	Рядкові	Назва	Прописні	Рядкові	Назва
Α	α	Альфа	Ι	ι	Йота	Ρ	ρ	Ро
Β	β	Бета	Κ	κ	Каппа	Σ	ς, σ	Сігма
Γ	γ	Гамма	Λ	λ	Лямбда	Τ	τ	Тау
Δ	δ	Дельта	Μ	μ	Мю	Υ	υ	И-псілон
Ε	ε	Е-псілон	Ν	ν	Ню	Φ	φ	Фі
Ζ	ζ	Дзета	Ξ	ξ	Ксі	Χ	χ	Хі
Η	η	Ета	Ο	ο	О-мікрон	Ψ	ψ	Псі
Θ	θ	Тета	Π	π	Пі	Ω	ω	О-мега

ПРИСТАВКИ ДО ПОЗНАЧЕНЬ ОДИНИЦЬ

фемто	10-15	ф	f	мілі	10-3	м	m	гекто	102	г	h
піко	10-12	п	р	санті	10-2	c	c	кіло	103	к	к
нано	10-9	н	n	деці	10-1	д	d	мега	106	М	М
мікро	10-6	мк	μ	дека	10	да	da	гіга	109	Г	G