2.3 Другий закон термодинаміки. Рідини. Ентропія.

Кількість теплоти δQ, яка повинна бути передана до системи або відведена від неї при переході від одного стану до іншого, не визначається однозначно початковим і кінцевим станами, а суттєво залежить від способу здійснення цього переходу (δQ не є функцією стану системи). Однак, приведена кількість теплоти – відношення теплоти δQ до температури Т системи при нескінченно малих змінах стану системи – є функцією стану системи. В будь-якому оборотному круговому процесі

.

Відповідно, підінтегральний вираз є повний диференціал деякої функції, яка визначається тільки початковим і кінцевим станами системи і не залежить від шляху, яким система прийшла в цей стан.

Ентропією S називається функція стану системи, диференціалом якої є :

.

Тобто перший закон термодинаміки можна записати у вигляді

,

звідки .

Функція є функцією стану системи і називається енергією Гельмгольца або вільною енергією.

В замкненій системі для оборотних процесів ΔS = 0; для необоротних циклів ΔS > 0.

Нерівність Клаузиуса: ентропія замкненої системи може або збільшуватися (у випадку необоротних процесів), або залишатися незмінною (у випадку оборотних процесів).

Оскільки і мають один і той же знак, то по характеру зміни ентропії можна зробити висновок про напрямок процесу теплообміну. При нагріванні тіла і його ентропія збільшується , при охолодженні і ентропія тіла зменшується . Ізоентропійним називається процес, який протікає при постійній ентропії (S = const). В оборотному адіабатичному процесі , так що і S = const, тому адіабатичний процес є ізоентропійним.

Розглянемо для приклада ідеальний газ, який здійснює рівноважний перехід із стану 1 в стан 2. Зміна його ентропії

Використовуючи ; ;

.

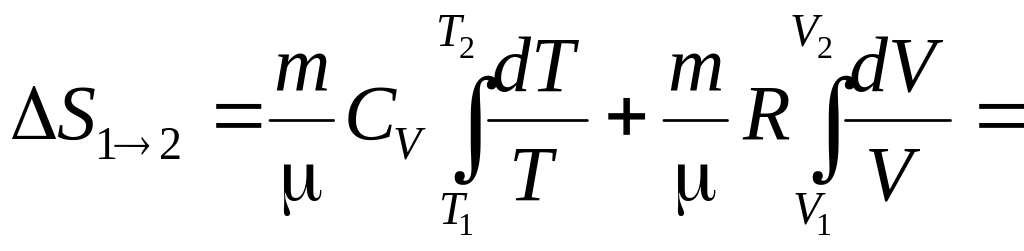
Зміна ентропії в процесах ідеального газу

Ізохорний (V = const)	Ізобаричний (р = const)	Ізотермічний (Т = const)	Адіабатичний (S = const)

Статистичне тлумачення ентропії.

Термодинамічна ймовірність W стану тіла чи системи – це число способів, якими може бути реалізований даний конкретний термодинамічний стан (макростан). Або інакше кажучи, це число всіх можливих мікророзподілів частинок за координатами та швидкостями (мікростанів), які відповідають даному термодинамічному стану.

Формула Больцмана: , де k – стала Больцмана.

Ентропія системи є логарифмом числа мікростанів, за допомогою яких може бути реалізовано даний макростан. Ентропія є мірою невпорядкованості системи – чим більше число мікростанів, які реалізують даний макростан, тим більше ентропія.

Всі процеси в замкненій системі ведуть до збільшення її ентропії. В замкненій системі процесі протікають в напрямку від менш ймовірних станів до більш ймовірних, до того часу, доки ймовірність стану не стане максимальною. В стані рівноваги – найбільш ймовірного стану системи – число мікростанів максимально, при цьому максимальна й ентропія.

Другий закон термодинаміки.

Будь – який необоротний процес в замкненій системі відбувається так, що ентропія системи при цьому збільшується (закон збільшення ентропії).

Перший закон термодинаміки є законом збереження та перетворення енергії стосовно термодинамічних процесів. Другий закон термодинаміки визначає напрямок протікання термодинамічних процесів, вказуючи, які процеси в природі можливі, а які – ні.

Існують ще два визначення другого закону термодинаміки, еквівалентних закону збільшення ентропії:

– по Кельвіну: неможливий круговий процес, єдиним результатом якого є перетворення теплоти, одержаної від нагрівача, в еквівалентну їй роботу;

– по Клаузіусу: неможливий круговий процес, єдиним результатом якого є передача теплоти від менш нагрітого тіла до більш нагрітому.