Лінійна швидкість.

Швидкість — це векторна величина, яка визначає як швидкість руху, так і його напрям в даний момент часу.

Вектором середньої швидкості за інтервал часу t називається відношення приросту радіусу-вектора точки до проміжку часу t

.

Напрям вектора середньої швидкості співпадає з напрямом .

Одиниця швидкості — м/с.

Миттєва лінійна швидкість — векторна величина, що дорівнює першій похідній (Додаток 4) по часу від радіусу-вектора даної точки

.

В декартовій системі складові вектора визначаються як похідні відповідних координат точки:

; ; .

Вектор миттєвої швидкості завжди спрямований по дотичній до траєкторії у сторону руху. Модуль миттєвої швидкості (скалярна величина) дорівнює першій похідній шляху по часу

.

При нерівномірному русі модуль миттєвої швидкості з часом змінюється. Тому можна ввести скалярну величину — середню швидкість нерівномірного руху (інша назва — середня швидкість шляху)

.

Переміщення точки , зміну її координат x, y, z і пройдений шлях s за проміжок часу t (від t₁ до t₂) знаходяться як інтеграли (Додаток 8):

; ; ; ; .

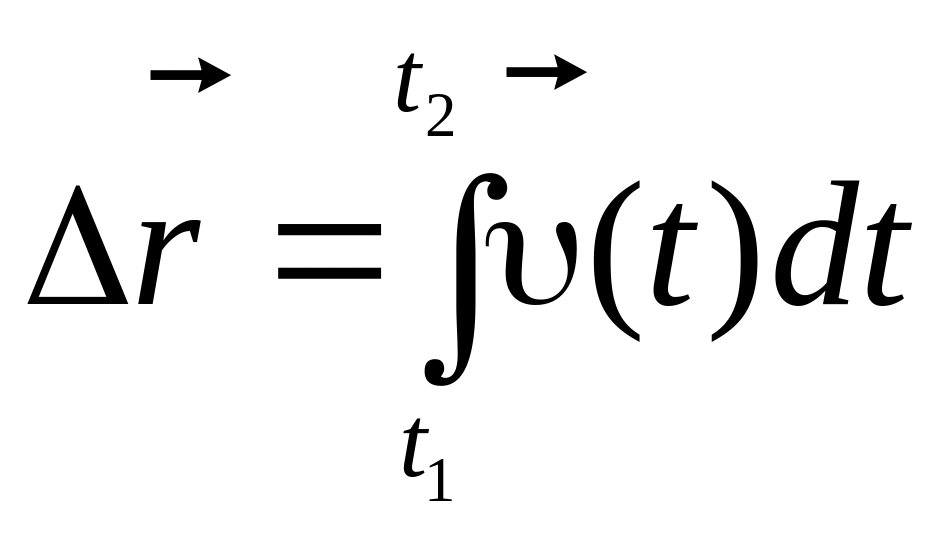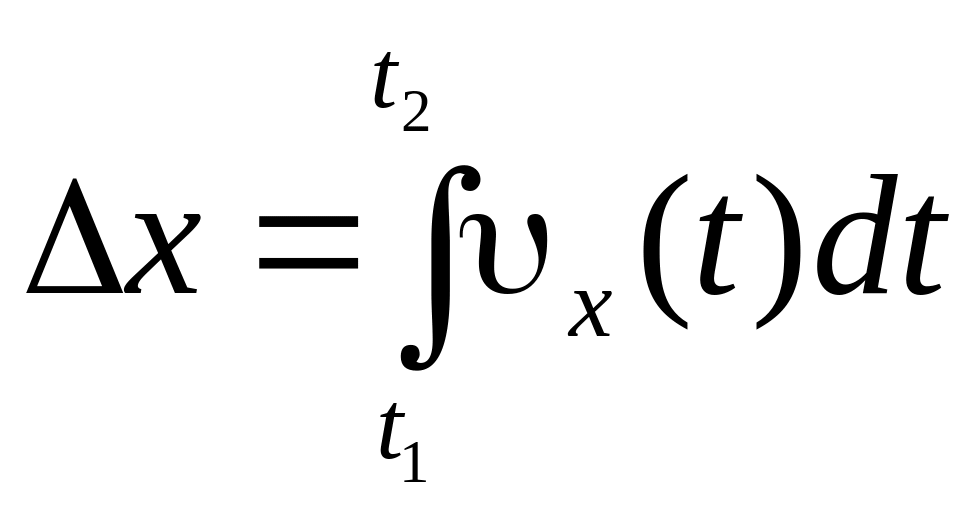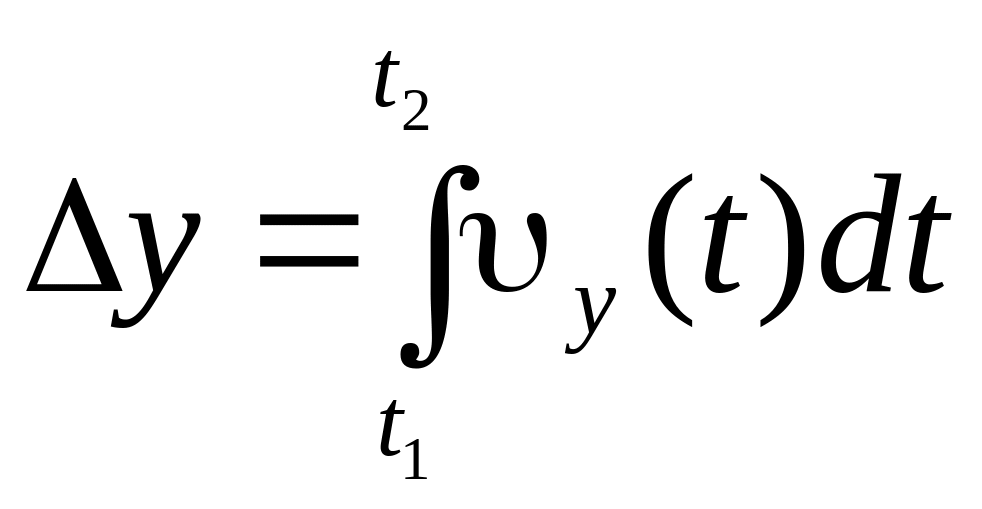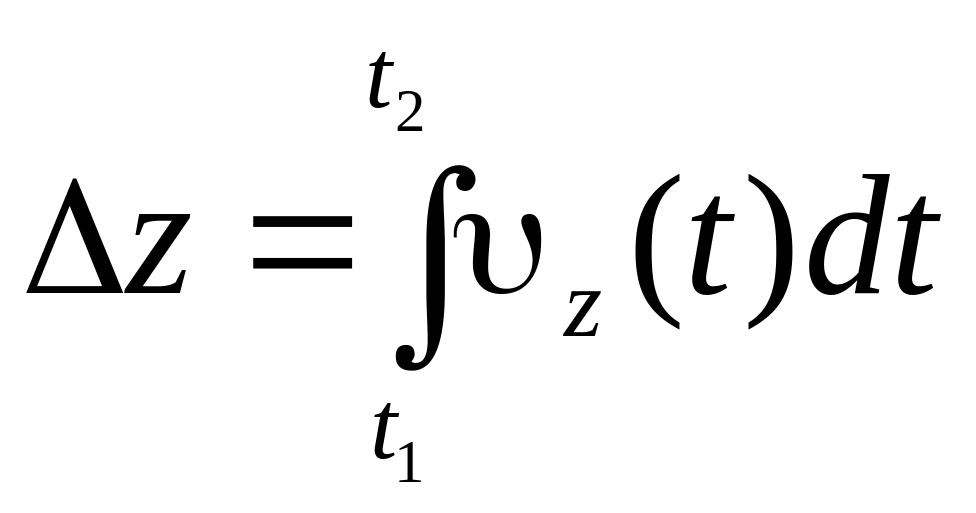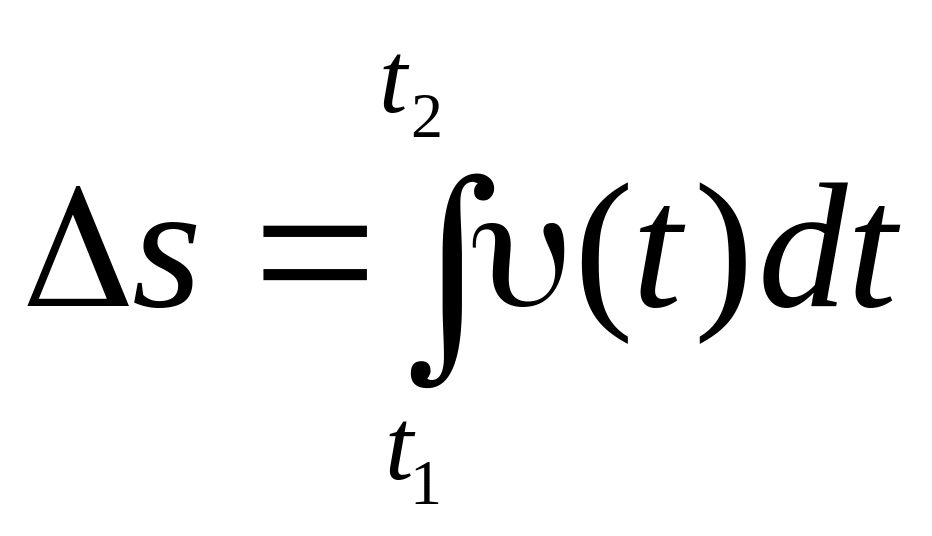При прямолінійному русі точки напрям вектора швидкості зберігається незмінним.

Рух точки називається рівномірним, якщо модуль її швидкості не змінюється з часом , для нього

.

Якщо модуль швидкості збільшується з часом, то рух називається прискореним, якщо ж він убуває з часом, то рух називається сповільненим.

Лінійне прискорення.

Прискорення — це векторна величина, що характеризує зміну швидкості з часом по модулю і напряму.

Середнє прискорення в інтервалі часу t — векторна величина, що дорівнює відношенню зміни швидкості до інтервалу часу t

.

Миттєве лінійне прискорення матеріальної точки — векторна величина, що дорівнює першій похідній швидкості даної точки (другої похідної від радіусу-вектора цієї ж точки) по часу:

Одиниця прискорення — м/с².

В декартовій системі складові вектора прискорення визначаються як похідні відповідних складових швидкості або другі похідні координат точки:

; ; .

У загальному випадку криволінійного руху вектор прискорення зручно представити у вигляді суми двох проекцій

Т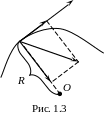 ангенціальне прискорення характеризує зміну модуля швидкості з часом. Цей вектор спрямований по дотичній к траєкторії (рис. 1.3) в напрямку швидкості при прискореному і протилежно при сповільненому русі, а його величина

.

Нормальне (доцентрове) прискорення направлене по нормалі від траєкторії до центру її кривизни О (рис. 1.3) і характеризує зміну напряму вектора швидкості точки. Величина нормального прискорення a_n зв'язана з модулем швидкості і величиною радіусу кривизни траєкторії R

Величина повного прискорення

Зміну вектора швидкості точки , зміни його складових , , і модуля за проміжок часу t (від t₁ до t₂) знаходяться як інтеграли:

; ; ; ; .

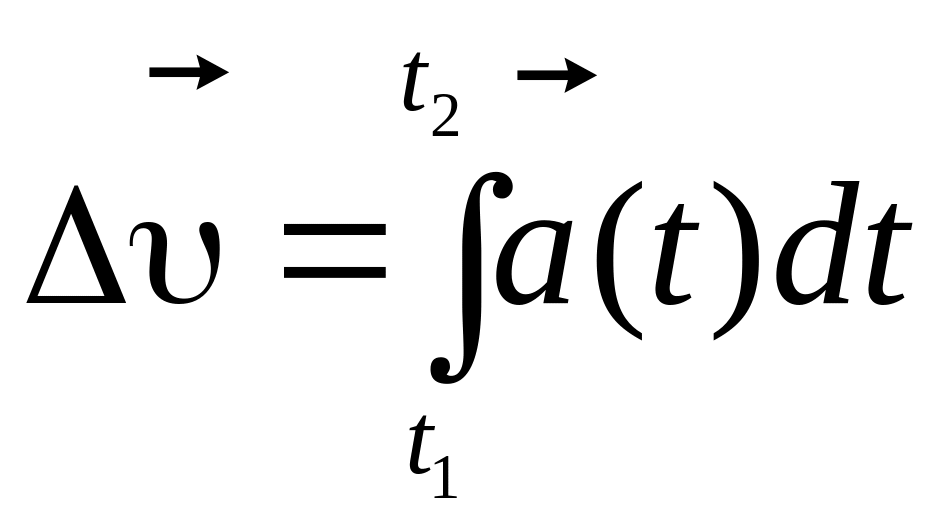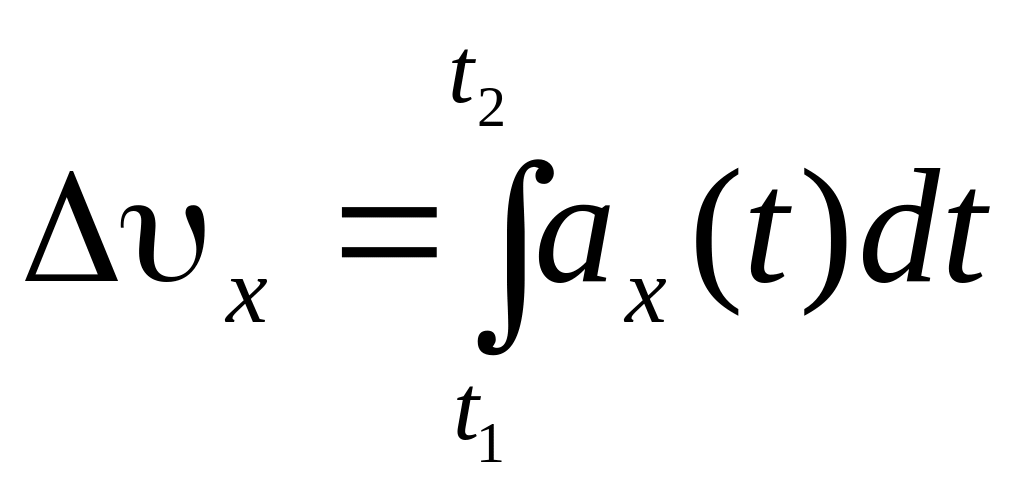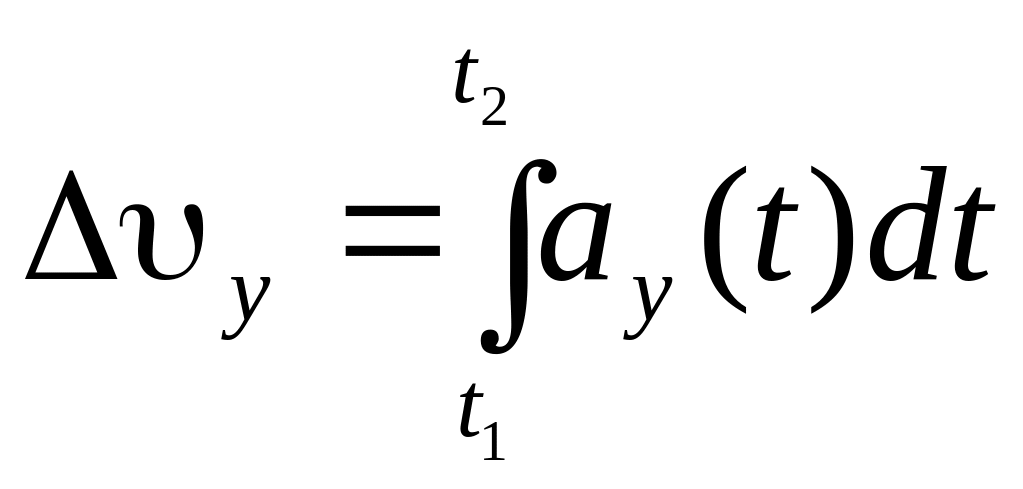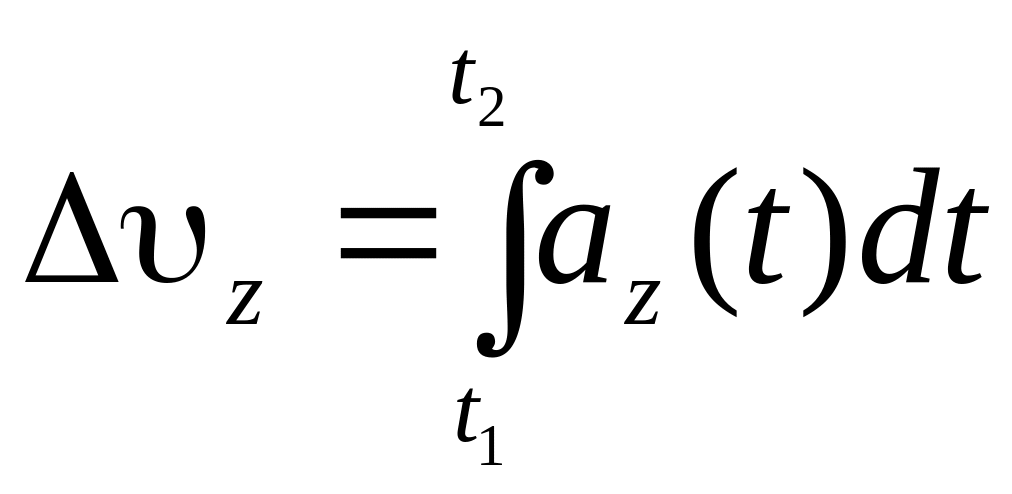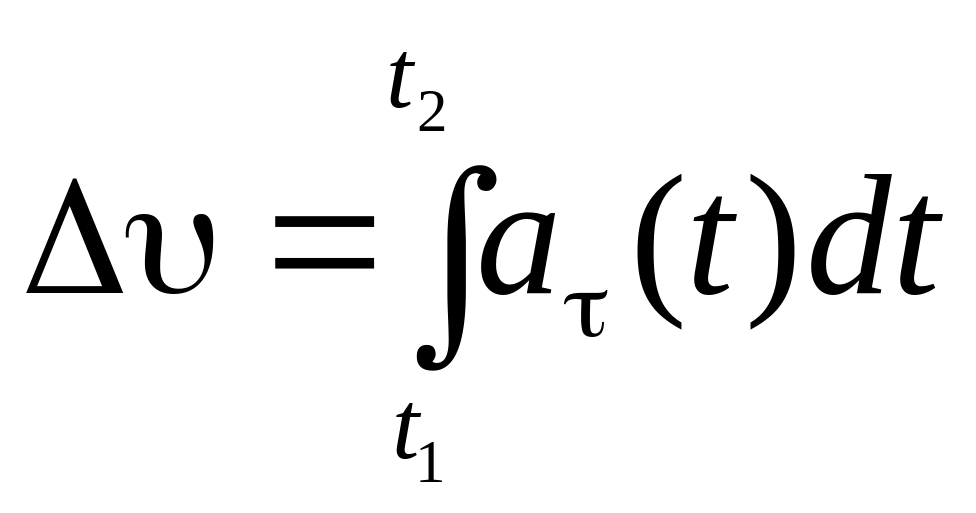Види поступального руху:

1) , - прямолінійний рівномірний рух: .

2) , - прямолінійний рівнозмінний (рівноприскорений або рівносповільнений) рух. Якщо , то:

; ;

3) , - рівномірний рух по колу.

4) , - криволінійний змінний рух.