Приклади розв'язання задач.

Приклад 1. В посудині знаходиться суміш 1 кг кисню і 2 кг гелію за нормальних умов. Знайти, який об’єм займає суміш, її молекулярну вагу, а також густину суміші цих ідеальних газів.

m1 = 1 кг µ1 = 32∙10–3 кг/моль m2 = 2 кг µ2 = 4∙10–3 кг/моль R = 8,31 Дж/(моль∙К) T0 = 273 К p0 = 1,013∙105 Па

V – ? µc – ? ρc – ?

Аналіз і розв’язання

Для суміші двох ідеальних газів справедливий закон Дальтона:

,

де р₁ і р₂ – парціальні тиски, які визначаються з рівняння Менделєєва-Клапейрона

.

; .

де Т₀ – температура суміші, V – об’єм посудини, де знаходяться змішані гази.

Підставляючи в закон Дальтона вирази для p₁ та p₂, отримаємо

.

Оскільки р_с = р₀, то .

Молекулярну вагу суміші визначимо також із рівняння Менделєєва-Клапейрона:

,

тому

.

Відповідно до визначення густини суміші маємо

.

Перевіримо розмірність невідомих фізичних величин:

;

;

.

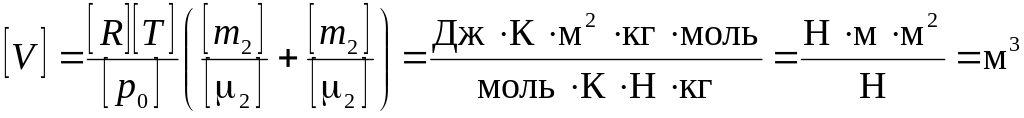Проведемо обчислення невідомих фізичних величин у СІ:

м³;

кг/моль;

кг/м³.

Відповідь: V = 12 м³; µ_c = 5,64∙10^–3 кг/моль; ρ_c = 0,252 кг/м³.

Приклад 2. Визначити число молекул водню, які перетинають за 1 с площадку площею 1 см², розташовану перпендикулярно осі (водень знаходиться за нормальних умов).

µ = 2∙10–3 кг/моль Δt = 1 с ΔS = 1 см2 = 10–4 м2 ρ0 = 1,013∙105 Па T0 = 273 К R = 8,31 Дж/(мольК) k = 1,38∙10–23 Дж/К

n1 – ? n2 – ?

Аналіз і розв’язання

Наведемо два способи розв’язування цієї задачі.

І спосіб. Враховуючи, що в газі немає переважних напрямків руху молекул, приймемо, що 1/3 всіх молекул рухається вздовж осі ОX, 1/3 – вздовж осі ОY і 1/3 – вздовж осі ОZ. Відповідно, в додатному напрямі осі ОX рухається 1/6 всіх молекул. Далі зробимо припущення, що швидкості всіх молекул однакові й дорівнюють середній швидкості v. Тоді шукане число молекул складатиме

,

де n₀ – концентрація молекул (їх число в одиниці об’єму), яка визначається за формулою

,

де k – стала Больцмана.

Перевіримо розмірність невідомої величини:

.

Середня арифметична швидкість може бути знайдена за формулою

.

Підставляючи, отримаємо

.

Проведемо обчислення в СІ:

.

ІІ спосіб. В першому випадку вважалось, що молекули рухаються з однаковою за модулем швидкістю, яка дорівнює середній арифметичній. Однак молекули, розподілені за компонентами швидкостей згідно з законом Максвелла, який для одновимірного випадку легко одержати із розподілу

.

Отже, число молекул, яке перетинає площадку ΔS = 1 см² за час Δt = 1 с, знайдемо зі співвідношення

,

де .

Враховуючи, що , одержимо

Таким чином, одержані вирази для n₁ і n₂ різко відрізняються.

Відповідь: n₁ 7,62∙10²³; n₂ 11,1∙10²³.

Приклад 3. Кисень, маса якого 2 кг, знаходиться в закритій посудині об’ємом V₁ = 1 м³ під тиском р₁ = 2∙10⁵ Н/м². Газ спочатку нагрівають при сталому тиску до об’єму V₂ = 3 м³, а потім при сталому об’ємі до тиску р₃ = 5∙10⁵ Н/м². Обчислити зміну внутрішньої енергії газу, виконану ним роботу і теплоту, яка була передана газу.

m = 2 кг µ = 32∙10–3 кг/моль i = 5 p1 = 2∙105 Па V1 = 1 м3 V2 = 3 м3 p3 = 5∙105 Па R = 8,31 Дж/(мольК)

ΔU – ? A – ? Q – ?

Аналіз і розв’язання

Питома теплоємність газу при сталому об’ємі визначається за формулою , де і – число степенів вільності молекул газу (для двохатомних молекул кисню і = 5: три степені вільності поступального та дві степені – обертального руху). Зміна внутрішньої енергії газу

,

де – різниця температур газу в кінцевому (третьому) і початковому станах.

Початкову і кінцеву температури газу знайдемо з рівняння Менделєєва-Клапейрона :

.

Робота по розширенню газу при сталому тиску виражається формулою

.

Робота газу, який нагрівається при сталих тиску й об’ємі, дорівнює нулю: А₂ = 0.

Отже, повна робота, виконувана газом: .

Відповідно до першого закону термодинаміки, теплота Q, передана газу, дорівнює сумі зміни внутрішньої енергії ΔU і роботи А. Обчислимо всі температури:

К;

К;

К.

Враховуючи значення температур, знаходимо роботу:

Дж.

Перевіримо розмірність роботи:

Знайдемо зміну внутрішньої енергії:

 Дж.

Перевіримо розмірність :

Теплота, яка була передана газу,

Дж.

Відповідь: ΔU = 3,24∙10⁶ Дж; A = 4∙10⁵ Дж; Q = 3,64∙10⁶ Дж.