Рівняння стану ідеального газу.

Рівнянням стану термодинамічної системи називається рівняння, яке зв’язує тиск р, об’єм V і температуру Т термодинамічної системи, яка знаходиться в стані термодинамічної рівноваги:

,

де кожна зі змінних є функцією двох інших.

Припустимо, що деяка маса газу знаходиться в стані 1, при цьому її об’єм V₁, тиск р₁, температура Т₁. Ця ж маса газу в іншому довільному стані характеризується параметрами р₂, V₂, Т₂. Перехід зі стану 1 в стан 2 здійснюється послідовно ізотермічним (1–1) і ізохорним (1–2) процесами (рис.2.1).

З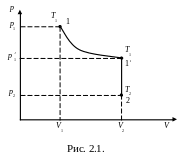 апишемо для визначених станів рівняння за законами Бойля-Маріотта і Гей-Люссака.

, .

Виключаючи , отримаємо рівняння стану ідеального газу: для даної маси ідеального газу відношення добутку тиску та об’єму до термодинамічної температури є стала величина (рівняння Клапейрона)

чи .

За однакових тиску р та температурі Т молі всіх газів займають однаковий молярний об’єм , згідно з законом Авогадро. Рівняння стану для моля ідеального газу: , де константа R = 8,31 Дж/(моль·К) – називається універсальною газовою сталою.

Об’єм газу маси m: .

Для довільної маси m газу рівняння стану ідеального газу, рівняння Менделєєва-Клапейрона має вигляд:

.

Використовуючи сталу Больцмана: Дж/К, рівняння стану можна записати у вигляді:

,

де – концентрація молекул – кількість молекул в одиниці об’єму.

Таким чином:

1) тиск ідеального газу при даній температурі прямо пропорційний концентрації його молекул,

2) при однакових температурі і тиску всі гази налічують в одиниці об’єму однакове число молекул.

Кількість молекул, яка налічуються в 1м³ газу за нормальних умов, називається числом Лошмідта:

1/м³.

Основне рівняння молекулярно-кінетичної теорії ідеальних газів.

Припустимо, що в посудині об’ємом V знаходиться ідеальний газ масою m, який складається із N молекул масою m₀, які рухаються з однаковими швидкостями υ. Концентрація молекул в газі за визначенням .

Якщо при зіткненні зі стінками за час Δt елементарній площадці ΔS стінці посудини передається імпульс ΔР, то тиск газу, який він створює на стінку посудини .

При кожному зіткненні молекула, яка рухається перпендикулярно стінці, передає їй імпульс 2m₀υ. В середньому в напрямку до стінки рухається 1/6 частина всіх молекул. (Якщо розглянути три взаємно перпендикулярні осі, то в середньому тільки 1/3 молекул рухається вздовж однієї з осей і тільки половина із них – 1/6 вздовж даного напрямку). За час Δt площадки ΔS досягне 1/6nΔSυΔt молекул і передадуть їй імпульс .

Тиск, який створює газ на стінку посудини: .

Якщо газ об’ємом V вміщає N молекул, які рухаються зі швидкостями υ₁, υ₂, …, υ_N, то доцільно розглядати середню квадратичну швидкість, яка визначається як

,

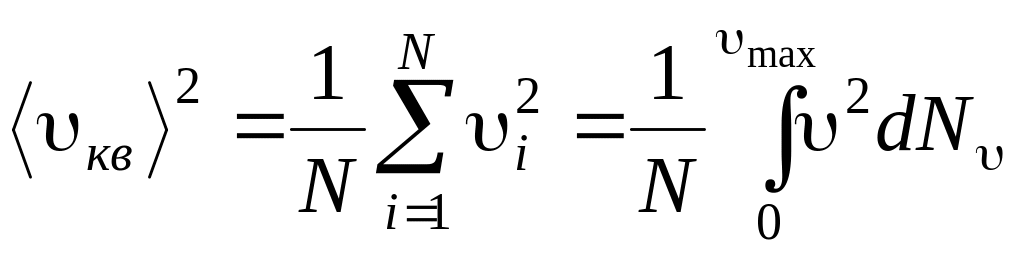і характеризує всю сукупність молекул газу.

Основне рівняння молекулярно-кінетичної теорії ідеальних газів:

.

Інші варіанти запису цього рівняння з урахуванням співвідношень

; ;

; ,

де Е – сумарна кінетична енергія поступального руху всіх молекул газу, – молярний об’єм, μ – молярна маса.

Використовуючи рівняння Клапейрона-Менделєєва, отримаємо , звідки середньоквадратична швидкість молекул ідеального газу:

.

Середня кінетична енергія поступального руху однієї молекули ідеального газу:

.

Звідси витікає, що при Т = 0 К – зупиняється рух молекул газу.

Молекулярно-кінетичне тлумачення температури: термодинамічна температура – міра середньої кінетичної енергії поступального руху молекул газу.