Зіткнення.

Удар (зіткнення} — зіткнення двох або більш тіл, при якому взаємодія триває дуже короткий час.

Центральний удар — удар при якому тіла до удару рухаються по прямій, що проходить через їх центри мас.

Абсолютно пружний удар — зіткнення двох тіл, в результаті якого в обох взаємодіючих тілах не залишається ніяких деформацій і вся кінетична енергія, якою володіли тіла до удару, після удару знову перетворюється на кінетичну енергію. Виконуються закони збереження імпульсу і збереження механічної енергії.

Позначимо швидкості двох пружних куль масами і до удару через і , після удару — через і . Розглянемо прямий центральний удар. Закони збереження:

; .

Звідси:

;

Абсолютно непружний удар — зіткнення двох тіл, в результаті якого тіла деформуються і об'єднуються, рухаючись далі як єдине тіло.

; .

При ;

При недружньому ударі не виконується закон збереження механічної енергії –унаслідок деформації частина кінетичної енергії переходить у внутрішню енергію тіл. Це зменшення кінетичної енергії дорівнює

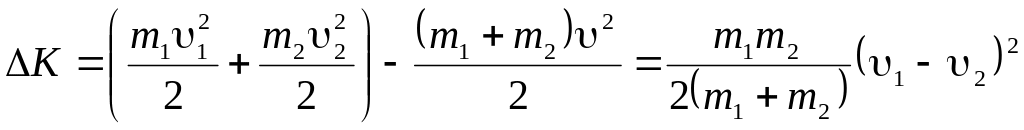
Якщо тіло, що ударяється, було спочатку нерухомо ( ), то:

; .

Якщо , то і

Поле сил тяжіння.

Закон всесвітнього тяжіння: між будь-якими двома матеріальними точками діє сила взаємного тяжіння, прямопропорційна добутку мас цих точок і обернено пропорційна квадрату відстані між ними:

.

де G = 6,6710^ Нм^кг^ - гравітаційна стала.

Ця сила називається гравітаційною, або силою всесвітнього тяжіння. Гравітаційні сили тяжіння завжди є силами притягування і направлені уподовж прямій, що проходить через взаємодіючі тіла.

Гравітаційна взаємодія між тілами здійснюється за допомогою поля тяжіння, або гравітаційного поля.

На прикладі гравітаційного поля розглянемо поняття напруженості поля і потенціалу поля.

Напруженість поля тяжіння в деякій точці це фізична величина, що дорівнює силі діючої з боку поля на тіло одиничної маси в цій точці. Напруженість є векторною силовою характеристикою поля тяжіння

.

У гравітаційному полі Землі , звідки

,

де R₃ - радіус Землі, маса якої М, h - відстань від центру тяжіння тіла до поверхні Землі. При переміщенні тіла масою m на відстань dR поле тяжіння здійснює роботу (знак мінус тому, що сила і переміщення протилежно направленні).

При переміщенні тіла з відстані R₁ до відстані R₂:

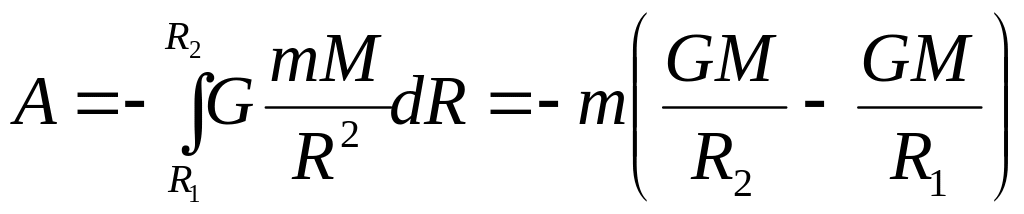
Робота не залежить від траєкторії переміщення, а визначається тільки початковим і кінцевим положеннями тіла.

Отже, сили тяжіння консервативні, а поле тяжіння є потенційним. Робота консервативних сил дорівнює зміні потенціальної енергії системи із зворотним знаком . Взявши нульовий рівень потенціальної енергії на нескінченній відстані отримаємо потенціальну енергію тіла масою m на відстані R від тіла масою M

Для будь-якого потенційного поля можна визначити скалярну енергетичну характеристику поля — потенціал.

Потенціалом поля тяжіння в даній точці поля називається скалярна величина, що дорівнює потенціальній енергії тіла одиничної маси в цій точці

.

Розглянемо зв'язок між потенціалом поля тяжіння і його напруженістю:

; ;

, або .

У загальному випадку для будь-якого потенційного поля між напруженістю і потенціалом існує зв'язок

.

Ця формула є слідством співвідношення .