2. Перемена порядка интегрирования.

Если область  является простой как вида 1), так и вида 2), то применимы обе формулы ( 5) и ( 6), следовательно,

Иными словами, повторное интегрирование не зависит от порядка интегрирования. Этим обстоятельством часто пользуются при вычислении двойного интеграла, выбирая ту из двух формул, которая приводит к более простым выкладкам.

В качестве упражнения на расстановку пределов интегрирования полезна задача о перемене порядка интегрирования в повторном интеграле

Прежде всего, следует начертить область интегрирования , которая находится в полосе между прямыми x = a и x = b и ограничена снизу линией y = ₁(x), а сверху – линией y = ₂(x). Затем область  проектируют на ось Oy и находят уравнения прямых y = c и y = d, ограничивающих снизу и сверху полосу, в которой расположена область ; затем находят левую границу области  х = ₁(y) и правую x = ₂(y). Если какая-либо из этих границ состоит из двух или большего числа линий, записанных разными уравнениями, то область  приходится разбивать на части, а интеграл – на сумму интегралов по этим частям.

Аналогично, если требуется переменить порядок интегрирования в повторном интеграле

то, спроектировав область  на ось Ox, находят уравнения прямых x = a и x = b, нижнюю границу области  y = ₁(x) и верхнюю y = ₂(x).

Иногда область  приходится разбивать на части, а интеграл – на сумму интегралов по этим частям.

Пример 7.

В двойном интеграле расставить пределы для одного и другого порядка интегрирования по области , ограниченной прямыми x =0, x = 1, y = 1 и кривой Область  (рис. 9) находится в полосе между прямыми x = 0 и x = 1. Нижняя граница – дуга окружности , верхняя – прямая y = 1. Следовательно,

.

Область  проектируется на ось Oy в отрезок [-1,1]. Левая граница области имеет уравнение , т.е. при –1  y  0 и x = 0 при 0  y  1. Правая граница x = 1. Разбивая область на две части ₁ и ₂, а интеграл - на сумму двух интегралов, получим:

Пример 8.

В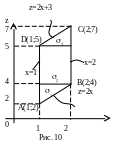 двойном интеграле расставить пределы для того и другого порядка интегрирования по области , которая является параллелограммом с вершинами в точках А(1;2), В(2;4), С(2;7), D(1;5).

Н

x

айдем уравнения границ области  (рис. 10): для АВ z =2x, для BC x = 2, для CD z = 2x + 3, для DA x = 1, т.к. область  лежит в плоскости xOz. Область  находится в полосе между прямыми x = 1 и x = 2 и ограничена снизу прямой z = 2x, а сверху прямой z = 2x + 3, поэтому

Для того, чтобы расставить пределы в другом порядке, разбиваем область  на три части (см. рис. 10):

и тогда получим:

Пример 9.

И

зменить порядок интегрирования в повторном интеграле

Область  (рис.11) расположена в плоскости yOz и между прямыми y = 0 и y = 1. Ее нижняя граница z = y, верхняя . Спроектируем область  на ось Oz. В результате получим отрезок Левой границей области  является прямая y = 0, правой на участке [0;1] – прямая y = z, а на участке – дуга окружности .

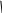
z=y

Поэтому область  следует разбить на две части (₁ и ₂), а интеграл – на сумму интегралов:

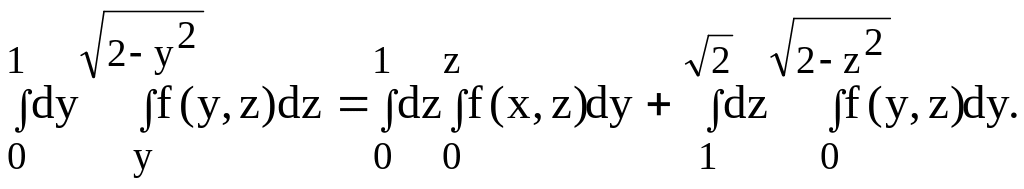
Пример 10.

В двойном интеграле расставить двумя способами пределы интегрирования по области , определенной неравенствами: , y +1  0, -1  x  3.

Область интегрирования , ограниченная верхней ветвью параболы y² = x + 1, горизонтальной прямой y = -1 и двумя вертикальными прямыми x = -1 и x = 3, изображена на рис. 12.

В первом случае внутренний интеграл берется при условии x = const. Прямая x = const при входе в область  пересекает прямую y =-1, а при выходе из  – параболу , поэтому (см.формулу (5)):

Во втором случае переменная y принимает значения –1  y  2 (координаты точки пересечения параболы и прямой x = 3 будут x = 3; ). Внутренний интеграл вычисляется при условии y = const. Прямая y = const при выходе из области  пересекает прямую x = 3, а при входе – либо прямую x = -1 (если –1  y < 0), либо параболу x=y²–1 (если 0  y  2), т.е. левая граница состоит из двух различных кривых. Таким образом, область  разбивается на две части: ₁ и ₂ прямой y = 0, а интеграл представляется в виде суммы двух интегралов:

Пример 11.

И зобразить область интегрирования и поменять порядок интегрирования в интеграле

Из записи интеграла видно, что область интегрирования разбита на 3 области: первая ограничена линиями: x = -2, x = 0, y = -2, y = 2; вторая – линиями: x = 0, x = 4, y = -2, y = - ; третья – линиями: x = 0, x = 4, y = , y = 2 (рис. 13).

О

0

бъединяя эти области, мы получим правильную в направлении оси Ох область. Отдельные участки правой границы этой области задаются по-разному: y = и y = - , однако, ее можно задать и одним уравнением x = y². Тогда, расставляя пределы интегрирования, в соответствии с формулой ( 6) получим: