
- •IV. Общая схема построения интегралов.
- •IV. А Двойные и тройные интегралы.
- •1. Построение и вычисление двойных интегралов в декартовых прямоугольных координатах.
- •Измельчая дробление, ищем предел для (1), т.Е.
- •2. Перемена порядка интегрирования.
- •3. Замена переменных в двойном интеграле. Вычисление двойных интегралов в полярных координатах.
- •Пример 16.
- •4. Приложения двойного интеграла
- •Пример 19.
- •Пример 26.
- •Пример 27.
- •1. Построение. Вычисление тройных интегралов в декартовых прямоугольных координатах.
- •Пример 1.
- •Пример 2.
- •2. Вычисление тройных интегралов в криволинейных координатах.
- •3. Приложения тройного интеграла.
- •Задачи для самостоятельного решения.
- •IV. В Криволинейные и поверхностные интегралы.
- •1. Криволинейные интегралы первого рода (по длине дуги) – кипр.
- •2. Криволинейные интегралы второго рода (по координатам) – кивр.
- •3. Формула Грина и ее применение.
- •4. Условия независимости криволинейных интегралов от формы пути интегрирования ( условия нпи).
- •5. Приложения криволинейных интегралов.
- •1. Поверхностные интегралы первого рода (по площади поверхности).
- •2. Односторонние и двусторонние поверхности.
- •Связь между поверхностными интегралами первого и второго рода.
- •Вычисление пивр
- •3. Формула Остроградского – (Гаусса).
- •4. Формула Стокса.
- •Задачи для самостоятельного решения.
- •В задачах 115 117 вычислить заданный криволинейный интеграл.
В задачах 115 117 вычислить заданный криволинейный интеграл.
![]() один виток винтовой
линии
один виток винтовой
линии
![]() от точки А (1;0;0) до точки В (1;0;4).
от точки А (1;0;0) до точки В (1;0;4).
116.
![]() вдоль дуги кубической параболы
вдоль дуги кубической параболы
![]() от точки А (1;1) до В (2;8).
от точки А (1;1) до В (2;8).
117.
![]() окружность, образованная пересечением
поверхностей
окружность, образованная пересечением
поверхностей
![]()
118. Найти массу
дуги кривой
![]() от
точки А с абсциссой х = 1 до В с абсциссой
х = 2, если плотность дуги
от
точки А с абсциссой х = 1 до В с абсциссой
х = 2, если плотность дуги
![]() .
.
119.
![]() от
от
![]() .
.
120.
![]() до
до
![]() .
.
121.
![]() .
.
122.
![]() .
.
123.
![]() .
.
124.
![]() .
.
125.
![]() .
.
126.
![]() от А (–2;0) до В (2;0).
от А (–2;0) до В (2;0).
127.
![]() от А(0;–1) до В(1;–2).
от А(0;–1) до В(1;–2).
128.
![]() .
.
В задачах 129 138 вычислить поверхностный интеграл. Сделать чертеж поверхности.
129.
![]() где
где
![]() –
часть поверхности z
= 12 – 3x
– 4y,
ограниченная координатными плоскостями.
–
часть поверхности z
= 12 – 3x
– 4y,
ограниченная координатными плоскостями.
130.
![]() ограниченная
координат-
ограниченная
координат-
ными плоскостями
![]() .
(При вычислении двойного интеграла
перейти к полярным координатам).
.
(При вычислении двойного интеграла
перейти к полярным координатам).
131.
![]()
ограниченная поверхностями y = x, x = 0 и z = 0.
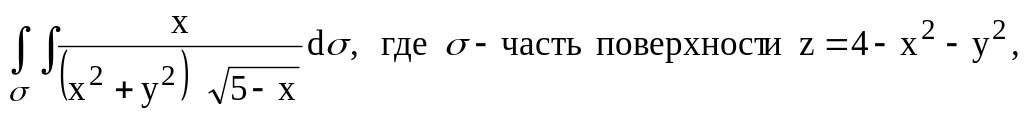 лежащая
между поверхностями х = 0, z
= 0 и у = 1 (у
1). (При вычислении двойного интеграла
перейти к полярным координатам)
лежащая
между поверхностями х = 0, z
= 0 и у = 1 (у
1). (При вычислении двойного интеграла
перейти к полярным координатам)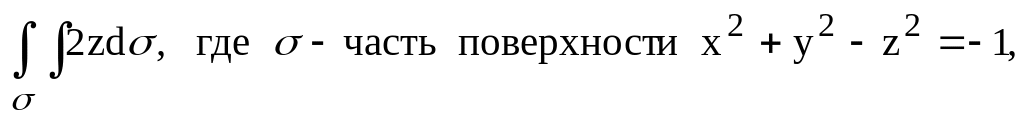 ограниченная
поверхностью
ограниченная
поверхностью
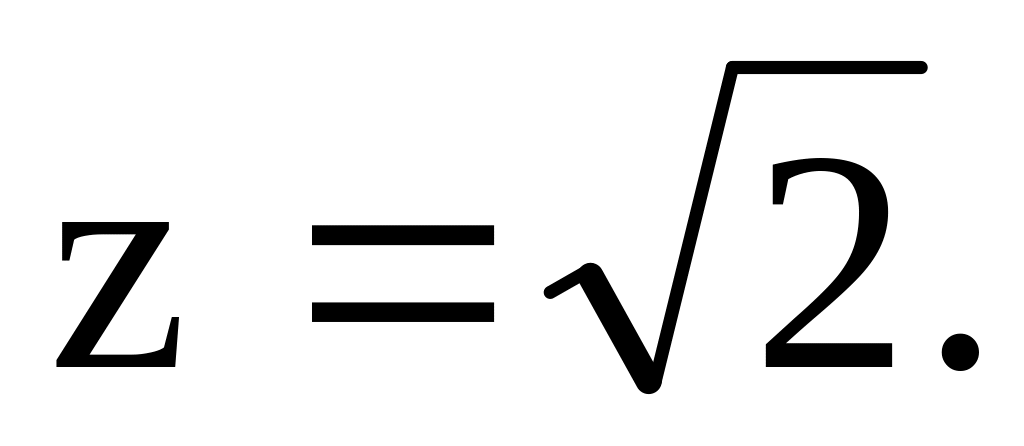 (При вычислении двойного интеграла
перейти к полярным координатам).
(При вычислении двойного интеграла
перейти к полярным координатам).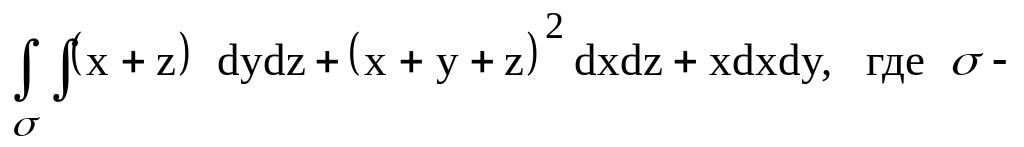 верхняя
сторона части поверхности x
+ y
+ z
= 1, ограниченной координатными
плоскостями.
верхняя
сторона части поверхности x
+ y
+ z
= 1, ограниченной координатными
плоскостями.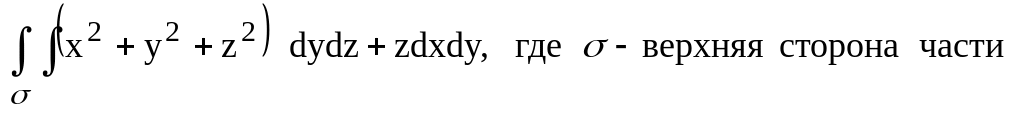 поверхности
поверхности
 .
При вычислении двойных интегралов
перейти к полярным координатам.
.
При вычислении двойных интегралов
перейти к полярным координатам.
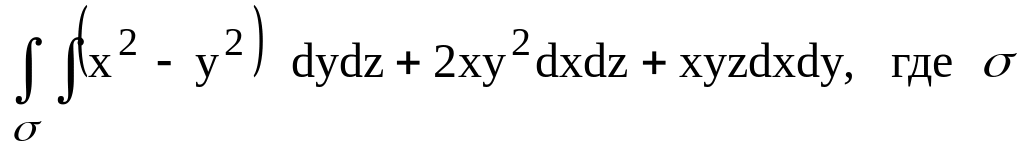 – часть поверхности
– часть поверхности
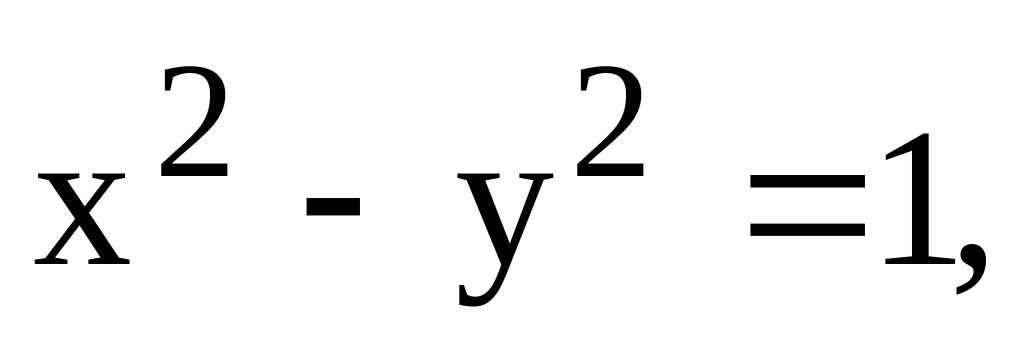 ограниченная поверхностями
ограниченная поверхностями
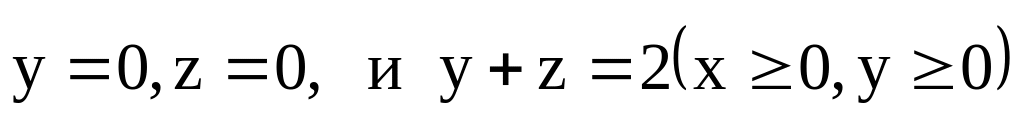 .
Нормаль к поверхности образует острый
угол с осью 0х.
.
Нормаль к поверхности образует острый
угол с осью 0х.
 внешняя
сторона части поверхности
внешняя
сторона части поверхности
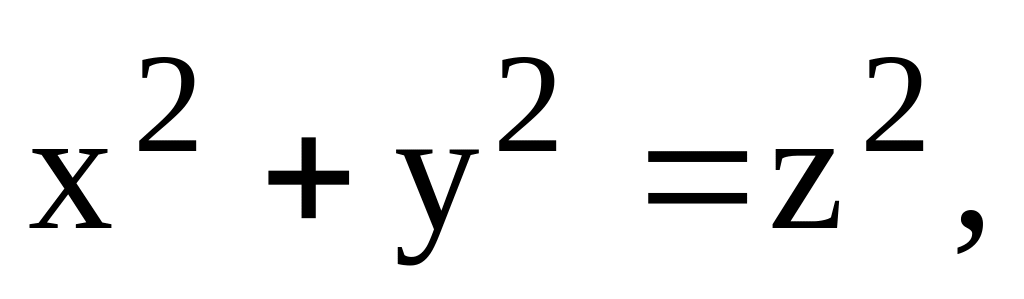 ограниченной поверхностями x
= 0, y
= 0 и z
= 1 (x
0,y
0). ( При вычислении двойного интеграла
по области
ограниченной поверхностями x
= 0, y
= 0 и z
= 1 (x
0,y
0). ( При вычислении двойного интеграла
по области
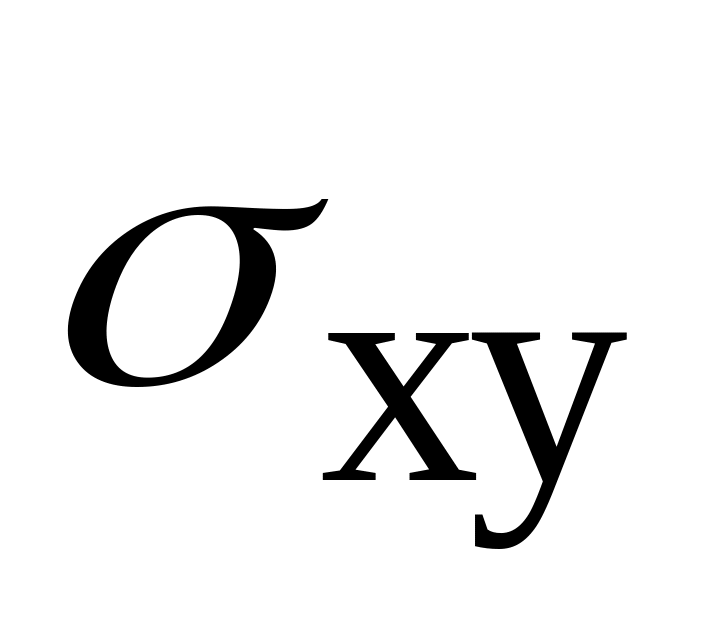 перейти к полярным координатам).
перейти к полярным координатам).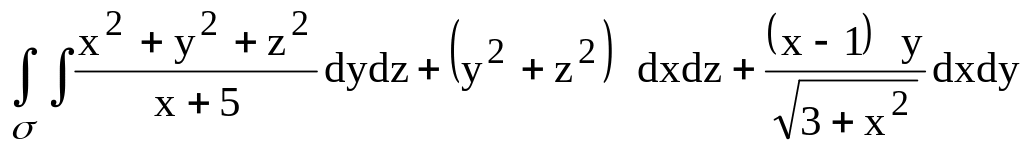 ,
где
–
верхняя сторона части поверхности
,
где
–
верхняя сторона части поверхности
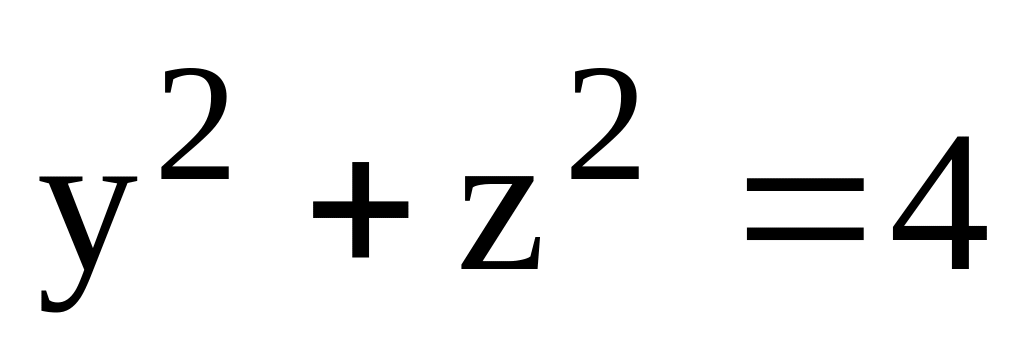 ,
ограниченной поверхностями х=0, у=0 и
х+у=1.
,
ограниченной поверхностями х=0, у=0 и
х+у=1.
В задачах 139 312 вычислить данные криволинейные интегралы.
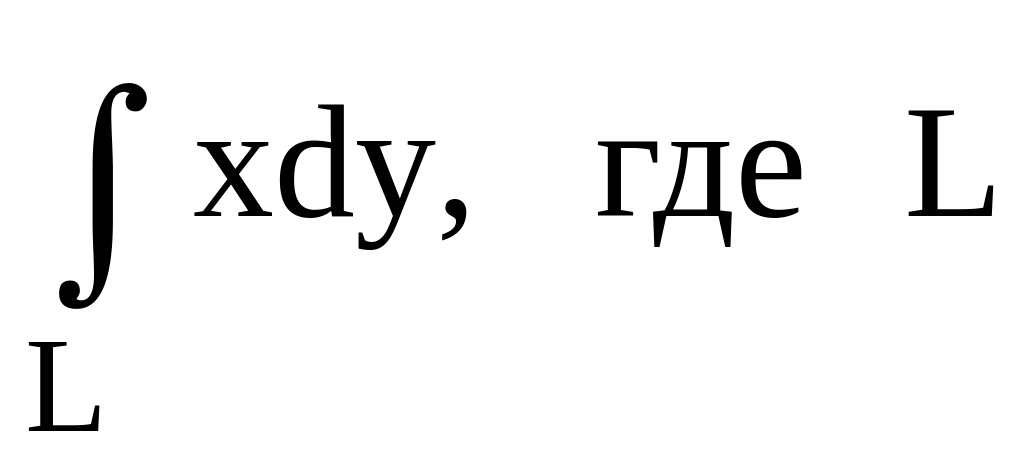 –
контур треугольника,
образованного осями координат и прямой
–
контур треугольника,
образованного осями координат и прямой
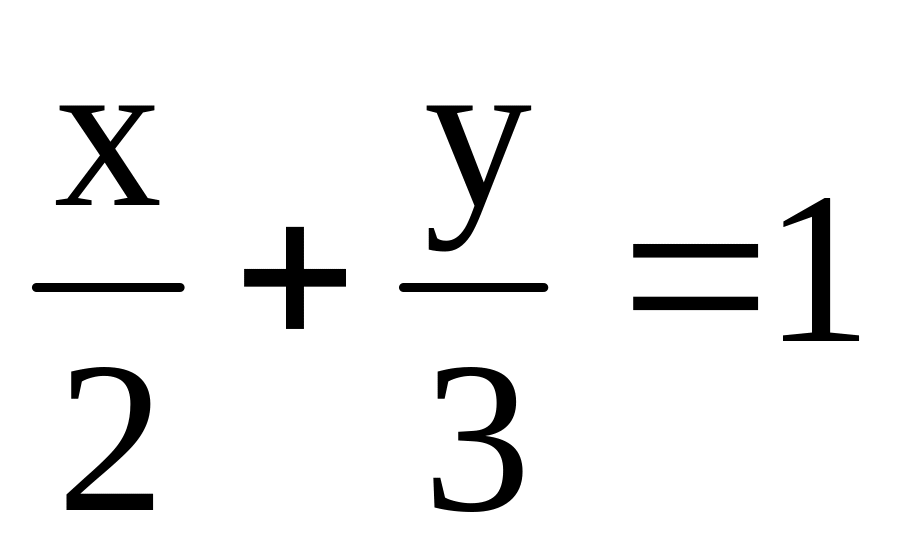 в положительном направлении.
в положительном направлении. вдоль
кривой
вдоль
кривой
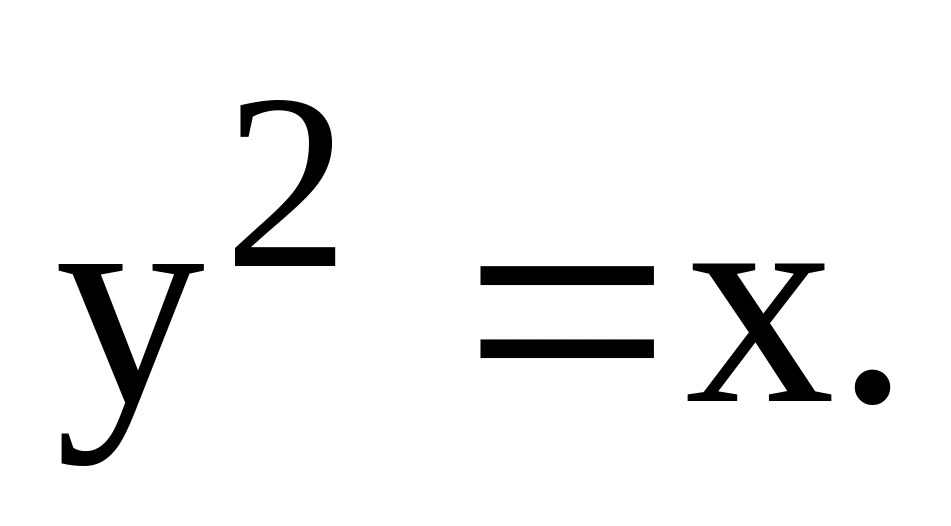
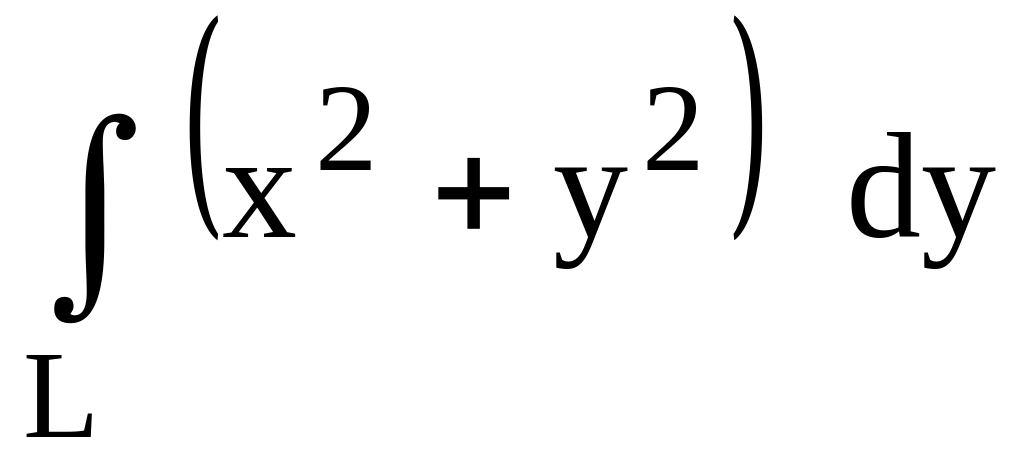 ,
где L
– контур прямоугольника, образованного
прямыми
х = 1, х = 3, у = 1, у = 5 в положительном
направлении.
,
где L
– контур прямоугольника, образованного
прямыми
х = 1, х = 3, у = 1, у = 5 в положительном
направлении.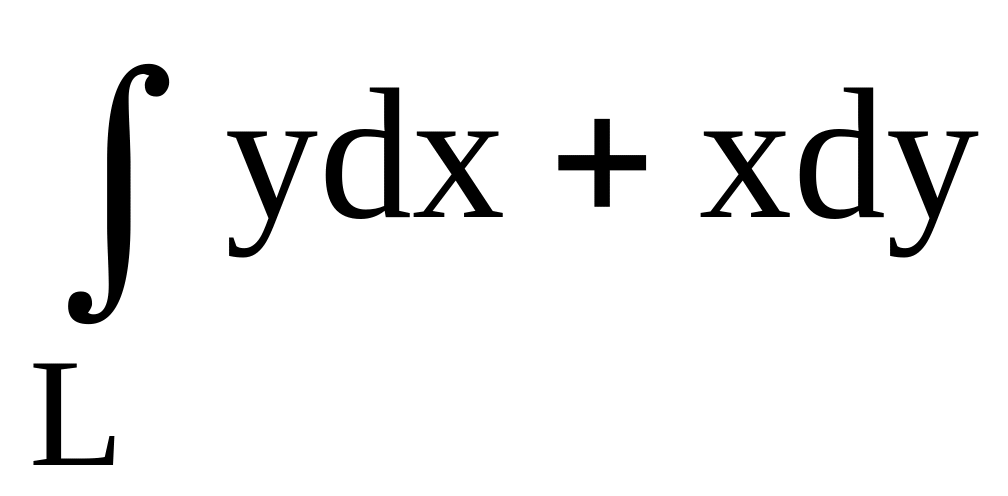 ,
где L
– четверть окружности x
= r
cos
t,
y=r
sin
t
от t=0
до
,
где L
– четверть окружности x
= r
cos
t,
y=r
sin
t
от t=0
до
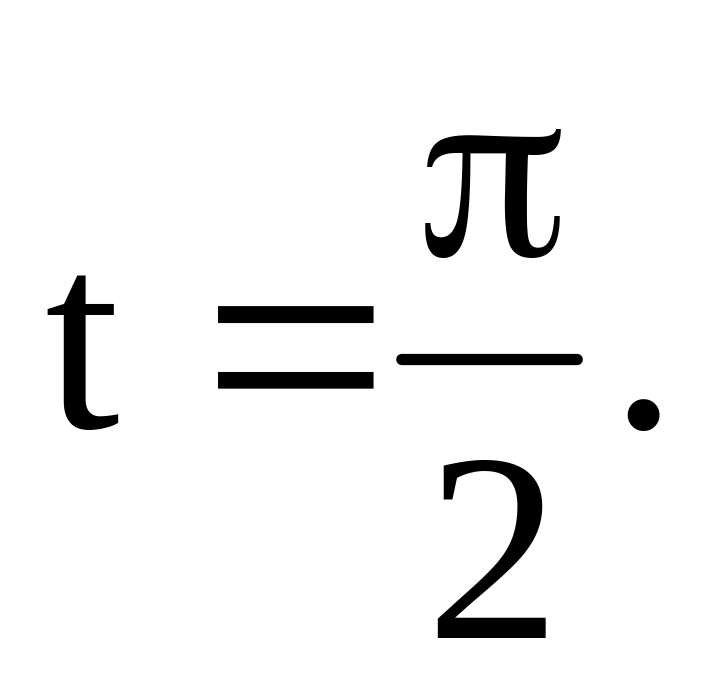
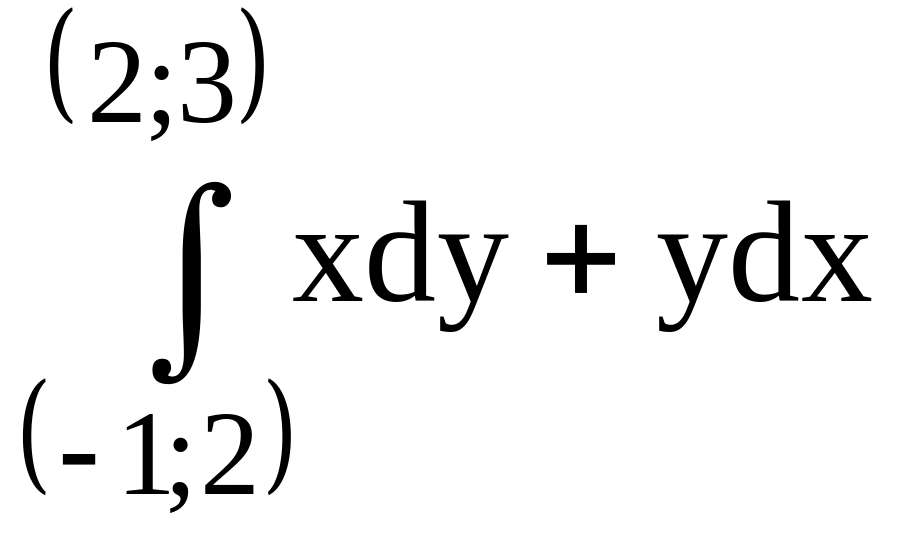 вдоль
прямой, соединяющей точки (–1;2) и (2;3).
вдоль
прямой, соединяющей точки (–1;2) и (2;3).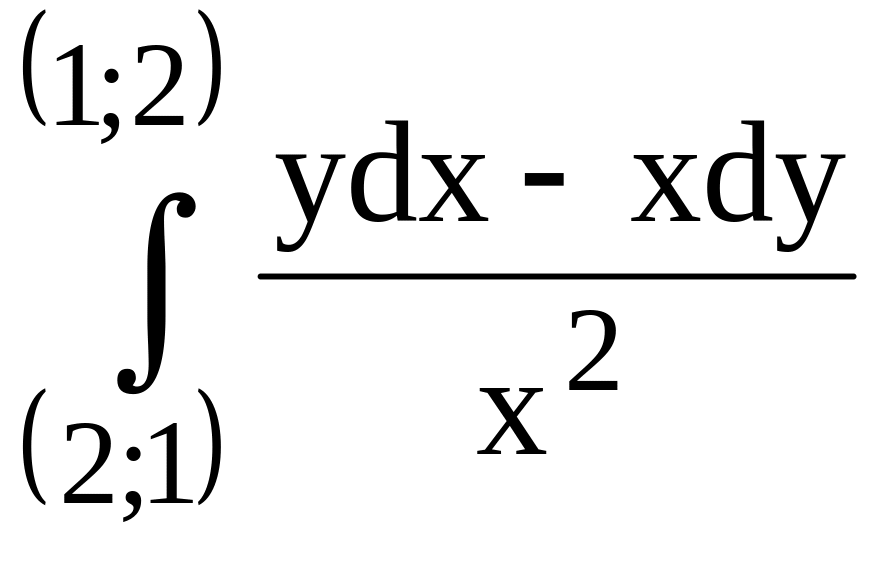 вдоль прямой,
соединяющей точки (2;1) и (1;2).
вдоль прямой,
соединяющей точки (2;1) и (1;2).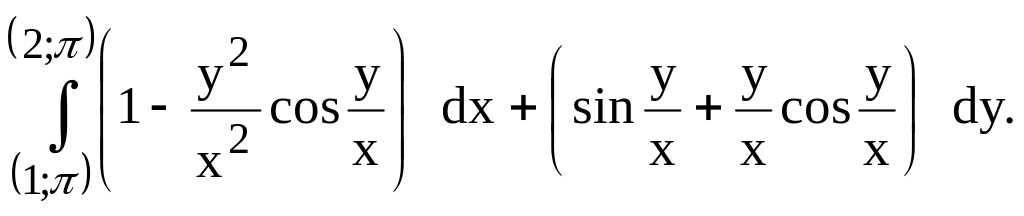
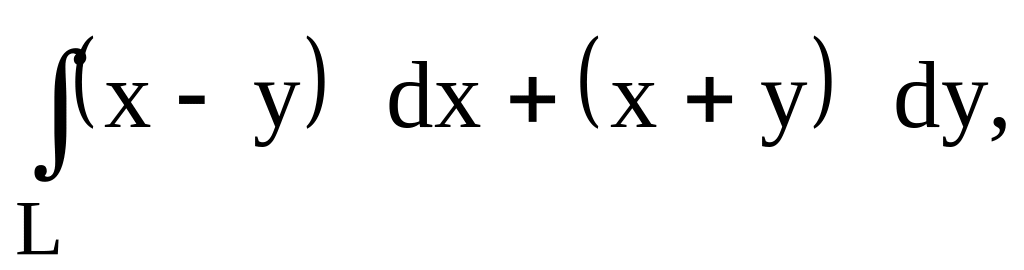 где
L
– отрезок прямой, соединяющей точки А
(2;3) и В (3;5).
где
L
– отрезок прямой, соединяющей точки А
(2;3) и В (3;5).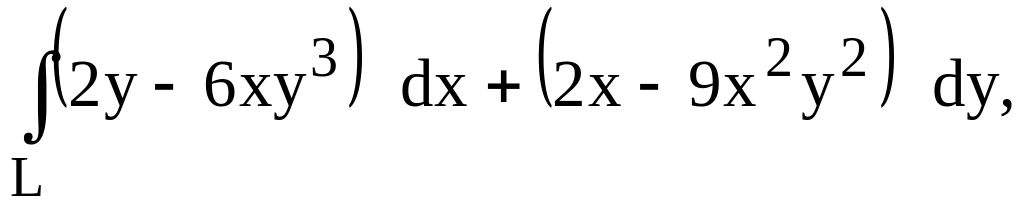 где
L
– дуга параболы
где
L
– дуга параболы
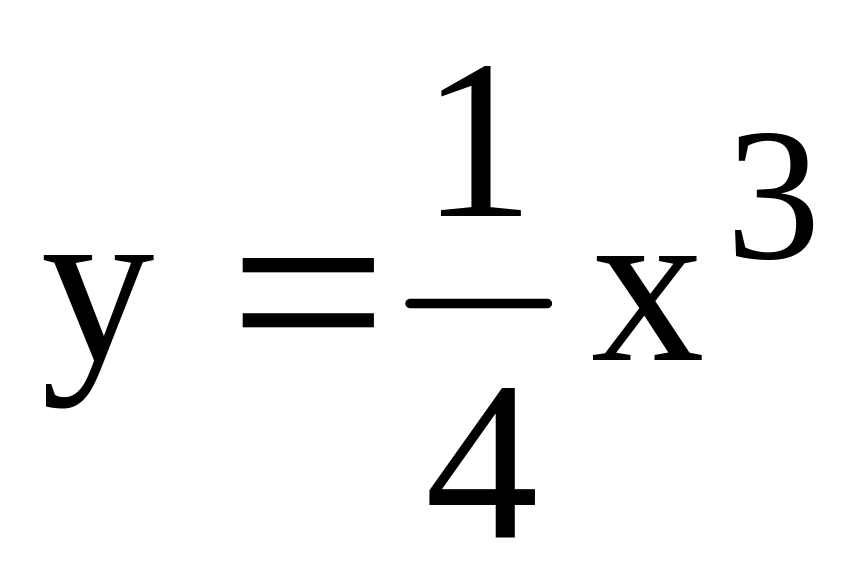 от точки О (0;0) до точки А (2;2).
от точки О (0;0) до точки А (2;2).
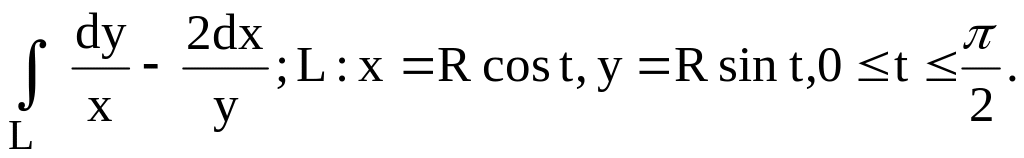
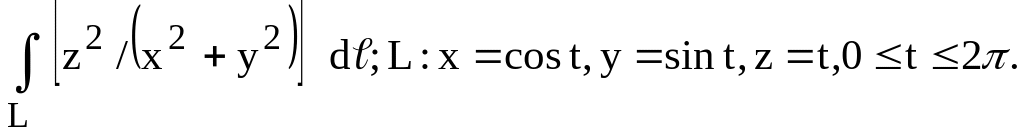
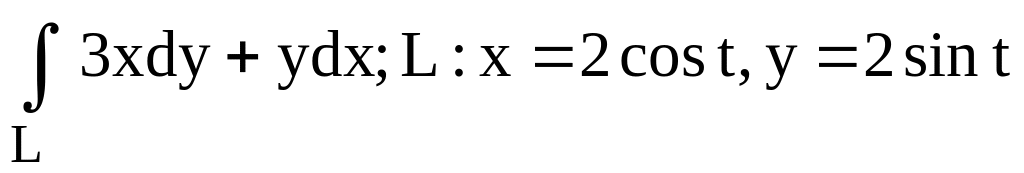 (в
первом квадранте).
(в
первом квадранте).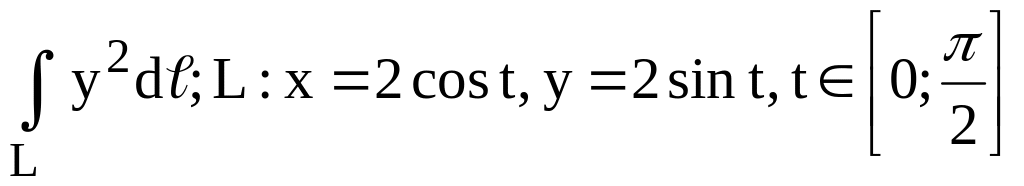 .
.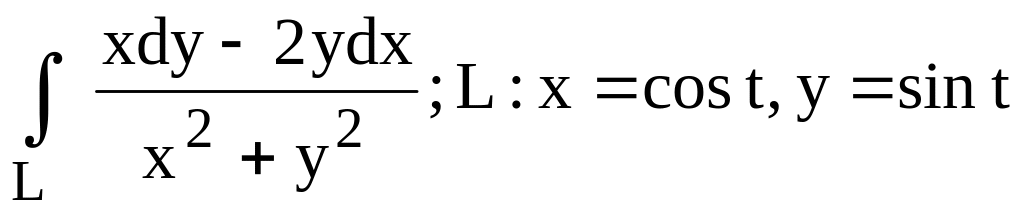 (
в первом квадранте).
(
в первом квадранте).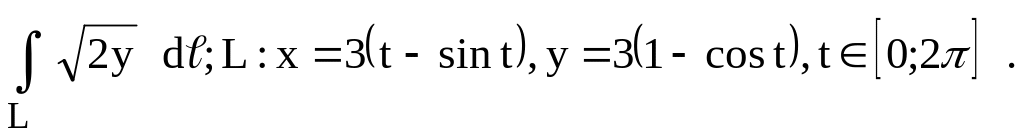

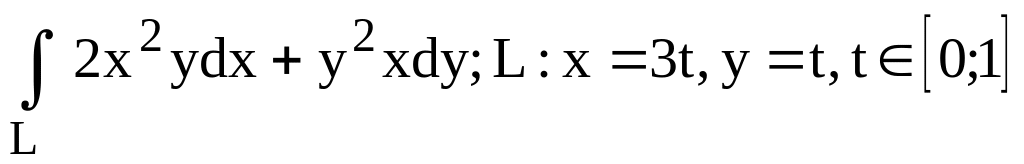 .
.
157.
![]() .
.
158.
![]() дуга
кривой
дуга
кривой
![]() от
(0;0) до (1;1).
от
(0;0) до (1;1).
159.
![]() .
.
160.
![]() отрезок прямой от (0;0) до (1;3).
отрезок прямой от (0;0) до (1;3).
161.
![]() дуга кривой
дуга кривой
![]() проходимая по часовой стрелке.
проходимая по часовой стрелке.
162.
![]() до (1;е).
до (1;е).
163.
![]() .
.
164.
![]()
165.
![]() .
.
166.
![]() прямая
от (1;3) до (2;5).
прямая
от (1;3) до (2;5).
167.
![]() в положительном направлении. Использовать
формулу Грина – Римана.
в положительном направлении. Использовать
формулу Грина – Римана.
168.
![]() .
.
169.![]() в положительном направлении. Использовать
формулу Грина – Римана.
в положительном направлении. Использовать
формулу Грина – Римана.
170.
![]() контур
треугольника АВС, где А (0;0),
контур
треугольника АВС, где А (0;0),
В (1;0), С (1;1). Использовать формулу Грина – Римана.
171.
![]() прямая от (1;3) до (4;5).
прямая от (1;3) до (4;5).
172.
![]()
Использовать формулу Грина – Римана.
173.
![]() от (1;1) до (2;2).
от (1;1) до (2;2).
174.
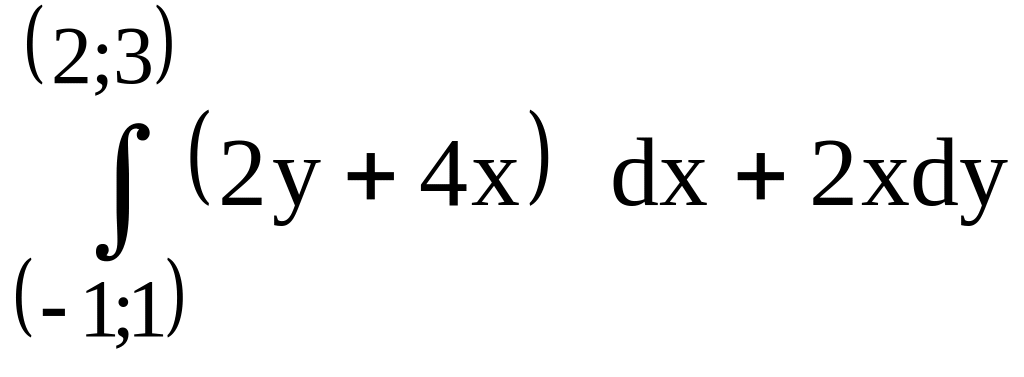 (
предварительно убедиться, что он не
зависит от пути
интегрирования).
(
предварительно убедиться, что он не
зависит от пути
интегрирования).
175.
![]() отрезок прямой от (1;1;1) до (3;2;4).
отрезок прямой от (1;1;1) до (3;2;4).
176.
 (предварительно убедиться, что
он не зависит от пути интегрирования).
(предварительно убедиться, что
он не зависит от пути интегрирования).
177.
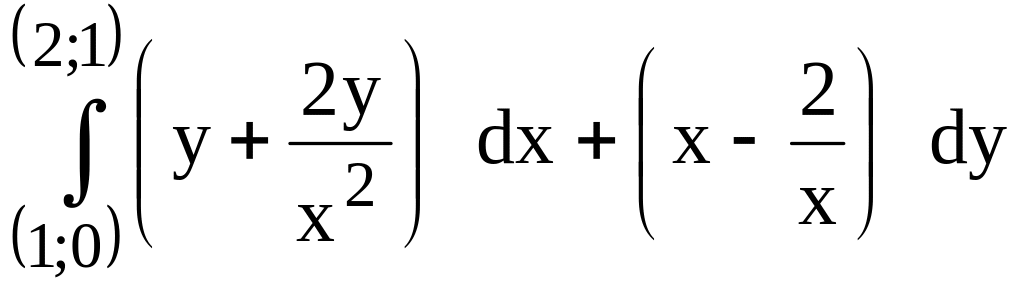 ( предварительно убедиться, что он не
зависит от пути интегрирования).
( предварительно убедиться, что он не
зависит от пути интегрирования).
178.
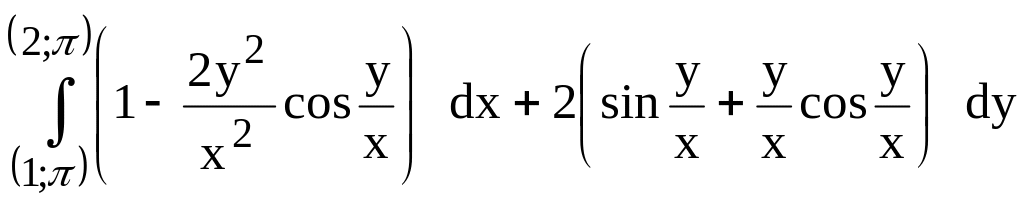 (предварительно
убедиться, что он не зависит от пути
интегрирования).
(предварительно
убедиться, что он не зависит от пути
интегрирования).
179.
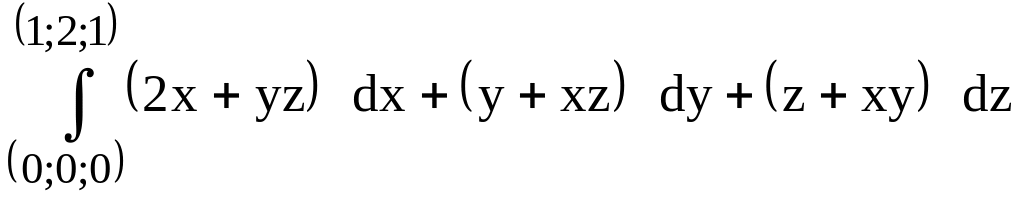 (предварительно убедиться, что он не
зависит от пути интегрирования).
(предварительно убедиться, что он не
зависит от пути интегрирования).
180.
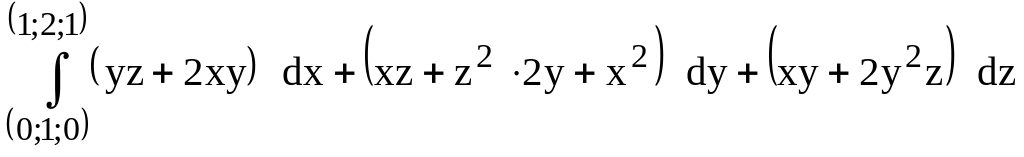 (предварительно убедиться, что он не
зависит от пути интегрирования).
(предварительно убедиться, что он не
зависит от пути интегрирования).
181.
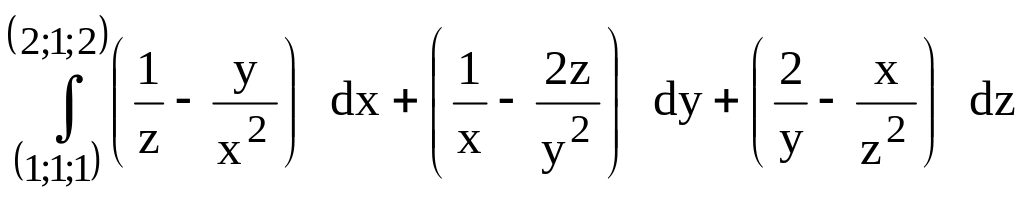 (предварительно
убедиться, что он не зависит от пути
интегрирования).
(предварительно
убедиться, что он не зависит от пути
интегрирования).
182.
![]() правый лепесток лемнискаты
правый лепесток лемнискаты
![]() .
.
183.
![]()
184.
![]() .
.
185.
![]() .
.
186.![]() (в первом квадранте).
(в первом квадранте).
187.![]() .
.
188.
![]() (в первом квадранте).
(в первом квадранте).
189.
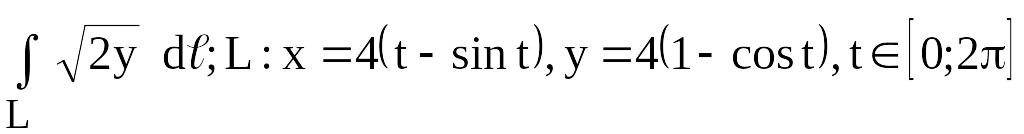 .
.
190.
![]() .
.
191.
![]()
192.
![]()
193.
![]()
194.
![]() дуга кривой у=х2
от А (0;0) до
В (1;3).
дуга кривой у=х2
от А (0;0) до
В (1;3).
195.
![]()
196.
![]() прямая от (0;0) до (1;1).
прямая от (0;0) до (1;1).
197.
![]() при у
0 (по часовой стрелке ).
при у
0 (по часовой стрелке ).
198.
![]() от
(0;1) до (1;
от
(0;1) до (1;
![]() )
.
)
.
199.
![]() (в первом квадранте).
(в первом квадранте).
200.
![]() .
.
201.
![]()
202.
![]()
203.
![]() прямая от (0;0) до (;).
прямая от (0;0) до (;).
204.
![]() прямая от (1;3) до (2;5).
прямая от (1;3) до (2;5).
205.
![]() .
(По формуле Грина – Римана).
.
(По формуле Грина – Римана).
206.
![]() прямая от (1;1;1) до (2;3;4).
прямая от (1;1;1) до (2;3;4).
207.
![]() контур треугольника АВС, где А (0;0), В
(2;0), С (2,2); по формуле Грина – Римана.
контур треугольника АВС, где А (0;0), В
(2;0), С (2,2); по формуле Грина – Римана.
208.
![]() по формуле Грина – Римана.
по формуле Грина – Римана.
209.
![]() прямая от (1;3) до (4;5).
прямая от (1;3) до (4;5).
210.
![]()
211.
![]() от (0;0) до (1;1).
от (0;0) до (1;1).
212.
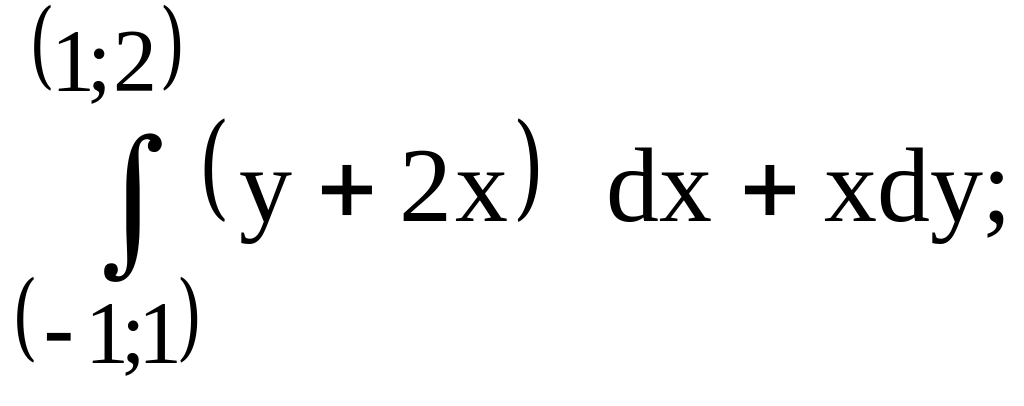 предварительно
убедиться, что он не зависит от
пути интегрирования.
предварительно
убедиться, что он не зависит от
пути интегрирования.
213.
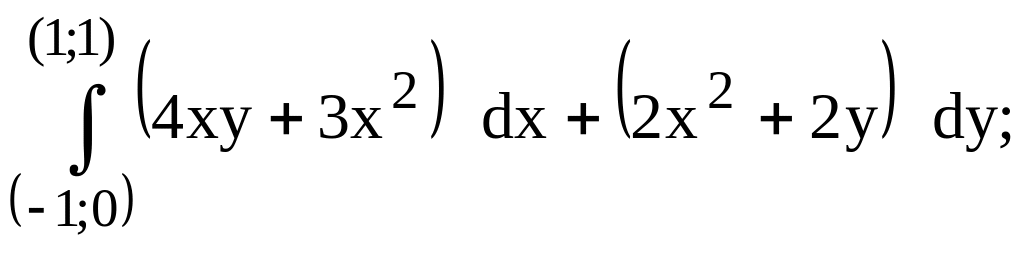 предварительно убедиться, что он
не зависит от пути интегрирования.
предварительно убедиться, что он
не зависит от пути интегрирования.
214.
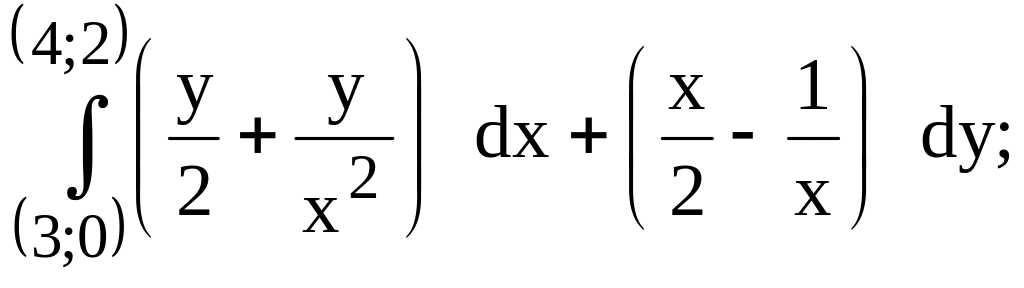 предварительно убедиться, что он не
зависит от пути интегрирования.
предварительно убедиться, что он не
зависит от пути интегрирования.
215.
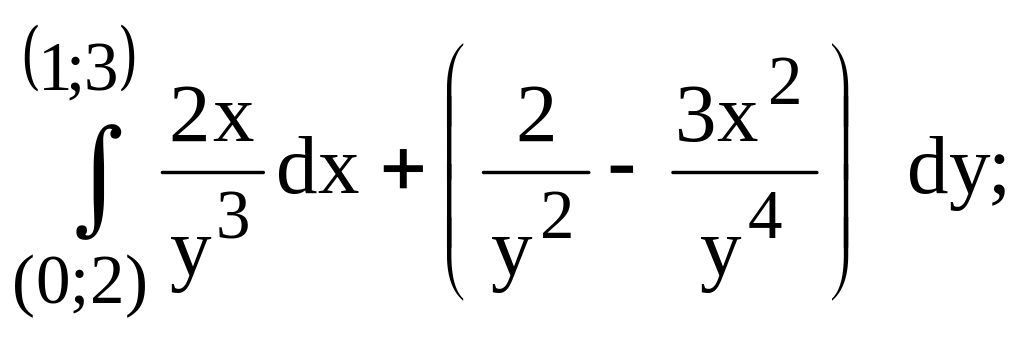 предварительно убедиться, что он не
зависит от пути интегрирования.
предварительно убедиться, что он не
зависит от пути интегрирования.
216.
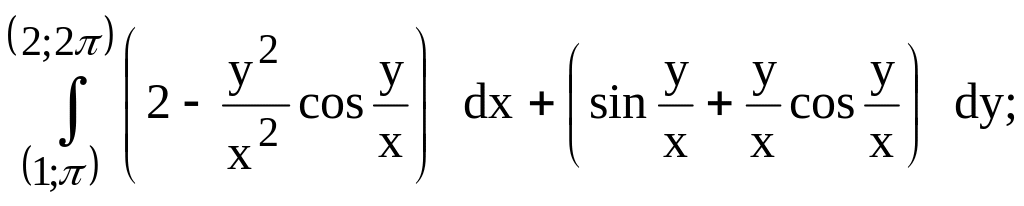 предварительно убедиться,
что он не зависит от пути интегрирования.
предварительно убедиться,
что он не зависит от пути интегрирования.
217.
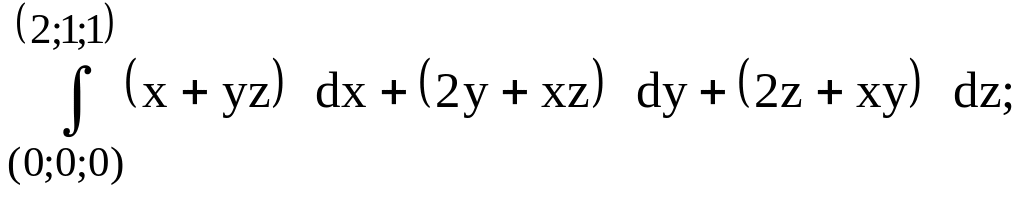 предварительно убедиться,
что он не зависит от пути интегрирования.
предварительно убедиться,
что он не зависит от пути интегрирования.
218.
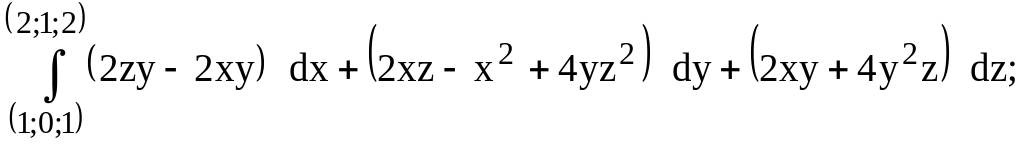 предварительно убедиться, что он не
зависит от пути интегрирования.
предварительно убедиться, что он не
зависит от пути интегрирования.
219.
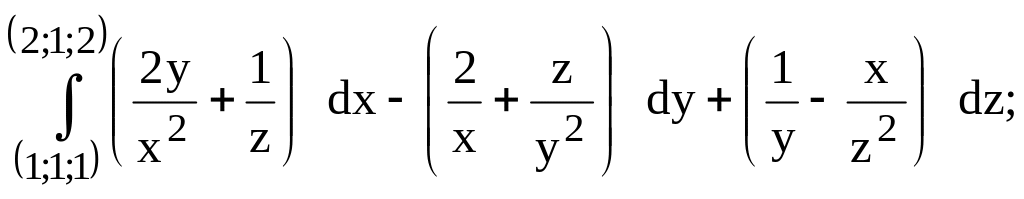 предварительно убедиться, что он не
зависит от пути интегрирования.
предварительно убедиться, что он не
зависит от пути интегрирования.
220.
![]()
221.
![]()
222.
![]() в первом квадранте.
в первом квадранте.
223.
![]() .
.
224.
![]() в первом квадранте.
в первом квадранте.
225.
![]() .
.
226.
![]() .
.
227.
![]() .
.
228.
![]() .
.
229.
![]()
230.
![]() .
.
231.
![]()
232.
![]() прямая от (0;0) до (1;2).
прямая от (0;0) до (1;2).
233.
![]() по часовой стрелке.
по часовой стрелке.
234.
![]() от (0;1) до (1;е).
от (0;1) до (1;е).
235.
![]() в первом квадранте.
в первом квадранте.
236.
![]() .
.
237.
![]()
238.
![]() .
.
239.
![]()
240.
![]() прямая от (0;0) до (;2).
прямая от (0;0) до (;2).
241. прямая от (1;3) до (2;5).
242.
![]() по
формуле Грина – Римана.
по
формуле Грина – Римана.
243.
![]() прямая от (2;2;2) до (2;4;5).
прямая от (2;2;2) до (2;4;5).
244.
![]() по формуле Грина – Римана.
по формуле Грина – Римана.
245.
![]() контур треугольника АВС, где А (0;0), В
(1;0), С (1;1); по формуле Грина – Римана.
контур треугольника АВС, где А (0;0), В
(1;0), С (1;1); по формуле Грина – Римана.
246.
![]() прямая от (1;3) до (4;5).
прямая от (1;3) до (4;5).
247.
![]() по формуле Грина – Римана.
по формуле Грина – Римана.
248.
![]() .
.
249.
 предварительно
убедиться, что он не зависит
от пути интегрирования.
предварительно
убедиться, что он не зависит
от пути интегрирования.
250.
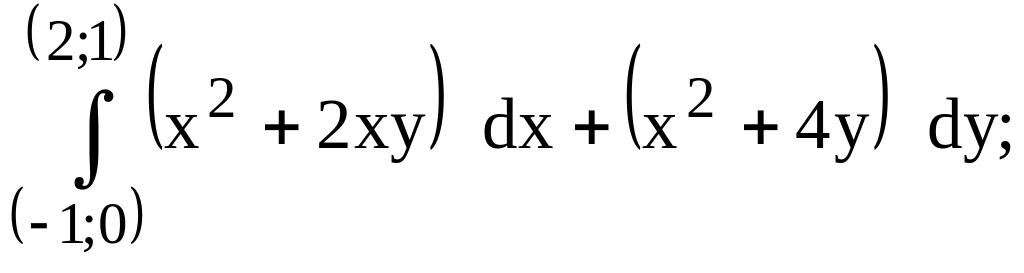 предварительно убедиться, что он не
зависит от пути
интегрирования.
предварительно убедиться, что он не
зависит от пути
интегрирования.
251.
 предварительно убедиться, что он не
предварительно убедиться, что он не
зависит от пути интегрирования.
252.
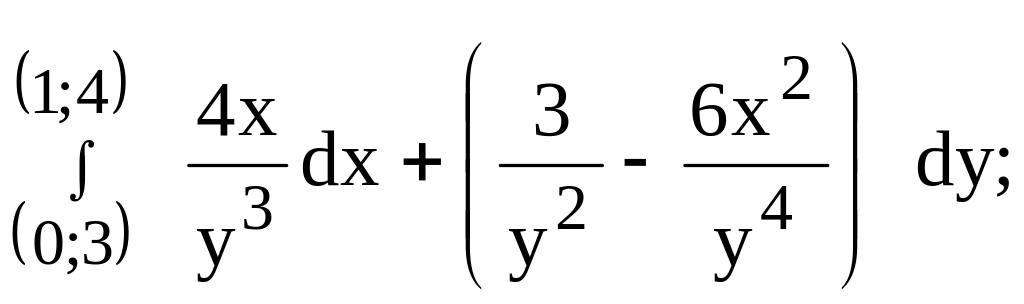 предварительно убедиться, что он не
зависит от пути интегрирования.
предварительно убедиться, что он не
зависит от пути интегрирования.
253.
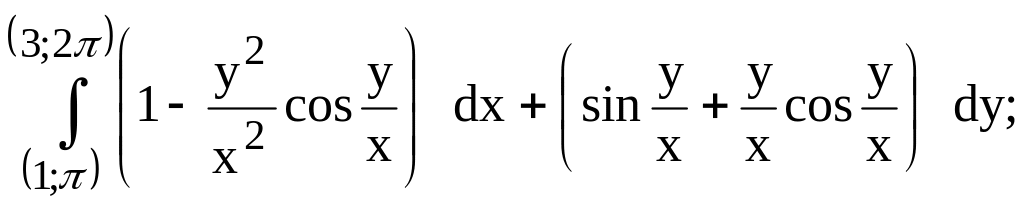 предварительно убедиться, что он не
зависит от пути интегрирования.
предварительно убедиться, что он не
зависит от пути интегрирования.
254.
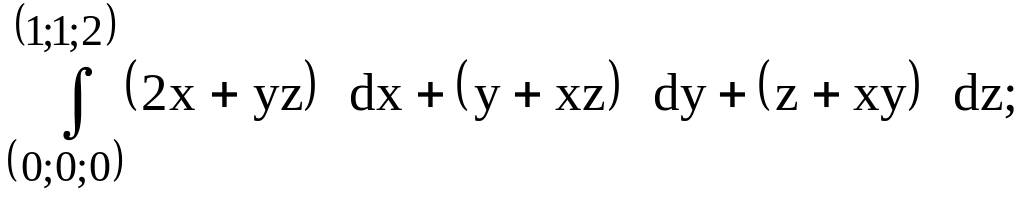 предварительно убедиться, что он не
зависит от пути интегрирования.
предварительно убедиться, что он не
зависит от пути интегрирования.
255.
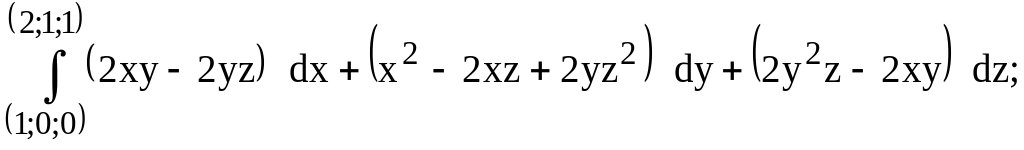 предварительно убедиться, что он не
зависит от пути интегрирования.
предварительно убедиться, что он не
зависит от пути интегрирования.
256.
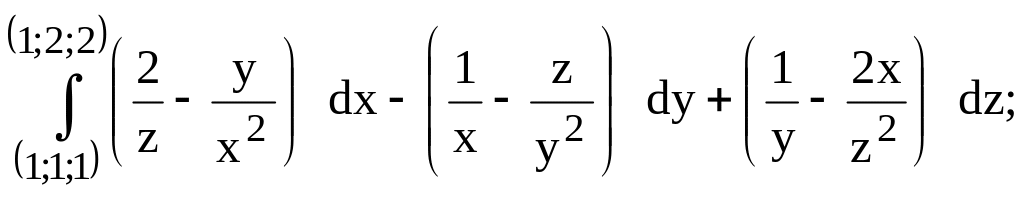 предварительно убедиться, что
он не зависит от пути интегрирования.
предварительно убедиться, что
он не зависит от пути интегрирования.
257.
![]()
258.
![]()
259.
![]() в
первом квадранте.
в
первом квадранте.
260.
![]() .
.
261.
![]() в первом квадранте.
в первом квадранте.
262.
![]() .
.
263.
![]() .
.
264.
![]()
265.
![]() .
.
266.
![]() .
.
267.
![]() от (0;0) до (1;2).
от (0;0) до (1;2).
268.
![]() прямая от (0;0) до (1;3).
прямая от (0;0) до (1;3).
269.
![]() при у
0, по часовой стрелке.
при у
0, по часовой стрелке.
270.
![]() от (0;1) до (1;
от (0;1) до (1;![]() ).
).
271.
![]() в первом квадранте.
в первом квадранте.
272.
![]() .
.
273.
![]()
274.
![]() .
.
275.
![]() прямая от (0;0) до (;).
прямая от (0;0) до (;).
276. прямая от (1;3) до (2;5).
277.
![]() по формуле Грина – Римана.
по формуле Грина – Римана.
278.
![]() прямая от (1;–1;–1) до (2;1;2).
прямая от (1;–1;–1) до (2;1;2).
279.
![]() по формуле Грина – Римана.
по формуле Грина – Римана.
280.
![]() контур треугольника АВС, где А (0;0), В
(2;0), С (2;2); по формуле Грина – Римана.
контур треугольника АВС, где А (0;0), В
(2;0), С (2;2); по формуле Грина – Римана.
281.
![]() прямая от (1;3) до (4;5).
прямая от (1;3) до (4;5).
282.
![]()
283.
![]() от (1;1) до (2;2).
от (1;1) до (2;2).
284.
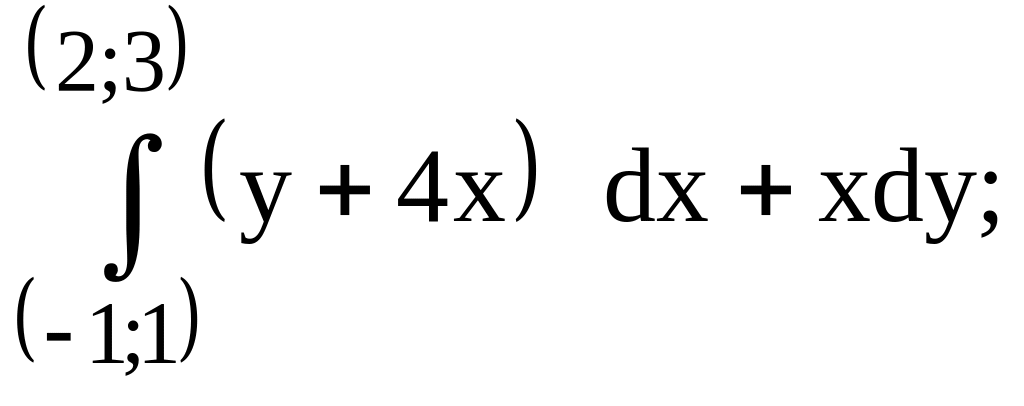 предварительно убедиться, что он не
зависит от пути интегрирования.
предварительно убедиться, что он не
зависит от пути интегрирования.
285.
![]() прямая от (1;1;1) до (3;2;4).
прямая от (1;1;1) до (3;2;4).
286.
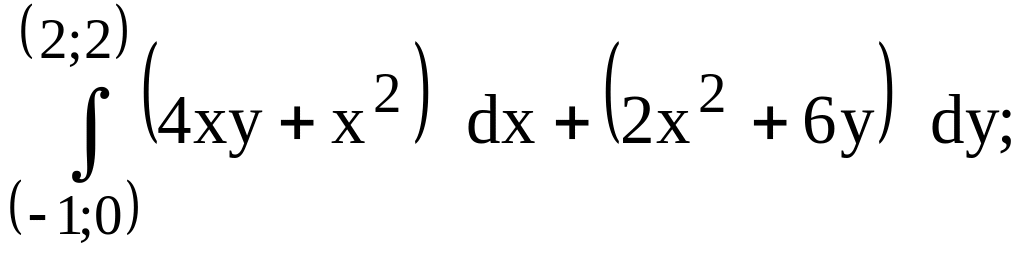 предварительно убедиться, что он не
зависит от пути интегрирования.
предварительно убедиться, что он не
зависит от пути интегрирования.
287.
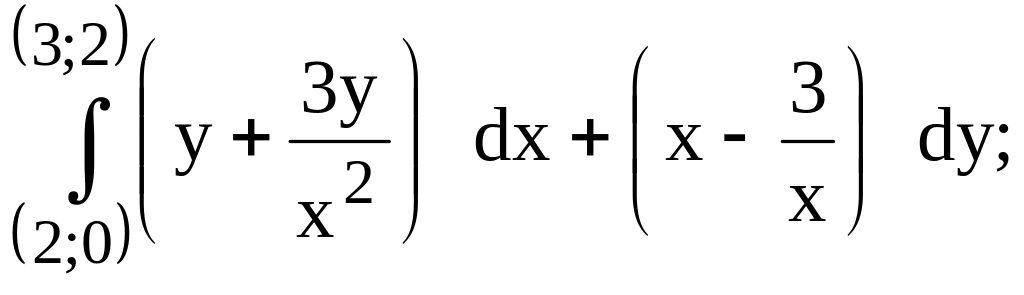 предварительно убедиться, что он не
зависит от пути интегрирования.
предварительно убедиться, что он не
зависит от пути интегрирования.
288.
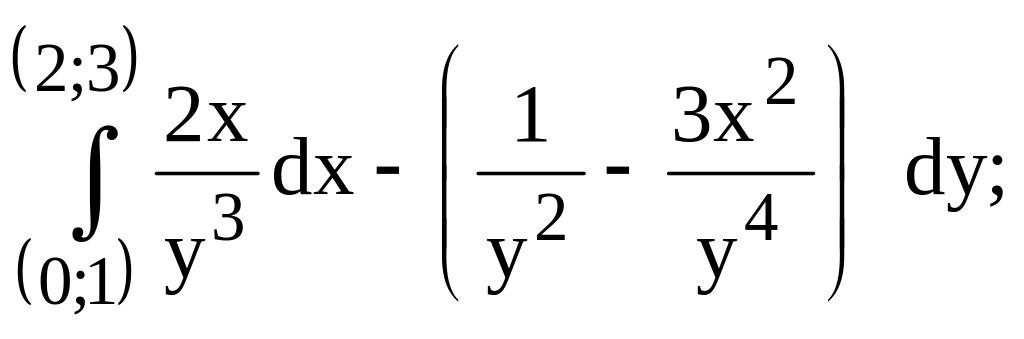 предварительно убедиться, что он не
зависит от пути интегрирования.
предварительно убедиться, что он не
зависит от пути интегрирования.
289.
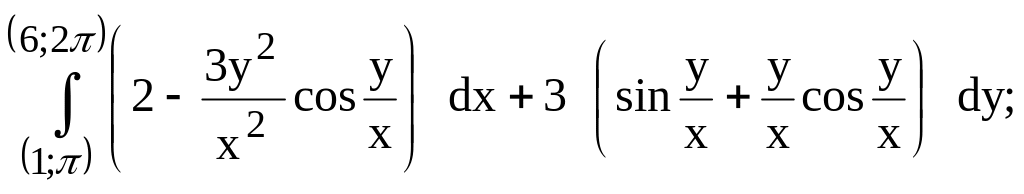 предварительно убедиться, что он не
зависит от пути интегрирования.
предварительно убедиться, что он не
зависит от пути интегрирования.
290.
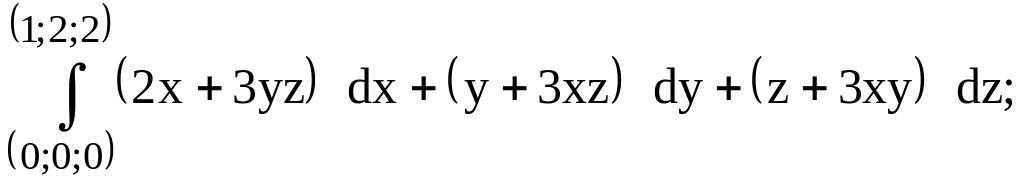 предварительно убедиться, что он не
зависит от пути интегрирования.
предварительно убедиться, что он не
зависит от пути интегрирования.
291.
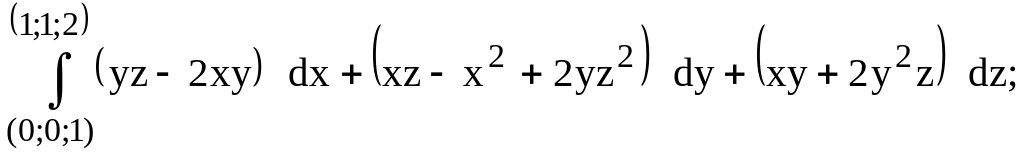 предварительно убедиться, что он не
зависит от пути интегрирования.
предварительно убедиться, что он не
зависит от пути интегрирования.
292.
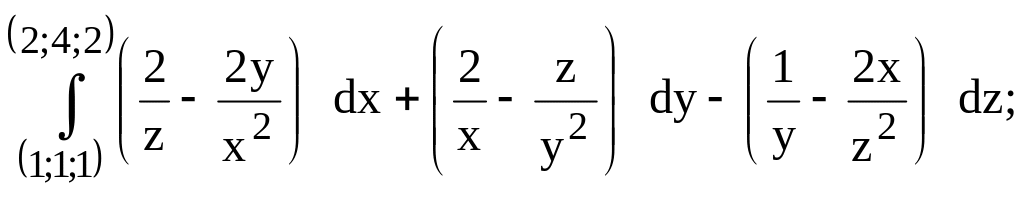 предварительно убедиться, что он не
зависит от пути интегрирования.
предварительно убедиться, что он не
зависит от пути интегрирования.
293.
![]() в первом квадранте.
в первом квадранте.
294.
![]() .
.
295.
![]() .
.
296.
![]() прямая от (0;0) до (1;2).
прямая от (0;0) до (1;2).
297.
![]() при у
0, по часовой стрелке.
при у
0, по часовой стрелке.
298.
![]() от (0;1) до (1;е).
от (0;1) до (1;е).
299.
![]() в первом квадранте.
в первом квадранте.
300.
![]() .
.
301.
![]() прямая от (0;0) до (;2).
прямая от (0;0) до (;2).
302.
![]() прямая от (1;–1;–1) до (2;1;2).
прямая от (1;–1;–1) до (2;1;2).
303.
![]() по формуле Грина – Римана.
по формуле Грина – Римана.
304.
![]() контур треугольника АВС, где А(0;0), В(1;0),
С (1;1); по формуле Грина – Римана.
контур треугольника АВС, где А(0;0), В(1;0),
С (1;1); по формуле Грина – Римана.
305. прямая от (1;3) до (4;5).
306.
![]() по формуле Грина.
по формуле Грина.
307.
![]() прямая от (1;1;1) до (3;2;4).
прямая от (1;1;1) до (3;2;4).
308.
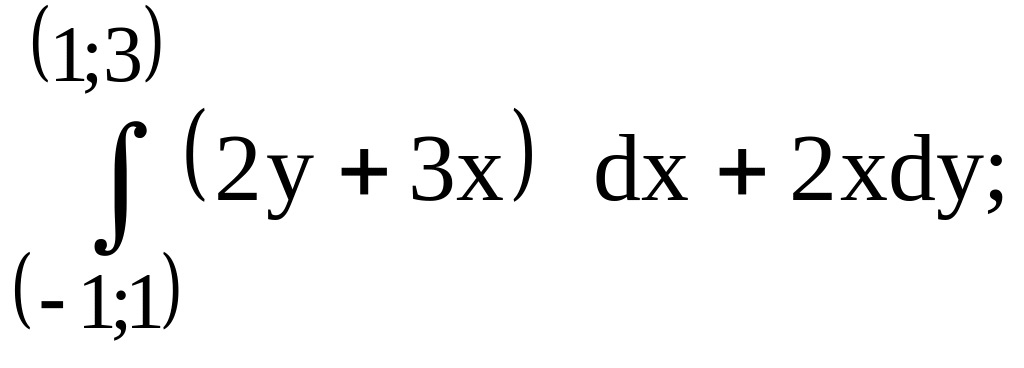 предварительно
убедиться, что он не зависит от пути
интегрирования.
предварительно
убедиться, что он не зависит от пути
интегрирования.
309.
![]() прямая от (1;1;1) до (3;2;4).
прямая от (1;1;1) до (3;2;4).
310.
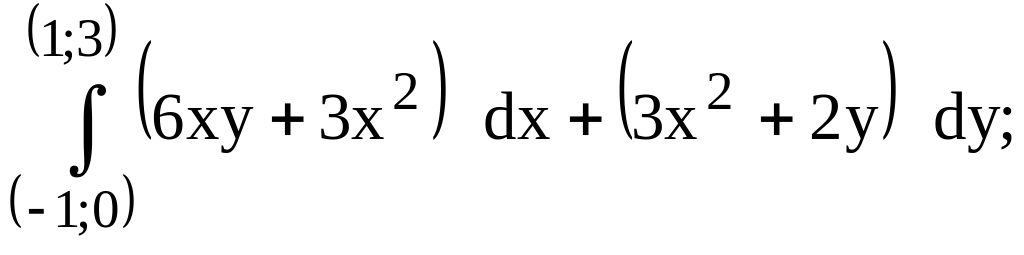 предварительно
убедиться, что он не зависит от пути
интегрирования.
предварительно
убедиться, что он не зависит от пути
интегрирования.
311.
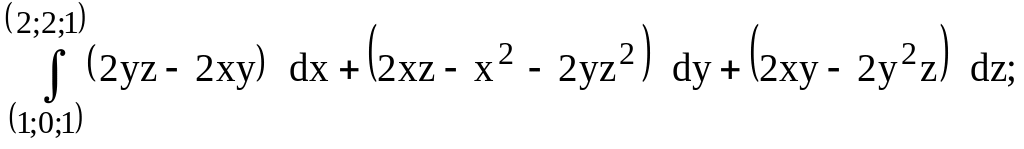 предварительно убедиться, что он не
зависит от пути интегрирования.
предварительно убедиться, что он не
зависит от пути интегрирования.
312.
 предварительно убедиться, что он не
зависит от пути интегрирования.
предварительно убедиться, что он не
зависит от пути интегрирования.
313.
![]()
314. Вычислить
площадь части поверхности параболоида
![]() вырезанной цилиндром
вырезанной цилиндром
![]()
315.
![]() отсеченная плоскостью z=1.
отсеченная плоскостью z=1.
316.
![]()
