
- •Случайные события Некоторые сведения из теории множеств
- •Основные формулы комбинаторики
- •Случайные события, их виды
- •Вероятность событий
- •Теоремы умножения и сложения вероятностей Условная вероятность
- •Вероятностные модели с усреднением вероятности
- •Случайные величины
- •Дискретные случайные величины
- •Числовые характеристики дискретных случайных величин
- •Непрерывные случайные величины Функция и плотность распределения непрерывной случайной величины
- •Числовые характеристики непрерывных случайных величин
- •Основные распределения непрерывных случайных величин
- •Математическая статистика
- •Выборочный метод
- •Статистические оценки параметров распределения
Основные распределения непрерывных случайных величин
Равномерное. Распределение вероятностей называется равномерным, если на интервале возможных значений случайной величины плотность распределения является постоянной.
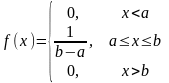
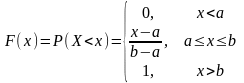
Пример 1. Н.с.в. X-размер авторского вознаграждения, выплачиваемого издательством писателю имеет равномерное распределение в интервале от 1 до 10 тыс. рублей. Найти вероятность того, что писатель получит от издательства более 6 тыс. рублей, найти средний размер вознаграждения и СКО н.с.в. X.
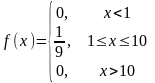
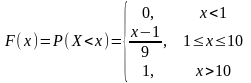
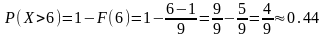

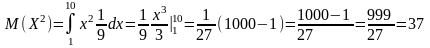
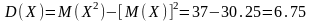
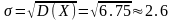
Нормальное
распределение (распределение Гаусса).
Общим нормальным распределением
вероятностей н.с.в. X называется
распределение с плотностью
![]() .
.
Нормальное распределение задается двумя параметрами: a и s - его математическим ожиданием и СКО.
Нормальное распределение с параметрами a=0 и s=1 называется нормированным (или стандартным); его плотность
Математическая статистика
Цель математической статистики состоит в создании методов сбора и группировки статистических данных для получения научных и практических выводов.
Первая задача математической статистики состоит в указании методов сбора и группировки статистических сведений, которые получены в результате экспериментов или наблюдений. Вторая задача – это разработка методов анализа статистических данных: оценки неизвестных вероятности события, а также функций и параметров распределения; оценка зависимости случайной величины от других случайных величин; проверка статистических гипотез о виде и величинах параметров неизвестного распределения.
Выборочный метод
Определение.
Все значения, которые может принимать
случайная величина X , образуют генеральную
совокупность X.
При выполнении экспериментов (испытаний)
из генеральной совокупности извлекаются
значения
 ,
которые называются выборочными
значениями,
а массив выборочных значений называется
выборочной
совокупностью или выборкой.
Количество выборочных значений n - объем
выборки.
,
которые называются выборочными
значениями,
а массив выборочных значений называется
выборочной
совокупностью или выборкой.
Количество выборочных значений n - объем
выборки.
Пример 1. Пусть из 2000 изделий отобрано для исследования 100 изделий. Тогда объем генеральной совокупности N=2000, а объем выборки n=100.
Выборку можно осуществлять двумя способами. Если после исследования объект возвращается в генеральную совокупность, то такая выборка называется повторной (возвратной); если объект не возвращается в генеральную совокупность, то выборка называется бесповторной (безвозвратной).
Определение. Выборка называется репрезентативной (представительной), если по ее данным можно достаточно уверенно судить об интересующем нас признаке генеральной совокупности.
Определение.
Пусть из генеральной совокупности
извлечена выборка объема n,
в
которой значение
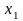 некоторого
исследуемого признака X
наблюдалось
некоторого
исследуемого признака X
наблюдалось
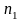 раз,
значение
раз,
значение
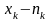 раз. Значения
раз. Значения
 называются вариантами,
а их последовательность, записанная в
возрастающем порядке, - вариационным
рядом.
Числа
называются вариантами,
а их последовательность, записанная в
возрастающем порядке, - вариационным
рядом.
Числа
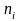 называются частотами,
а их отношения к объему выборки
называются частотами,
а их отношения к объему выборки
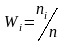 -
относительными
частотами.
При этом
-
относительными
частотами.
При этом
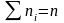 ,
а
,
а
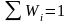 .
.
Определение. Модой M0 называется варианта, имеющая наибольшую частоту.
Определение.
Медианой
Mе
называется
варианта, которая делит пополам
вариационный ряд на две части с одинаковым
числом вариант в каждой. Если число
вариант нечетное, то есть
 ,
то
,
то
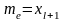 ;
если же число вариант четно, то есть
;
если же число вариант четно, то есть
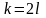 ,
то
,
то
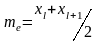 .
.
Определение.
Размахом
варьирования
называется разность между максимальной
и минимальной вариантами или длина
интервала, которому принадлежат все
варианты выборки:
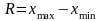 .
.
Определение. Перечень вариант и соответствующих им частот называется статистическим распределением выборки.
Пример 2. Выборка задана в виде распределения частот:
xi |
4 |
7 |
8 |
12 |
17 |
ni |
2 |
4 |
5 |
6 |
3 |
Найти распределение относительных частот и основные характеристики вариационного ряда.
Найдем
объем выборки: n=2+4+5+6+3=20. Относительные
частоты равны:
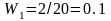 ;
;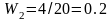 ;
;
 ;
;
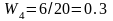 ;
;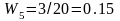 .
Контроль: 0.1+0.2+0.25+0.3+0.15=1. Распределение
относительных частот имеет вид:
.
Контроль: 0.1+0.2+0.25+0.3+0.15=1. Распределение
относительных частот имеет вид:
xi |
4 |
7 |
8 |
12 |
17 |
Wi |
0.1 |
0.2 |
0.25 |
0.3 |
0.15 |
Мода этого
вариационного ряда равна 12. Число вариант
нечетно,
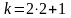 ,
поэтому медиана равна
,
поэтому медиана равна
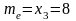 .
Размах варьирования
.
Размах варьирования
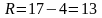 .
.
Определение. Функция, определяющая для каждого значения x относительную частоту события X<x,
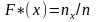 называется
эмпирической
функцией распределения,
или функцией
распределения выборки.
называется
эмпирической
функцией распределения,
или функцией
распределения выборки.
В
отличие от эмпирической функции
распределения
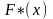 выборки функция распределения
генеральной
совокупности называется теоретической
функцией распределения.
Эмпирическая функция распределения
обладает следующими свойствами:
выборки функция распределения
генеральной
совокупности называется теоретической
функцией распределения.
Эмпирическая функция распределения
обладает следующими свойствами:
значения принадлежат отрезку [0;1];
является неубывающей функцией;
пусть
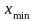 и
и
 -
соответственно, минимальная и максимальная
варианты, тогда
-
соответственно, минимальная и максимальная
варианты, тогда
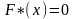 при
при
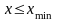 и
и
 при
при
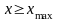 .
.
Эмпирическая функция распределения служит для оценки теоретической функции распределения генеральной совокупности.
Пример 3. Построить эмпирическую функцию распределения по заданному распределению выборки:
xi |
2 |
4 |
6 |
ni |
10 |
15 |
25 |
Объем выборки n=10+15+25=50.
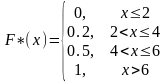
Каждую
пару значений
 из распределения выборки можно трактовать
как точку на координатной плоскости.
Точно также можно рассматривать и пары
значений
из распределения выборки можно трактовать
как точку на координатной плоскости.
Точно также можно рассматривать и пары
значений
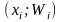 относительного распределения выборки.
Ломаная, отрезки которой соединяют
точки
,
называется полигоном
частот.
Ломаная, соединяющая точки
,
называется полигоном
относительных частот.
относительного распределения выборки.
Ломаная, отрезки которой соединяют
точки
,
называется полигоном
частот.
Ломаная, соединяющая точки
,
называется полигоном
относительных частот.
Для
случая непрерывного признака X удобнее
разбить
интервал
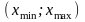 его наблюдаемых значений на несколько
частичных интервалов длиной h каждый и
найти для каждого из этих интервалов
сумму частот
его наблюдаемых значений на несколько
частичных интервалов длиной h каждый и
найти для каждого из этих интервалов
сумму частот
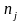 ,
попавшихв него.
,
попавшихв него.
Ступенчатая
фигура,
состоящая из прямоугольников с основаниями
длиной h
и
высотами
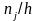 (плотность
частоты), называется гистограммой
частот.
Геометрический смысл гистограммы: ее
площадь равна объему выборки.
(плотность
частоты), называется гистограммой
частот.
Геометрический смысл гистограммы: ее
площадь равна объему выборки.
Ступенчатая
фигура,
состоящая из прямоугольников с основаниями
длиной h
и
высотами
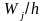 ,
называется гистограммой
относительных частот.
Геометрический смысл гистограммы
относительных частот: ее площадь равна
1.
,
называется гистограммой
относительных частот.
Геометрический смысл гистограммы
относительных частот: ее площадь равна
1.
