Множество. Основные понятия (Определение, принадлежность элемента множеств, подмножество множества, включение множества, равенство множеств, собственное подмножество, мощность множества, пустое множество, универсальное множество).
Множество – совокупность определенных различаемых объектов, для которых можно установить принадлежит данный объект множеству или нет.
Объекты, из которых состоит множество, называют элементами множества или точками множества. Множества чаще всего обозначают заглавными буквами латинского алфавита, его элементы — строчными. Если а — элемент множества А, то записывают а ∈ А (а принадлежит А). Если а не является элементом множества А, то записывают а ∉ А (а не принадлежит А).
А называется подмножеством множества В, если всякий элемент А является элементом В.
Если каждый элемент множества A входит в B, но множество B содержит хотя бы один элемент, не входящий в A, то A называется собственным подмножеством B, а B - собственным надмножеством A.
Число элементов конечного множества М называется его мощностью |М|.
Множество мощности 0 называется пустым. Пустое множество является подмножеством любого множества.
Универсальное множество — это такое множество, которое состоит из всех элементов, а так же подмножеств множества объектов исследуемой области. Универсальное множество может выбираться самостоятельно, в зависимости от рассматриваемого множества, и решаемых задач.
Множество. Способы задания множеств (перечислением или списком, порождающей процедурой, описанием характеристического свойства). Привести примеры.
Множество – совокупность определенных различаемых объектов, для которых можно установить принадлежит данный объект множеству или нет.
перечисление всех его элементов;
порождающей процедурой;
описание характеристического (общего) свойства его элементов.
Первым способом задаются конечные множества.
Примеры:
А – множество чисел, являющихся делителями числа 20: А = {1, 2, 4, 5, 10, 20}.
В – список группы: В = {Архипов, Белов,…}.
Задание множеств
порождающей процедурой или арифметическими
операциями означает описание
характеристических свойств элементов
множества:
,
т. е. множество Х содержит такие элементы
Х , которые обладают свойством Н(х) .
Например:
,
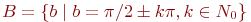N0
- множество
всех натуральных чисел;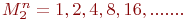
или
;
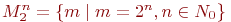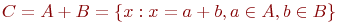
Третьим способом можно задать конечные множества, бесконечные, пустые. Множество элементов. Обладающих характеристическим свойством Р, обозначается:
{x | P(x)} и читается так: множество всех х таких, что х обладает свойством Р(х).
Примеры:
{x | x R, x2 – 4 = 0} - это конечное множество и его можно задать перечислением элементов : {2, -2}.
{x | x R, 2< x < 5 } – бесконечное несчетное множество, а именно, числовой промежуток (2, 5).
{x | x R, 1= sinx} – бесконечное счетное множество.
{x | x R, x2 + 9 = 0 } – это пустое множество, т.к. ни одно вещественное число не удовлетворяет данному уравнению.
Операции над множествами (объединение, пересечение, разность, симметрическая разность, дополнение). Диаграммы Венна. Изобразить с помощью диаграмм Эйлера-Венна операции над множествами. Привести примеры.
Объединением
множеств называется множество, состоящее
из всех тех элементов, которые принадлежат
хотя бы одному из множеств А или В.
Пересечением
множеств называется множество, состоящее
из элементов, входящих как в множество
А , так и в множество В.
Разностью множеств
называется множество всех элементов
множества А , которые не содержатся в
В.
Симметричная
разность множеств А и В,
:
Дополнением (до
универсального множества ) множества
называется множество всех элементов,
не принадлежащих , но принадлежащих
универсальному множеству.
Алгебра множеств. Законы алгебры множеств. Доказать один из законов алгебры множеств.
Для операций объединения, пересечения и дополнения выполняются следующие законы:
коммутативности:
ассоциативности:
дистрибутивности:
пересечения
относительно объединения:
объединение
относительно пересечения:
идемпотентности:
действия с
универсальным и пустым множествами:
де Моргана:
двойного дополнения:
Поглощение:
Доказательства. Некоторые приемы доказательств (графический; доказательство равенства соотношений типа X=Y; от противного). Примеры доказательства равенства множеств.
Приемы доказательств в теории множеств:
Графический метод.
Доказательство равенств.
Доказательство от противного.
Для графического метода используется диаграммы Эйлер-Венна. Для этого строится диаграмма левого и правого части равенств.
Согласно доказательству равенст:
а∈Х => а∈Y, если b∈X то b∉Y
X=Y если X Y, Y X;
Пример:
Если
и
и
или
или
Необходимо
доказать включение в обратную сторону:
или
или
и
и
.
Следовательно
Q – утверждение; P – исходящее утверждение;
Предполагается, что Q – ложно, в таком случае имеет место противоречию следовательно предположение ложно, то есть Q – истинно.