Разложение произвольного вектора по ортам координатных осей на плоскости и в пространстве.

В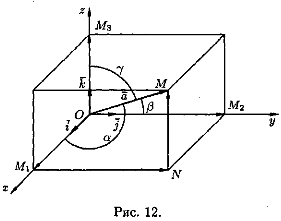 ПРОСТРАНСТВЕ. Рассмотрим в пространстве прямоугольную систему координат Oxyz. Выделим на координатных осях Ох, Оу и Oz единичные векторы (орты), обозначаемые i , j , k соответственно.

Выберем произвольный вектор а пространства и совместим его начало с началом координат: а=ОМ. Найдем проекции вектора а на координатные оси. Проведем через конец вектора ОМ плоскости, параллельные координатным плоскостям. Точки пересечения этих плоскостей с осями обозначим соответственно через М₁ , М₂ и Мз. Получим прямоугольный параллелепипед, одной из диагоналей которого является вектор ОМ. Тогда пр _ха=|OM ₁|, np_ya = |ОМ₂|, пр_z а=|ОМз|. По определению суммы нескольких векторов находим а = ОМ ₁ + M₁N + NM. А так как M₁N=OM₂ , NM =ОМз, то а=ОМ₁ + ОМ₂ + ОМ₃

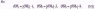
Обозначим проекции вектора а=ОМ на оси Ох, Оу и Oz соответственно через а_х, а_у и a_z, т.е. |OM ₁| = а_х,|ОМ₂| = а_у, |ОМ₃| = а_z. Тогда из равенств получаем a=a_xi+a_yj+a_zk

Эта формула является основной в векторном исчислении и называется разложением вектора по ортам координатных осей. Числа а_х, а_у, a_z называются координатами вектора а, т. е. координаты вектора есть его проекции на соответствующие координатные оси.

НА ПЛОСКОСТИ

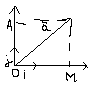Вектор а =ОМ+ОА. Т.к. ОМ коллинеарен i , а ОА коллинеарен j, то вектор а=ОМ×i + OA×j

Действия с векторами в координатной форме

Как и координата вектора на прямой, координаты вектора на плоскости обладают следующими свойствами:

С в о й с т в о 1. При сложении векторов их соответствующие координаты складываются.

Пусть a=(a_x ; a_y) b=(b_x ; b_y) сумма векторов записывается с=a+b → c=(a_x + b_x ; a_y + b_y) →

C_x=a_x + b_x и c_y=a_y + b_y .

Действительно! С=a+b= (a_x + b_x)×i + (a_y + b_y)×j

С в о й с т в о 2. При умножении вектора на число его координаты умножаются на это число

Пусть а=(а_x ; a_y) и b=αa.

Покажем,что b=(αa_x ; αa_y)

То есть b_x=αa_x и b=αa_y

Действительно ! выполняется равенство b=αa_x×i + αa_y× j

Признак коллинеарности векторов

Коллинеарные векторы – векторы а и b называются таковыми, если они лежат на одной прямой или на параллельных прямых, записываются как a | | b. Коллинеарные векторы могут быть направленны одинаково или противоположно

Выясним условия коллинеарности векторо a и b, заданных своими координатами.

Так как a | | b, то можно записать a =λ × b, где λ-некоторое число.

То есть a_x×i + a_y×j + a_z×k = λ(b_x×i + b_y ×j + b_z×k)=

=λb_x×i + λb_y× j + λb_z×k

Отсюда следует a_x=λb_x a_y=λb_y a_z=λb_z

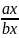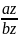То есть =λ ; =λ ; =λ ИЛИ = =

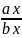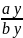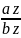
Таким образом, проекции коллинеарных векторов пропорциональны. Верно и обратное утверждение: векторы, имеющие пропорциональные координаты,коллинеарны.

Скалярное произведение векторов и его свойства

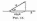Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на косинус угла между ними. a×b=|a|×|b|×cosφ. Если хотя бы один из векторов равен 0,то скалярное произведение равно 0.

Свойства:

1)переместительное(коммунитативность): a · b = b · a

a·b=|a|·|b|·cosφ и также b·a= |b|·|a|·cosφ

2)распределительное: a · (b + c) = a · b + a · c

3)Сочетательное (линейность) относительно скалярного множителя: k · (a · b) = (k · a) · b = a · (k · b) .

4)Скалярный квадрат вектора равен квадрату его модуля: a · a = |a|² (норма вектора)

a²=a·a=|a|·|a|·cos0=|a|·|a|=|a|²

5)если вектора a и b взаимно перпендикулярны,то есть ортогональны,то их скалярное произведение равно нулю,так как cos90°=0

Выражение скалярного произведения ч/з координаты

Пусть заданы два вектора

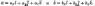
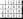Найдем скалярное произведение векторов, перемножая их как многочлены, пользуясь таблицей скалярного произведения векторов i, j, k .

То есть

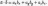
Итак, скалярное произведение векторов равно сумме произведений их одноименных координат.

Уравнение пучка прямых

Пучком прямых на плоскости называется множество всех прямых данной плоскости, имеющих одну общую точку, которая называется центром пучка. пучком прямых называют множество всех прямых, проходящих через заданную точку. Так как все прямые проходят через одну и ту же точку с координатами М₀ (x₀;y₀),то координаты этой точки удовлетворяет уравнениями этих прямых,то есть y₀=kx+b. Вычитая это равенство из y=kx+b,получим y-y₀=k(x-x₀) –это уравнение пучка прямых. Уравнением пучка прямых можно описать любую прямую пучка кроме прямой, перпендикулярной оси Ox,так как в этом случае угловой коэффициент такой прямой не определен. Несобственным пучком прямых называется совокупность прямых, параллельных фиксированной прямой (центром несобственного пучка прямых считается бесконечно удаленная точка плоскости).