MOR_variant_8_inzhekon_18_04_15

1. Дана задача линейного программирования

f=с₁ x₁+с₂ x₂ max (min)

при ограничениях

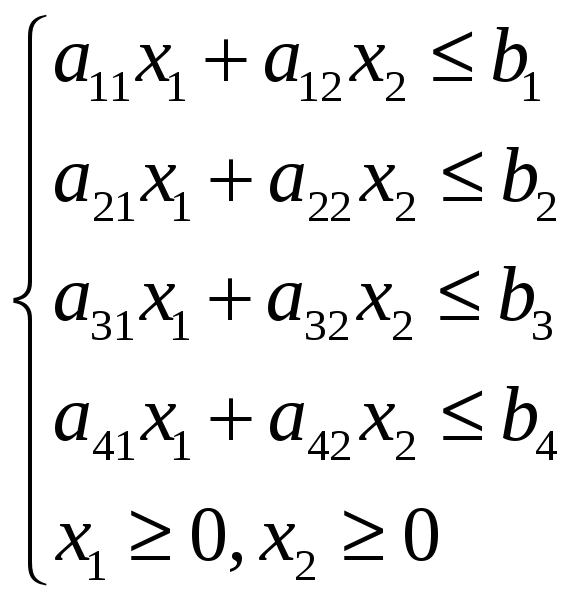
Графическим методом найти оптимальные решения при стремлении целевой функции к максимальному и минимальному значениям.

Решение:

Построим прямые по двум точкам

1) (0,1) (2,0)

2) (0,4) (-6,0)

3) (0,0) (3,2)

2)

Построив прямые, заштрихуем полуплоскости соответствующие данным неравенствам. Получим множество допустимых планов.

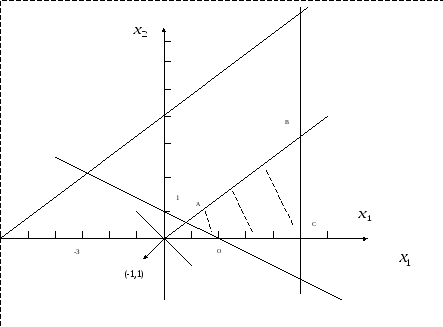
В данном случае областью допустимых решений является треугольник

OAВС.

Далее строим вектор целевой функции – вектор (-1,1).

Перпендикулярно к вектору строим график целевой функции

Передвигая график против вектора , находим точку входа в область допустимых решений – точка А.

Ее координаты

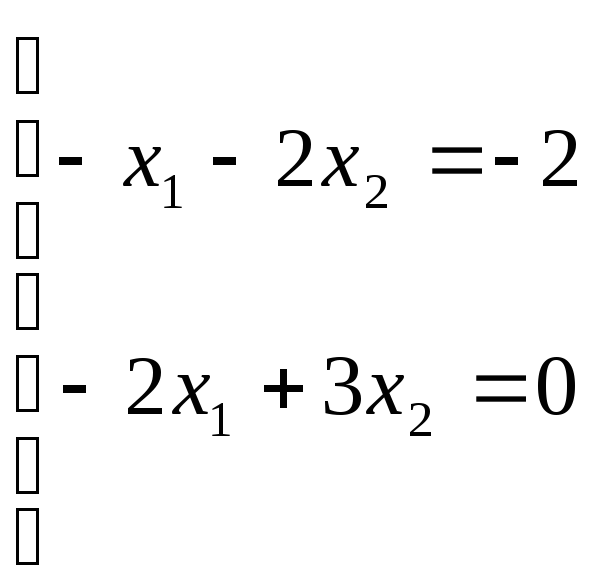
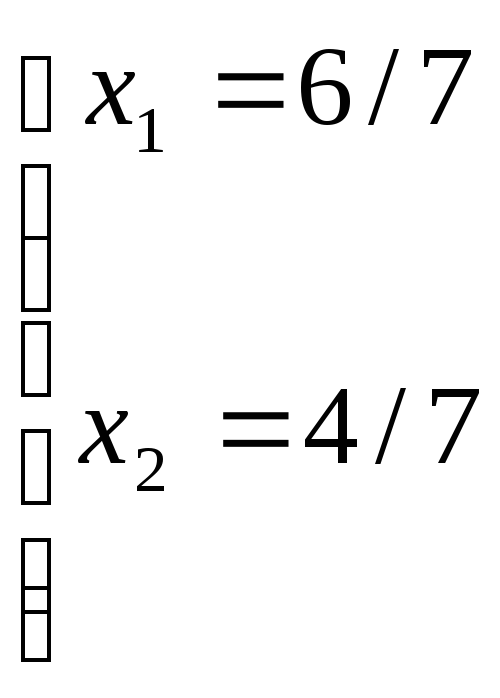
Передвигая график против вектора , находим точку выхода из области допустимых решений – точка В.

Ее координаты

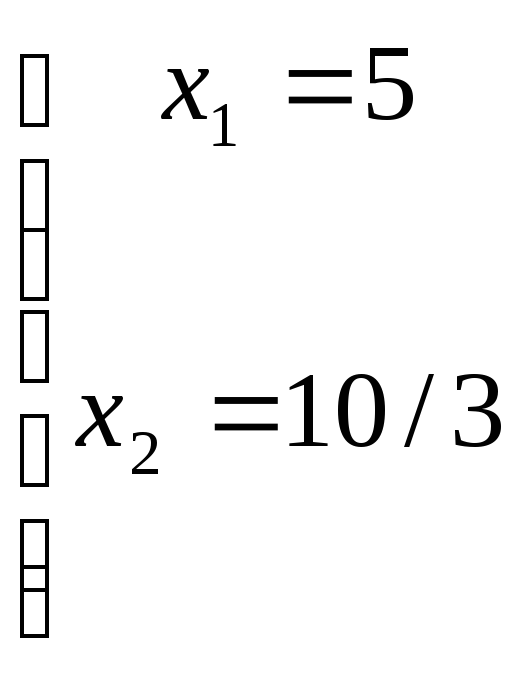
2. Фирма изготовляет два вида красок для внутренних (В) и наружных (Н) работ. Для их производства используют исходные продукты: пигмент и олифу. Расходы исходных продуктов и максимальные суточные запасы указаны в таблице.

Расходы и суточные запасы исходных продуктов

Исходный продукт	Расход исходных продуктов на 1 т краски		Суточный запас, т
	Краска Н	Краска В
Пигмент	1	1	6
Олифа	2	1	8

Изучение рынка сбыта показало, что суточный спрос на краску для внутренних работ никогда не превышает 4,5 т в сутки. Цена продажи 1 т краски для наружных работ ден. ед. Цена продажи 1 т краски для внутренних работ ден. ед.

Какое количество краски каждого вида должна производить фирма, чтобы доход от реализации продукции был максимален?

Решение:

Пусть т. краски Н необходимо изготовить

Пусть т. краски В необходимо изготовить

Составим математическую модель задачи:

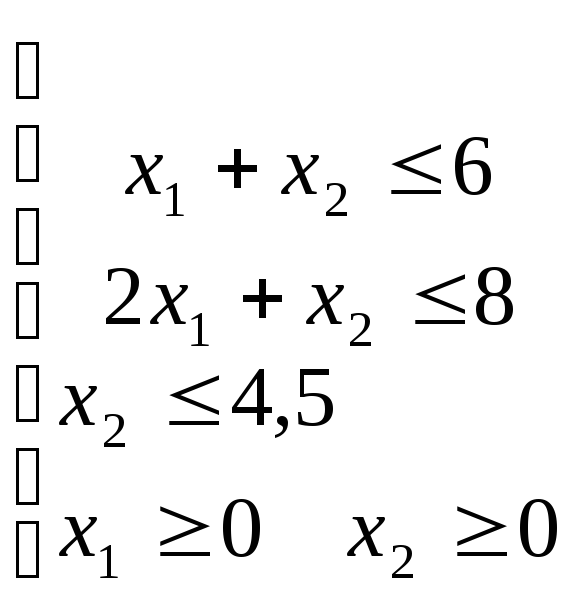
Целевая функция:

Построим прямые по двум точкам

1) (0,6) (6,0)

2) (0,8) (4,0)

3)

Построив прямые, заштрихуем полуплоскости соответствующие данным неравенствам. Получим множество допустимых планов.

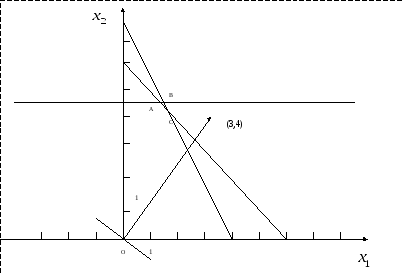
В данном случае областью допустимых решений является треугольник

АВС.

Далее строим вектор целевой функции – вектор (3,4)

Перпендикулярно к вектору строим график целевой функции

Передвигая график вдоль вектора , находим точку выхода из области допустимых решений – точка В.

Ее координаты

Необходимо изготовить 1,75краски Н и 4,5 краски В.

ден.ед.

3. Составить математическую модель и решить задачу симплексным методом.

В производстве пользующихся спросом двух изделий, А или В, принимают участие 3 цеха. На изготовление одного изделия А первый цех затрачивает 7 час, второй цех - 7 час, третий цех - 8 час. На изготовление одного изделия В первый цех затрачивает 13 час, второй цех -8 час, третий цех - 2 час. На производство обоих изделий первый цех может затратить не более 363 час, второй цех не более 327 час, третий цех – не более 429 час.

От реализации одного изделия А фирма получает доход 6 руб., изделие В - 4 руб.

Определить максимальный доход от реализации всех изделий А и В.

Решение:

Пусть изд. А необходимо изготовить

Пусть изд. В необходимо изготовить

Тогда:

- ч. затраты цеха 1;

- ч. затраты цеха 2;

- ч. затраты цеха 3.

- прибыль

Составим математическую модель задачи:

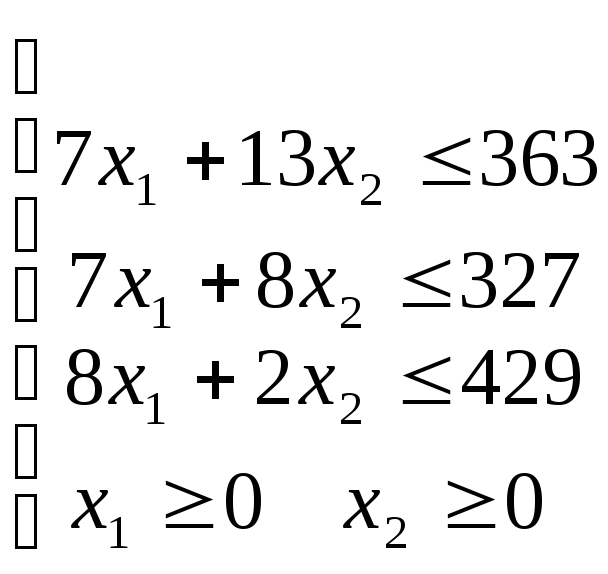
Целевая функция:

Приведем задачу к каноническому виду:

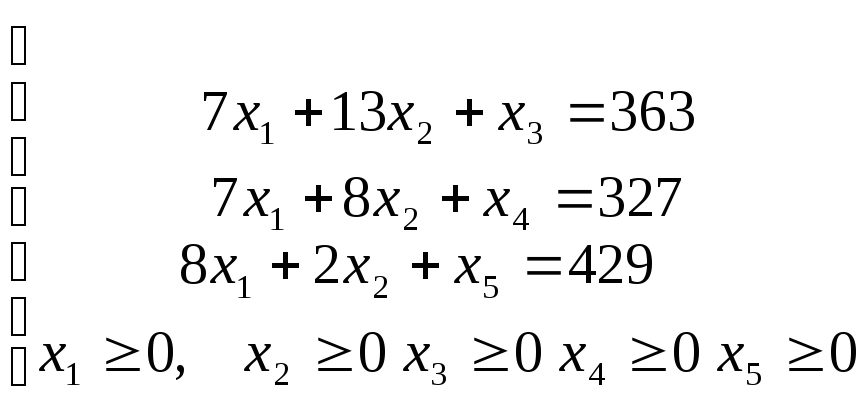
Составим симплекс таблицу:

			6	4	0	0	0
0		363	7	13	1	0	0	363/7=51,9
0		327	7	8	0	1	0	327/7=46,7
0		429	8	2	0	0	1	429/8=53,6
∆		0	-6	-4	0	0	0

Так как не все элементы последней строки ≥ 0, то это не оптимальное решение. Находим ключевой столбец - , ключевую строку - , на пересечении ключевой элемент =7. Составляем новую симплекс-таблицу. вводим в базис, выходит из базиса. Ключевую строку делим на 7 и переписываем в новую таблицу. Умножаем ее на (-7) и складываем с первой, Умножаем ее на (-8) и складываем с 3-ей.

			6	4	0	0	0
0		36	0	5	1	-1	0	363/7=51,9
6		327/7	1	8/7	0	1/7	0	327/7=46,7
0		387/7	0	-50/7	0	-8/7	1	429/8=53,6
∆		1962/7	0	20/7	0	6/7	0

Так как все элементы последней строки ≥ 0, то это оптимальное решение.

=327/7=0

Необходимо изготовить 327/7 изд. А и не изготавливать изд. вида В

руб.

4. Решить транспортную задачу, заданную распределительной таблицей.

	40	20	40
30	3	1	3
25	5	4	2
15	4	3	5
30	1	5	5

Решение:

Проверим условие закрытости задачи:

Задача закрытая. Составим план методом наименьшей стоимости. Находим клетку с наименьшей стоимостью=1: клетки (1,2) и (4,1).Заполняем клетку (1,2)=min(30,20)=20. Исключаем из рассмотрения 2 столбец, так как потребности 2 потребителя удовлетворены. Заполняем следующую клетку (4,1)=min(30,40)=30. Исключаем из рассмотрения 4 строку, так как запасы 4 поставщика исчерпаны. Клетка (2,4) =min(40,25)=25, исключаем 2 строку и т.д.

Пункты отправления	Пункты назначения									Запасы
	3	-		10		1	3	+	0	30	0
						20
	5					4	2			25	-1
							25
	4		+		*	3	5	-	15	15	2
	1					5	5			30	-2
	30
Потребности	40					20	40
	3					1	3

Для занятых клеток подсчитаем потенциалы поставщиков и потребителей:

Положим , тогда, работая с занятыми клетками, получаем:

Для свободных клеток подсчитаем оценки :

, , ,

, , .

Так как среди чисел есть положительные (), то полученный план не является оптимальным.

Для клетки (3,1) строим цикл пересчета.

Пункты отправления	Пункты назначения			Запасы
	3	1	3	30	0
		20	10
	5	4	2	25	-1
			25
	4	3	5	15	2
	10		5
	1	5	5	30	-1
	30
Потребности	40	20	40
	2	1	3

Для занятых клеток подсчитаем потенциалы поставщиков и потребителей:

Положим , тогда, работая с занятыми клетками, получаем:

Для свободных клеток подсчитаем оценки :

, , ,

, , .

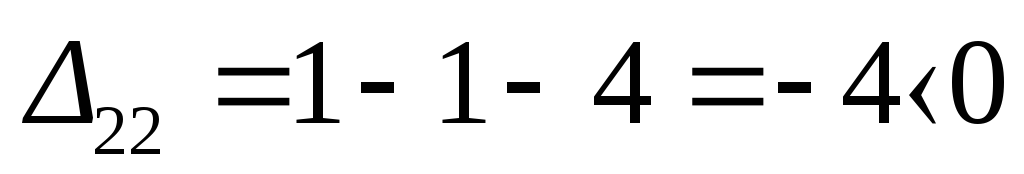Так как среди чисел нет положительных, то полученный план является оптимальным.

.

При данном плане транспортные расходы составляют:

5. Решить транспортную задачу. Заданы мощности поставщиков а_j (j = 1, 2, 3), емкости потребителей b_j (j = 1, 2, 3) и матрица стоимостей перевозок единицы продукции от каждого поставщика каждому потребителю. Требуется найти план перевозок, при котором суммарные транспортные затраты будут наименьшими.

аj	20	14	16
30	5	2	6
15	2	1	3
25	4	2	8