
- •Общее решение системы линейных уравнений
- •Транспонирование матриц и его свойства
- •Разложение произвольного вектора по ортам координатных осей на плоскости и в пространстве.
- •Действия с векторами в координатной форме
- •Признак коллинеарности векторов
- •Уравнение прямой, проходящей ч/з 2 точки на плоскости и в пространстве
- •Условия параллельности и перпендикулярности прямых
- •Окружность. Ее каноническое уравнение
- •Эллипс. Каноническое уравнение эллипса
- •Декартова сист-а координат в пространстве
- •У равнение прямой с угловым коэффициентом? Геометрический смысл углового коэффициента
- •Гипербола. Каноническое уравнение гиперболы
- •Парабола. Каноническое уравнение параболы
- •Понятие матрицы.Квадратная матрица
Нулевая матрица и ее свойства
Нулева́я ма́трица — это матрица, размера все элементы которой равны нулю. Ранг нулевой матрицы равен 0
![]()
Свойства:
1) Произведение нулевой матрицы на любое число равно ей самой
2) Сумма матрицы A и нулевой матрицы того же размера равна исходной матрице A
3) Разница матрицы A и нулевой матрицы того же размера равна исходной матрице A
4)произведение матрицы А на нулевую равно нулевой матрице
5) Квадр. нулевая матрица является вырожденной(т.е. ее определитель равен нулю).такие матрицы не имеют обратной матрицы
6)Квадратная нулевая матрица,её транспонированная матрица равна ей самой
7)Квадратная нулевая матрица является верхнетреугольной, нижнетреугольной и диагональной матрицей.
8) перестановочна с любой квадратной матрицей того же размера.
|
элементарные преобразования матриц и его свойства
Элем.преобр.матриц- это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц.
1) умножение какой-нибудь строки (столбца) на отличное от нуля число;
2) прибавление к какой-нибудь строке (столбцу) другой ее строки (столбца), умноженной на произвольное число;
3) перестановку местами любых двух строк (столбцов).
При помощи элементарных преобразований любую матрицу можно привести к матрице, у которой в начале главной диагонали стоят подряд несколько единиц, а все остальные элементы равны нулю. Такую матрицу называют канонической
4)вычеркивание (удаление) одной из одинаковых строк (столбцов)
5) транспонирование
Также
с помощью элементарных преобразований
строк квадратную матрицу А можно
привести к единичной матрице Е, то при
таких же элементарных преобразованиях
над матрицей Е получим А-1
![]()

 Правило
Крамера
Правило
Крамера
способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы. Назван по имени Габриэля Крамера.
Пример
1)дана Система линейных уравнений
![]()
2)найти определители(вставляем свободные члены(b) вместо каждой неизвест. переменной (х)
![]()
![]()
3)находим неизвестные числа (х)
![]()
Можно наверняка использовать формулы Крам,если:
1)столбцы или строки м.А линейно независимы(т.е. определитель м.А ≠0
2)ранг матрицы А равен числу неизвестных
Треугольная матрица и ее свойства
Треугольная матрица— квадратная матрица, в которой все элементы ниже или выше главной диагонали равны нулю. Бывают:
1)нижнетреугольная(все элементы выше главной диагонали равны нулю)
2)диагональная(по диагонали цифры, наверху внизу-нули)
 3)единичная
матрица
3)единичная
матрица

1 2 3 4 4)верхнетреугольная(все элементы ниже главн.
0 1 3 1 диагонали равны нулю)
0 0 2 1
0 0 0 3
Свойства:
1)Определитель треугольной матрицы равен произведению элементов на её главной диагонали
2)Определитель унитреугольной матрицы равен единице
3) При возведении треугольной матрицы в целую положительную степень ее диагональные элементы возводятся в эту же самую степень
4) При умножении треугольной матрицы на некоторое число ее диагональные элементы умножаются на это же самое число
Правило Саррюса (правило звездочки)
Используется для вычисления определителя 3 порядка
![]()
Теорема Кронеккера-Капелли
Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений.
1)если ранг основ м-ы системы = рангу расширенной м-ы, то система имеет хотя бы одно решение R(A)=R(A|B)
2)если ранг м.А равен рангу расширенной м-ы и равен числу неизвестных, то система определенна,т.е. имеет 1 решение R(A)=R(A|B)=n
3)если ранг м.А равен рангу расширенной матрицы и меньше числа неизвестных,то система имеет бесконечное множ-о решений R(A)=R(A|B)<n
4)если ранг основной ранг матрицы А не равен рангу расширенной, то система несовместна ,следовательно не имеет решений R(A) ≠ R(A|B)
R(A)=R(A|B)>n –ТАКОГО БЫТЬ НЕ МОЖЕТ
![]()
Зная число неизвестных(в примере их 3 шт),ранги обеих матриц-можем найти число свободных переменных по формуле n-R=c , а также число базисных переменных по формуле n-c
Найдя число свободных переменных,переносим их в сторону расширенной матрицы с противоположным знаком. Находим х1,х2,х3. Это и будет общим решением
Сложение матриц и его свойства
Суммой двух матриц одного размера называется матрица того же размера, каждый элемент которой равен сумме соответствующих элементов данных матриц.
![]()
![]()
Свойства сложения матриц
5.коммутативность(А+В=В+А))
6.ассоциативность (А+В)+С=А+(В+С)
7.сложение с нулевой матрицей(А+0=А)
8.существование противоположной матрицы А+(-А)=0
матричная запись системы линейных уравнений
рассмотрим систему уравнений:
![]()
![]() матрица
сист
матрица
сист
![]() матрицы-столбцы.(х-число
неизвестн,с-свободные члены) Очевидно,
что:
матрицы-столбцы.(х-число
неизвестн,с-свободные члены) Очевидно,
что:
![]() ,тогда
,тогда
АХ=С-такое равенство называют матричным уравнением.
Если матрица А системы невырожденная, (det А 0), то это уравнение решается следующим образом:
Для этого необходимо умножить обе части матричного уравнения на обратную матрицу (А-1). В левой части произведение обраной матрицы на матрицу коэффициентов дает единицу а в правой части как раз стоит произведение обратной матрицы на столбец свободных членов, которое и дает матричное решение системы линейных уранений.
Общее решение системы линейных уравнений
если общая система линейных уравнений АХ=В совместна, R(A)=R ,например
a11 a12 … a1r
a21 a22 … a2r11Equation Section (Next)
… … … …
ar1 ar2 … arr
есть базисный минор матрицы системы, то она равносильна системе
a11 x1 + a12 x2 + … + a1r xr = b1 – a1r+1 - … - a1n xn
a21 x1 + a22 x2 + … + a2r xr = b2 – a2r+1 - … - a2n xn
……………………………………………………………………………………….
ar1 x1 + ar2 x2 + … + arr xr = br – arr+1 - … - arn xn
Придавая переменным xr+1 , xr+2 , … , xn (свободным переменным произвольные значения xr+1 = cr+1, xr+2 = cr+2, …,xn= cn , получим однозначно (например,по правилу крамера) значения x1 = c1, x2=c2, …, xr=cr. Тогда (c1, c2, cn) является решением исходной матрицы
Транспонирование матриц и его свойства
Транспонированная матрица — матрица AT, полученная из исходной матрицы A заменой строк на столбцы.
Свойства:
1) (АТ)Т=А (Дважды транспонированная матрица А равна исходной матрице А)
2) (λА)Т= λАТ (При транспонировании можно выносить скаляр)
3) (А+В)Т=АТ+ВТ (Транспонированная сумма матриц равна сумме транспонированных матриц)
4) (АВ)Т=ВТ+АТ (Транспонированное произведение матриц равно произведению транспонированных матриц)
5) (Определитель транспонированной матрицы равен определителю исходной матрицы)
Полярная система координат— двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов.основными элементами этой системы явл. Точка отсчета(полюс) и луч,начинающейся в этой точке

 ρ
ρ
φ
луч
|
полюс
ρ-расстояние, φ-угол между полярной осью и отрезком,соединяющим точку А с полюсом. Полярный угол определен для любой точки плоскости, за исключением полюса , и принимает значения , -π<φ≤π , называемыми главными значениями полярного угла .
Полярный угол измеряется в радианах и отсчитывается от полярной оси:
- в положительном направлении (против направления движения часовой стрелки), если значение угла положительное;
- в отрицательном направлении (по направлению движения часовой стрелки), если значение угла отрицательное.
Формулы,связывающие декарт.и полярн.системы
Полярные координаты легко преобразовать в декартовы.
 для
перехода из декартовой в полярную
для
перехода из декартовой в полярную
 для
перехода из полярной в декартовую
для
перехода из полярной в декартовую
Деление отрезка в заданном соотношении
Если точка М(x; y) лежит на прямой, проходящей через две данные точки М1 (x1, y1) и M2(x2,y2), и дано отношение
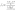 ,
в котором точка М делит отрезок М1М2
, то
координаты точки М определяются по
формулам:
,
в котором точка М делит отрезок М1М2
, то
координаты точки М определяются по
формулам:
![]()
![]()
Если точка М является серединой отрезка М1М2 , то ее координаты определяются по формулам:
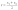
![]()
Если λ=0, то это означает , что точки А и М совпадают.
Если λ<0, то точка М лежит вне отрезка М1М2

М1 М М2
Понятие радиус-вектора
Радиус-вектор точки - это называется вектор, начало которого совпадает с началом системы координат, а конец - с данной точкой. Таким образом, особенностью радиус-вектора, отличающего его от всех других векторов, является то, что его начало всегда находится в точке начала координат. Можно определить расположение точки векторным способом. Если известен радиус-вектор данной точки, то и ее положение оказывается известным, поскольку точка конца радиус-вектора совпадает с данной точкой. Так, положение точки В - это конец ее радиус-вектора r1. Длина радиус-вектора, или его модуль, определяет расстояние, на котором точка находится от начала координат, а стрелка указывает направление на эту точку пространства.
На плоскости углом радиус-вектора называется угол, на который радиус-вектор повёрнут относительно оси абсцисс в направлении против часовой стрелки.







