
- •Электричество и магнетизм - учение об электромагнитном взаимодействии и поле
- •Электростатика, ее предмет и основные понятия. Электрический заряд и его свойства.
- •Закон Кулона. Характер сил электростатического взаимодействия точечных зарядов и основные характеристики и уравнения электростатического поля.
- •Форма закона Кулона
- •Методы расчета основных характеристик электростатического поля.
- •Использование закона Кулона и принципа суперпозиции для расчета напряженности эсп электрического диполя.
- •А) Напряженность эсп диполя в точках вдоль его ocи.
- •Б) Напряженность эсп диполя в точках на срединном перпендикуляре к его оси.
- •2. Применение теоремы Остроградского-Гаусса к расчету характеристик эсп симметричных, равномерно заряженных тел.
- •А ) сфера
- •Б) бесконечно длинная прямолинейная нить (цилиндр).
- •В) бесконечная равномерно заряженная плоскость.
- •Г) конденсатор (плоский).
- •Внешние проявления эсп. Взаимодействие эсп с вещественными средами.
- •Сила и ее работа при действии на точечный заряд. Энергия заряженного проводника. Энергия взаимодействия зарядов.
- •Момент силы и его работа при действии эсп на электрический диполь.
- •Взаимодействие эсп с диэлектриками. Полярные и неполярные диэлектрики. Поляризация. Поляризованность (вектор поляризации). Диэлектрическая проницаемость.
- •Теорема Остроградского - Гаусса для диэлектрика. Граничные условия.
- •Взаимодействие эсп с проводящими средами.
- •Электроемкость проводника. Конденсаторы.
- •Энергия заряженного конденсатора и проводника. Объемная плотность энергии эсп.
- •Сторонние силы. Электродвижущая сила. Закон Ома для неоднородного участка цепи и для замкнутой цепи. Эдс, напряжение и разность потенциалов.
Теорема Остроградского - Гаусса для диэлектрика. Граничные условия.
Источниками ЭСП служат как свободные (сторонние) заряды q, так и связанные заряды q в диэлектрике. Поэтому теорема Остроградского-Гаусса для диэлектрика должна быть записана в следующем виде:
=
![]() = (q + q
)/о
= (q + q
)/о
В

![]() при неоднородной поляризации
диэлектрика внутрь объема V;
при неоднородной поляризации
диэлектрика внутрь объема V;
dq = dS = - РndS.
Знак
"минус" указывает на поступление
заряда внутрь объема V, т. е. в направлении
противоположном внешней нормали
к площадке d
.
Через всю поверхность S внутрь объема
V при поляризации диэлектрика поступает
заряд q
=
-![]() .
Подставляя это выражение в формулу
теоремы Остроградского-Гаусса, после
преобразований получаем:
.
Подставляя это выражение в формулу
теоремы Остроградского-Гаусса, после
преобразований получаем:
![]() = q
= q![]()
![]() = q
= q
Поток вектора электрического смещения через любую замкнутую поверхность не зависит ни от размера, ни от формы поверхности, а определяется лишь суммарным свободным (сторонним) зарядом, находящимся внутри замкнутой поверхности, будучи численно равным этому заряду. В этом заключается суть теоремы Остроградского-Гаусса для диэлектрика. Этим, в основном и оправдывается введение дополнительного (вспомогательного) вектора , облегчающего расчет вектора в диэлектрических и особенно в неоднородных средах и связанном с ним следующим соотношением: Dn = оЕn + Pn или = о + = о .
Три вектора: , и по разному характеризуют силу ЭСП. Вектор определяется только связанными зарядами так, что его нормальная составляющая равна поверхностной плотности связанного (поляризационного) заряда в диэлектрике: Рn = . Аналогично вектор определяется только свободными зарядами и его нормальная составляющая равна поверхностной плотности свободного заряда: Dn = . Вектор определяется как свободными, так и связанными зарядами.
В
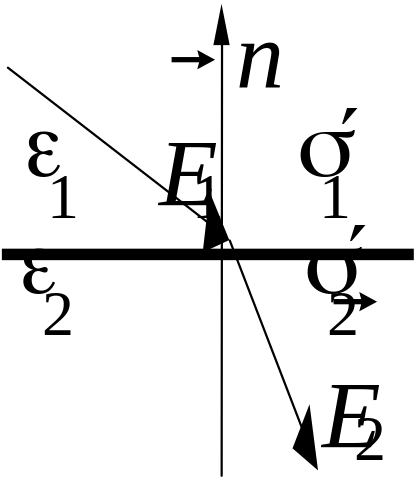
Г
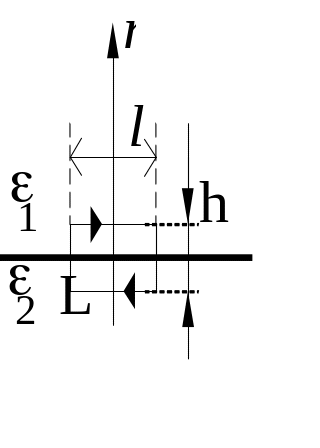
Выберем в качестве замкнутого контура L вытянутый вдоль границы раздела двух диэлектриков прямоугольник малой высоты h, длинные стороны l которого находятся по разные стороны от границы (в разных диэлектриках). Циркуляция вектора должна быть равна нулю, то есть Е1l - Е2l = 0, где Е1 и Е2 - касательные составляющие вектора Е к границе раздела в первом и втором диэлектрике, соответственно. Очевидно, что Е1 = Е2, то есть касательная составляющая вектора проходит границу раздела двух диэлектриков не изменяясь. Касательная же составляющая вектора = о будет испытывать на границе раздела диэлектриков разрыв, ибо из Е1 = Е2 D1/о1 = D2/о2 D1/D2 = 1/2.
Д

![]() =
q, выберем в качестве замкнутой поверхности
для вычисления потока ФD
вектора
электрического смещения цилиндр малой
высоты h, ось которого нормальна к границе
раздела, а его основания площадью S
располагаются симметрично по разные
стороны от границы раздела, то есть в
разных диэлектриках. Полагая, что граница
диэлектриков не содержит свободных
(сторонних) зарядов (q = 0), получим, что
поток вектора
через основания цилиндра равен: Dn1S
- Dn2S
= 0, откуда следует, что нормальная
составляющая вектора
на границе
раздела двух диэлектриков остается
неизменной Dn1
= Dn2.
Нормальная же составляющая вектора
напряженности
=
/о
испытывает на границе раздела диэлектриков
разрыв, скачок: из Dn1
= Dn2
=
q, выберем в качестве замкнутой поверхности
для вычисления потока ФD
вектора
электрического смещения цилиндр малой
высоты h, ось которого нормальна к границе
раздела, а его основания площадью S
располагаются симметрично по разные
стороны от границы раздела, то есть в
разных диэлектриках. Полагая, что граница
диэлектриков не содержит свободных
(сторонних) зарядов (q = 0), получим, что
поток вектора
через основания цилиндра равен: Dn1S
- Dn2S
= 0, откуда следует, что нормальная
составляющая вектора
на границе
раздела двух диэлектриков остается
неизменной Dn1
= Dn2.
Нормальная же составляющая вектора
напряженности
=
/о
испытывает на границе раздела диэлектриков
разрыв, скачок: из Dn1
= Dn2
о1Еn1 = о2Еn2 Еn1/Еn2 = 2/1.
Полученные граничные условия для касательной и нормальной составляющих векторов и позволяют выявить характер преломления линий и на границе раздела двух диэлектриков. Обозначив углы падения этих векторов на границу раздела за и , а углы преломления за и , имеем:
tg = Е1/Еn1, а tg = Е2/Еn2, откуда tg /tg = (Е1/Еn1)/(Е2/Еn2) = (Е1/Е2)(Еn2/Еn1) = Еn2/Еn1 = 1/2.
Отсюда tg = (2/1)tg .
Эта
формула выражает закон преломления
силовых линий ЭСП на незаряженной
поверхности однородных изотропных
диэлектриков. При переходе в среду с
большей диэлектрической проницаемостью
(2
1)
угол преломления
оказывается больше угла падения ,
то есть вектор
![]() отклоняется от нормали по отношению к
вектору
в первой среде.
отклоняется от нормали по отношению к
вектору
в первой среде.
Повторив подобные выкладки для вектора , имеем:
tg /tg = (D1/Dn1)/(D2/Dn2) = (D1/D2)(Dn2/Dn1) = (D1/D2) = 2/1. Для вектора получили результат, подобный тому, который был получен для вектора .
