Питання для самоконтролю

1. Що вивчає предмет статики?

2. Що називається силою і якими факторами характеризується дія сили на тверде тіло?

3. Що складає систему сил і які системи називаються еквівалентними?

4. Що розуміють під рівновагою тіла?

5. Яка сила називається рівнодійною даної системи сил?

6. Яке тіло називається абсолютно твердим?

7. Як формулюються аксіоми статики?

8. Що називається в'яззю і силою реакції в'язі?

9. В чому полягає принцип звільнення від в'язей?

10. В чому полягає теорема "про три сили"?

11. Які дві основні задачі розглядаються в статиці?

1.3.2. Методика розв'язання задач статики

При розв'язанні задач слід дотримуватися наступної послідовності:

1. Визначити тіло, рівновагу якого слід розглянути в даній задачі.

2. Показати на рисунку всі активні сили, які діють на вибране тіло.

3. Звільнити від в'язей вибране тіло і замінити їх дію силами реакцій в'язей. Зобразити у вигляді векторів усі сили реакцій відкину­тих в'язей.

4. Скласти рівняння, яке б виражало умови рівноваги тіла. Тип цих рівнянь визначається характером сил, що діють на тіло.

Зокрема, при розв'язуванні задач з теми "Плоска система збіж­них сил" з використанням геометричної умови рівноваги необхідно побудувати замкнутий силовий трикутник. Його побудову необхідно починати з відомої сили, далі за відомими елементами трикутника знайти невідомі величини. Якщо силовий трикутник косокутний, то при розв'язуванні корисно використати теорему синусів, але інколи доцільним є використання умови пропорційності сторін двох подібних трикутників (силового трикутника і трикутника за основним рисун­ком).

Задача 1.1.

Балка, вагою якої нехтують, шарнірно закріплена на опорі А, кінцем В покладена на котки. На балку діє вертикальна сила , яка дорівнює 100 Н. Взявши розміри з (рис. 1.10), визначити реакції опор і .

Розв'язання

1. Розглянемо рівновагу балки АВ (рис. 1.11).

2. Покажемо силу ( - активна сила).

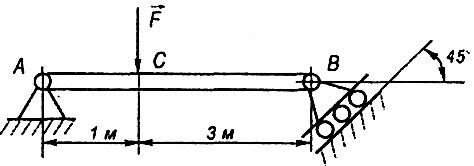
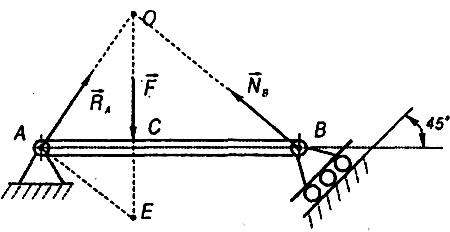
Рис. 1.10 Рис. 1.11

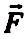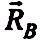3. Звільнимо балку АВ від в'язей, які накладені на неї. Нерухомий ша­рнір А і опора на катках В - це в'язі. Реакція перпендикулярна опорній поверхні. Для знаходження лінії дії реакції шарніра А застосовуємо теорему про три непаралельні сили і знаходимо точку О перетину ліній дії сил і , а потім точку О з'єднуємо з точкою А. Це буде лінія дії реакції 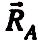. На­прям реакції знаходимо із замкнутого силового трикутника.

4. Будуємо силовий трикутник. Для цього з довільної точки на пло­щині відкладаємо в масштабі силу 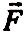, з кінця і початку якої проводимо прямі, паралельні лініям АО і БО.

5. Одержуємо замкнутий силовий трикутник KDM (рис. 1.12). За умови замкнутості силового трикутника виводимо, що реакція 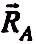направлена до точки О (реакцію 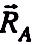показуємо на рис. 1.11).

6. Р

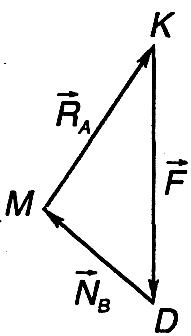
   Рис. 1.12

   озв'язуємо силовий трикутник. В нашому випадку для розв'язу­вання трикутника даних недостатньо, тому будуємо відомий трикутник, поді­бний силовому трикутнику. Трикутник АОЕ подібний трикутнику KDM. З подібності трикутників маємо:

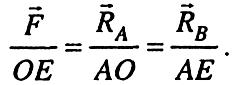
З рис. 1.11 легко знаходимо, що ОЕ=4 м,

м,. м.

Звідки:

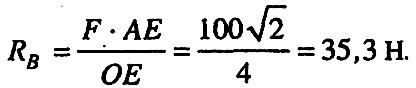
Рис. 1.13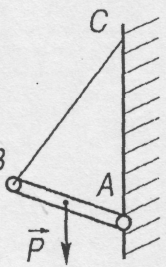

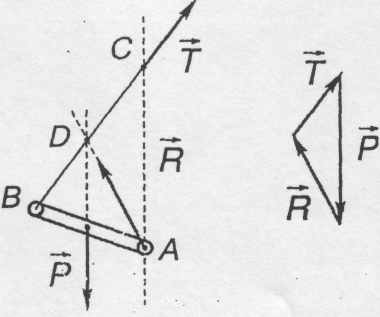
Задача 1.2

Однорідна балка вагою Р утримується в рівно­вазі ниткою ВС і шарніром А (рис. 1.13). Знайти натяг нитки і реакції шарніра А, якщо

Розв'язання:

Розглянемо рівновагу балки з ниткою. Звільни­мо систему від в'язей в точках А і С та прикладемо в цих точках сили реакції (рис. 1.14). Система трьох сил – сили ваги (прикладена в середині балки), сили натягу і реа­кція шарніра повинні бути еквівалентними нулеві. За теорією про три сили реакція повинна проходити че­рез точку D (середину сторони ВС).

Будуємо силовий трикутник. З подібності силового трикутника і три­кутника ADC (рис. 1.14) випливає:

Нехай АС=21, тоді

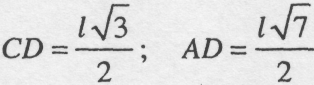
Звідси отримуємо:

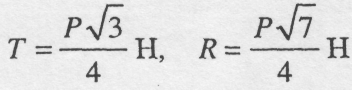
Задача 1.3

Тюбінг радіусом R см і вагою Р = 2 кН накочується на виступ висотою h = +2R см (рис. 1.15. а). Визначити силу , яка направлена під кутом 45° до горизо­нту, необхідну для переміщення тюбінга через виступ. Перекочування тюбінга почи­нається при такій силі . коли сила реакції опори в точці В дорівнює нулю.

Розв'язання

Рис. 1.14

Для визначення сили необхідно розглянути рівновагу трьох сил, прикладених до тюбінга (рис. 1.15. б) – сили _, сили ваги і сили реакції виступу . Сила реакції направлена за нормаллю до поверхні тюбінга, тобто за його радіусом. Будуємо силовий три­кутник, який при рівновазі має бути замкненим (рис. 1.15, в). Сила є відо­мою стороною силового трикутника. Другий бік трикутника - починається в кінці вектора і складає з ним кут 60°. Шукана сила напра­влена під кутом 45° до горизонту і є третім боком силового трикутника.

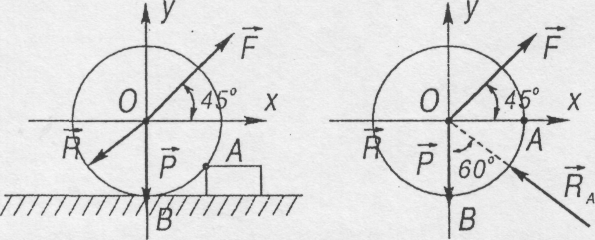
а) б) в)

Рис. 1.15

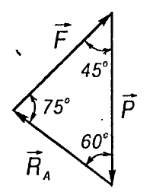
Проведемо через початок вектора лінію, паралельну силі , а че­рез кінець - лінію, паралельну силі . В результаті побудований замкнутий силовий трикутник, сторони якого дорівнюють силам, діючим на тюбінг.

За теоремою синусів для трикутника складемо рівняння:

Звідси знаходимо F=1,79KH, R_A =1,46кН.

РОЗДІЛ 2. СИСТЕМА ЗБІЖНИХ СИЛ