Лекция 8

Среднеквадратичное приближение

Однако в ряде случаев выполнение условия совпадения аппроксимирующей функции со всеми точками аппроксимируемой функции затруднительно или даже нецелесообразно.

Например, при большом количестве узлов интерполя­ции получается высокая степень многочлена, т. е. когда нужно иметь один интерполяционный многочлен для всего интервала изменения аргумента. Выход из этого положения может быть найден выбором такого многочлена, график которого проходит близко от данных точек ( рисунок. 8.1., штриховая линия). Понятие «близко» уточняется при рассмотрении разных видов прибли­жения.

Одним из таких видов является среднеквадратичное приближение функций с помощью многочлена (7.1). На практике стараются подобрать аппроксимирую­щий многочлен как можно меньшей степени (как прави­ло, m = 1, 2, 3).

Мерой отклонения многочлена φ(х) от заданной функции у = f (х) на множестве точек (х_і, у_і) (і = 0, 1, ... ..., п) при среднеквадратичном приближении являе тся величина Ѕ, равная сумме квадратов разностей между значениями многочлена и функции в данных точках:

Ѕ = ∑[ φ (х) - у]². (8.1)

Для построения аппроксимирующего многочлена нужно подобрать коэффициенты а₀, . . ., а^m, так, чтобы вели­чина S была наименьшей.

Равномерное приближение.

Во многих случаях, особенно при обработке экспериментальных данных, среднеквадратичное приближение вполне приемлемо, по­скольку оно сглаживает некоторые неточности функции у = f (х) и дает достаточно правильное представление о ней. Иногда, однако, при построении приближения ставится более жесткое условие: требуется, чтобы во всех точках некоторого отрезка [а, в] отклонение многочлена φ (χ) от функции f (х) было по абсолютной величине меньшим заданной величины ε > 0:

|f(x) — φ (х)| < ε, a ≤ х ≤ b (8.2)

В этом случае говорят, что многочлен равномерно аппроксимирует функцию f(x) с точностью ε на отрез­ке [а, в].

Введем понятие абсолютного отклонения Δ многочле­на φ (χ) от функции j(x) на отрезке [а, Ь]. Оно равно максимальному значению абсолютной величины разности между ними на данном отрезке:

Δ = max |f(x) — φ (х)| < ε, (8.3)

По аналогии можно ввести понятие среднеквадратич­ного отклонения Δ = √Ѕ/n при среднеквадратичном при­ближении функций. На рис. 8.1 показано принципиальное различие двух рассматриваемых приближений.

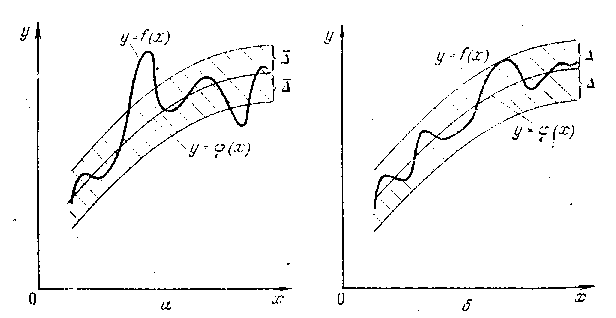
Рисунок 8.1- Среднеквадратичное (а) и равномерное (б) приближения.

Лекция 9

Линейное и квадратичное интерполирование функции.

Линейная интерполяция

1. Простей­шим и часто используемым видом локальной интерпо­ляции является линейная интерполяция. Она состоит в том, что заданные точки (x_і, y_i) (і = 0, 1, ..., п) соединяются прямолинейными отрезками, и функция f(x) приближается ломаной линией с вершинами в данных точках.

Уравнения каждого отрезка ломаной в общем случае разные. Поскольку имеется п интервалов (x_і-1 , x_і), то для каждого из них в качестве уравнения интерполя­ционного многочлена используется уравнение прямой, проходящей через две точки. В частности, для і-го ин­тервала можно написать уравнение прямой, проходящей через точки (x_і-1, y_i-1 ) и (, y_i), в виде

, из которого следует ; , (9.1)

где ; .

Следовательно, при использовании линейной интерполяции сначала нужно определить интервал, в который попадает значение аргумента х, а затем подставить его в формулу (9.1) и найти приближенное значение функции в этой точке.

Блок схема алгоритма вычисления приближенного значения функции методом линейной интерполяции показана на рис.9.1.

Квадратичная интерполяция

В качестве интерполяционной функции па от­резке [x_і-1, x_і+1] принимается квад­ратный трехчлен. Такую интерполя­цию называют также параболической. Уравнение квадратного трехчлена

y = α_ix² + b_ix +c_i x_і-1 ≤ x ≤ x_і+1 (9.2)

содержит три неизвестных коэффи­циента α_i, b_i, c_i, для определения которых необходимы три уравнения. Ими служат условия прохождения параболы (9.2) через три точки (x_і-1, y_i-1 ), (x_і, y_i ), (x_і+1, y_i+1 ). Эти условия можно записать в виде

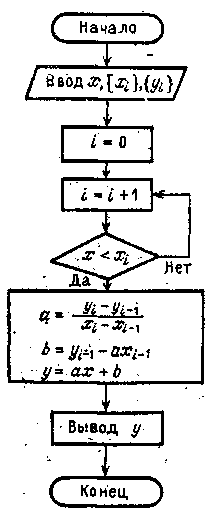
Рисунок 9.1. - Блок-схема линейной интерполя­ции

α_i x² _і-1+ b_i x_і-1+c_i = y_i-1 ,

α_i x² _і + b_i x_і + c_i = y_i , (9.3)

α_i x² _і+1+ b_i x_і+1+c_i = y_i+1 .

Алгоритм вычисления - приближенного значения функции с помощью квадратичной интерполяции можно представить в виде блок-схемы, как и для случая ли­нейной интерполяции. Вместо формулы (9.1) нужно использовать (9.2) с учетом решения си­стемы линейных уравнений (9.3). Интерполяция для любой точки x проводится по трем ближайшим к ней узлам.

Лекция 10

Глобальная интерполяция.

Более полное интерполирование (приближение) осуществляется в случае глобальной интерполяции. В этом случае строится интерполяционный многочлен, единый для всего отрезка . При этом, естественно, график интерполяционного многочлена должен проходить через две заданные точки.

Запишем исконный многочлен в виде:

(10.1)

Из условия равенства значений этого многочлена в узлах соответствующим заданным табличным значениям получим следующую систему уравнений для нахождения коэффициентов :

(10.2)

…………………..

Эта система имеет единственное решение, если среди узлов интерполяции нет совпадающих, т.е. когда . Решив эту систему, найдем коэффициенты интерполяционного многочлена (10.1). Однако такой путь построения интерполяционного многочлена требует значительного объема вычислений, особенно при большом числе узлов.

Многочлен Лагранжа.

Найдем более простой алгоритм построения интерполяционного многочлена. Для этого представим многочлен (10.2) в виде линейной комбинации многочленов степени n:

(10.3)

При этом принимаем условие, что каждый многочлен обращается в нуль во всех узлах интерполяции, за исключением одного (i-го), где он должен равняться единице. Таким условиям отвечает многочлен вида (для узла ):

(10.4)

Действительно, при ; при числитель выражения (10.4) обращается в нуль. По аналогии с выражением (10.4) получаем:

Для узла (10.5)

Для i-го узла (10.6)

Подставляя в многочлен (10.3) выражения (10.4, 10.5, 10.6) находим

(10.7)

Эта формула называется интерполяционным многочленом Лагранжа.

Лекция 11

Численное интегрирование.

Понятие интегральной суммы.

Если на отрезке [a,b] задана функция y=f (x). Разбиваем отрезок [a,b] с помощью точек на n элементарных отрезков [ ] (i=1,2,…,n), причем ; .

На каждом из этих отрезков выберем произвольную точку ε . Она находится между крайними точками отрезка, т.е. и найдем произведение значения функции в этой точке на длину элементарного отрезка

(11.1)

Сумма всех произведений на отрезке [a,b] для всех точек будет

(11.2)

Сумма называется интегральной суммой.

Определенный интеграл функции на заданном отрезке.

Определенным интегралом от функции f(x) на отрезке [a,b] называется предел интегральной суммы при неограниченном увеличении точек разбиения; при этом длина наибольшего из элементарных отрезков стремится к нулю:

(11.3)

Считается, что если функция f(x) непрерывна на всем отрезке [a,b], то предел интегральной суммы существует и не зависит от способа разбиения отрезка [a,b] на элементарные отрезки, ни от выбора точек.

Геометрический смысл определенного интеграла.

На рисунке 11.1 показана функции f(x) на отрезке [a,b], которая разбита на n число отрезков произвольно длины.

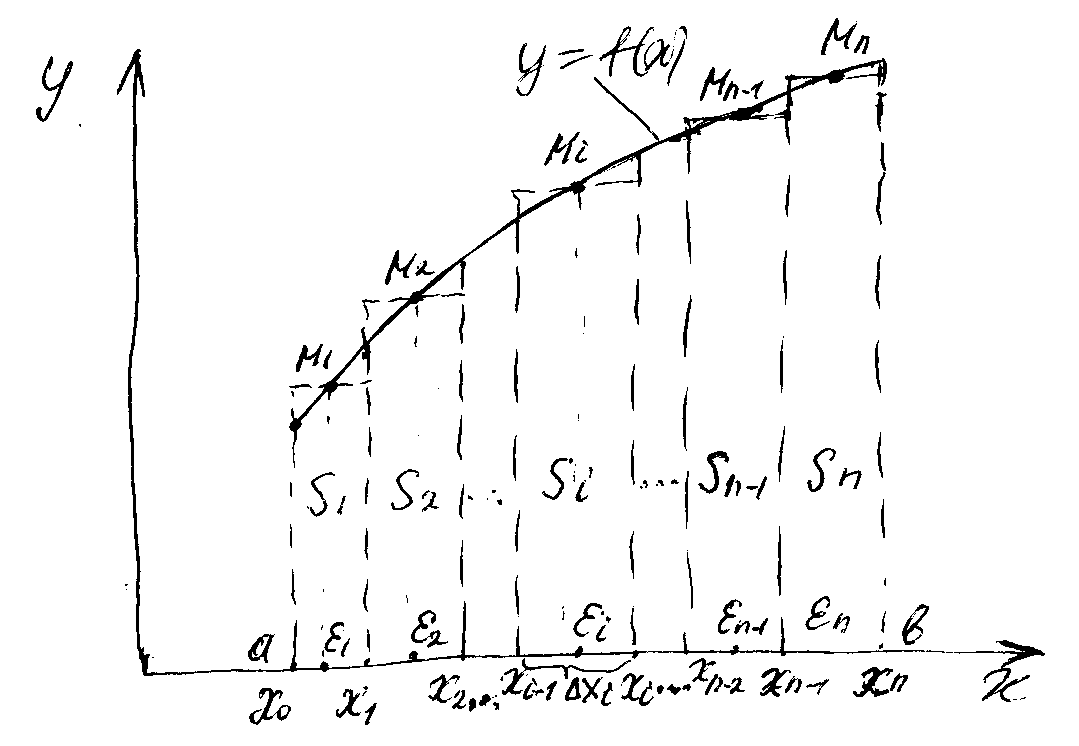
Рисунок 11.1- Геометрический смысл определенного интеграла

Абсциссами точек являются , ординатами , (см. рис.11.1). Выражение (11.1) описывает площадь элементарного прямоугольника. Выражение (11.2) описывает площадь ступенчатой фигуры, образуемой этими прямоугольниками.

При неограниченном увеличении числа точек деления и стремлении к нулю всех элементарных отрезков верхняя граница фигуры (ломаная линия) переходит в линию y=f (x). Площадь фигуры, которую называют криволинейной трапецией, равна определенному интегралу (11.3).

Вычисление определенного интеграла методом прямоугольников.

В основе методов численного интегрирования лежит замена определенного интеграла интегральной суммой (11.2). Численными методами решаются многие практические задачи: вычисление площадей сложных фигур, работы переменной силы, расход энергии и др.

Наиболее простым вариантом является метод прямоугольников. Он непосредственно использует замену определенного интеграла интегральной суммой прямоугольников (11.2), как показано на рис.11.2. В качестве точек ε могут выбираться левые или правые границы элементарных отрезков. Обозначив , а получаются следующие формулы метода прямоугольников.

Ошибка расчета из-за неучтенной площади треугольников с

криволинейной стороной.

Для левого способа:

Рисунок 11.2- Пояснение к методу прямоугольников.

(11.4)

Для правого способа формула имеет вид

(11.5)

В этом случае получается завышение площади.

Более точным способом является вид формулы, использующей значения в средних точках элементарных отрезков (полуцелых узлах):

(11.6)

где , .

По-другому этот метод называется метод средних. При этом лишний треугольник слева компенсируется недостающим треугольником справа, и точность расчета возрастает.

Лекция 12

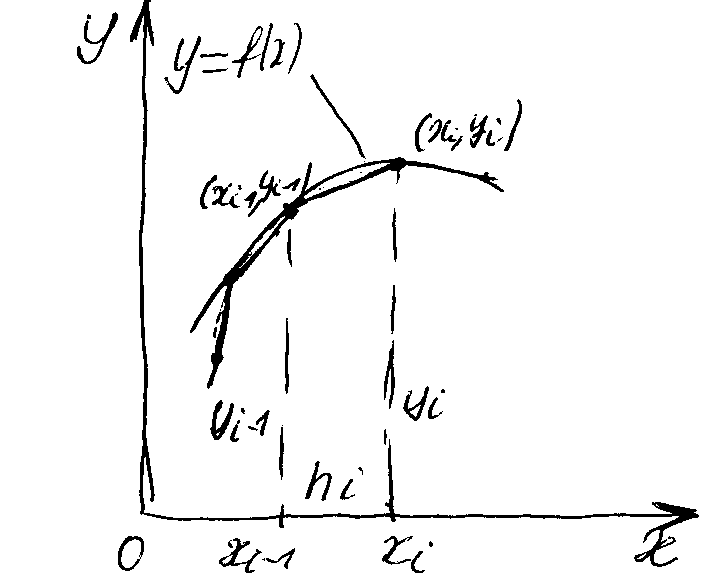
Вычисление определенного интеграла методом трапеций.

Метод трапеций основан на использовании линейной интерполяции. В этом случае график функции y=f (x) представляется в виде ломаной линии, соединяющей точки , т.е. все узлы интерполяции. Соседние узлы

Рисунок 12.1- Пояснение метода трапеций.

соединяются отрезками прямой (рис. 12.1). Тогда площадь криволинейной трапеции складывается из площадей элементарных прямолинейных трапеций. Площадь каждой элементарной трапеции равна произведению полусуммы оснований на высоту:

, . (12.1)

Складывая площади элементарных трапеций, получаем определенный интеграл и формулу для численного интегрирования

(12.2)

Численное интегрирование методом прямоугольников и трапеций с постоянным шагом.

Если отрезки разбиения сделать равными, то получаем постоянный шаг . Формулы численного интегрирования будут выглядеть так:

методом прямоугольников (12.3)

методом трапеций (12.4)

Для уменьшения погрешности необходимо увеличивать шаг разбиения. Но это возможно не всегда. Если функция задана в табличном виде, то шаг разбиения нельзя изменить. Тогда увеличить точность вычисления можно, используя другой метод численного решения.

Метод Симпсона.

Он основан на использовании квадратичной интерполяции. Разбиваем отрезок интегрирования [a,b] на четное число n равных частей с шагом . На каждом отрезке , (рис.12.1) подынтегральную функцию f(x) заменим интерполяционным многочленом второй степени:

(12.5)

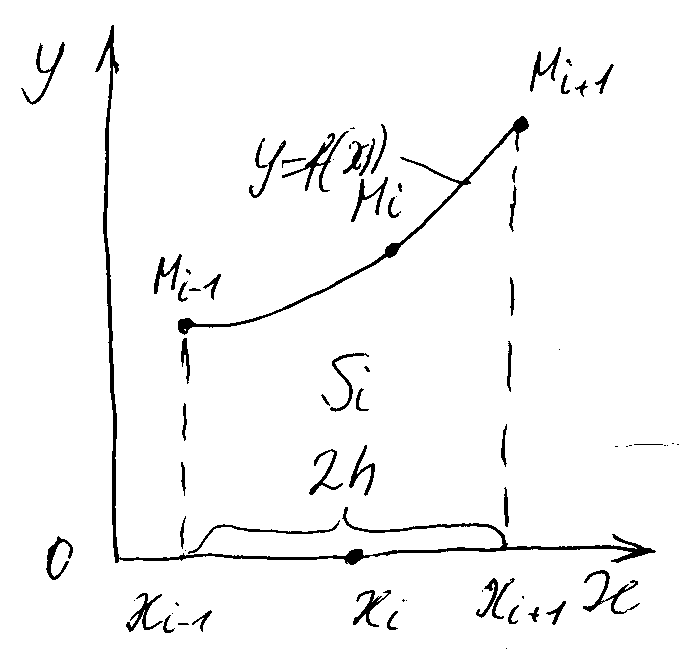
Рисунок 12.2- Пояснение схемы разбиения отрезка функции.

Для интерполяции используем

т.е. три узла. Коэффициенты этих квадратных трехчленов могут быть найдены из условий равенства многочлена в точках соответствующим табличным данным . В качестве интерполирующего многочлена можно использовать многочлен Лагранжа второй степени, проходящий через точки

(12.6)

Элементарная площадь может быть найдена с помощью определенного интеграла. Принимаем равенство и получаем

(12.7)

Проведя такие вычисления для каждого элементарного отрезка , просуммируем полученные выражения (12.7) для n элементарных отрезков:

(12.8)

Так как (12.8) является интегральной суммой, то можно записать

(12.8)

Полученное выражение называется формулой Симпсона.

Вычисления определенного интеграла по формуле Симпсона дают наиболее точный результат (по сравнению с методом прямоугольников и трапеций).

Блок-схема метода Симпсона.

(Выносится на самостоятельное изучение )

В качестве исходных данных задаются границы отрезка интегрирования погрешность , а также формула для вычисления подынтегральной функции .

Первоначально отрезок [a,b] разбивается на 4 части с шагом Вычисляется значение интеграла . Потом число шагов удваивается, вычисляется значение интеграла с шагом . Условие окончания счета принимается в виде . Если это условие не выполнено, то происходит новое деление шага пополам и т.д.

Рисунок 12.2- Блок-схема метода Симпсона.

Лекция 13

Численные решения нелинейных уравнений.

В различных областях научных исследований встречаются задачи, для решения которых необходимо найти корни нелинейных уравнений вида .

Существуют прямые и итерационные методы решения таких уравнений. Встречающиеся на практике нелинейные уравнения обычно не удается решить прямыми методами. Для решения таких задач оптимальными являются методы итераций, т.е. методы последовательных приближений.

Метод деления отрезка пополам (бисекции).

Это один из самых простых методов нахождения корней нелинейных уравнений. Корень функций находится в точке, при которой функция равна нулю. Допустим, имеется отрезок [a,b], в котором расположено искомое значение корня x=С, как показано на рисунке 13.1. Следовательно а< С <b. По этому методу в качестве начального приближения корня принимается середина отрезка:

. (13.1) Далее исследуем значение функции на концах отрезков

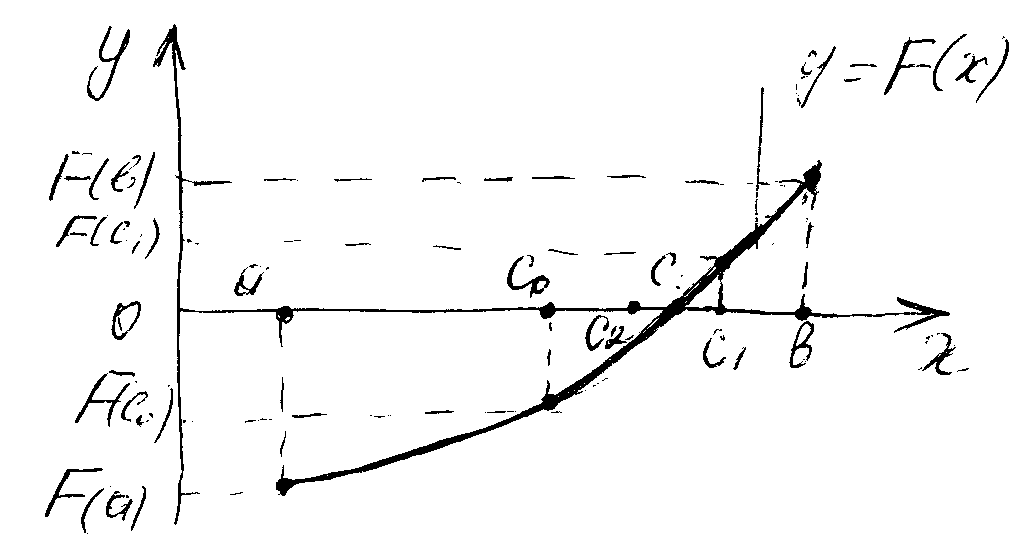
[a,с ] и [с ,b], т.е. в точках а, с , b (см.рис. 13.1).

Рисунок 13.1 - Метод деления отрезка пополам.

Тот отрезок, на концах которого принимает значения разных знаков, содержит искомый корень, поэтому он принимается в качестве нового отрезка. Вторую половину, на которой знак функции не меняется, отбрасываем. В качестве первой итерации корня принимаем середину нового отрезка. Затем процесс повторяется. Таким образом, после каждой итерации отрезок, на котором расположен корень, уменьшается вдвое. После n итераций он уменьшится в 2 раз.

Определяем знак функции в точках а, , b (см. рис. 13.1). Получаем F(а) < 0, F(с ) < 0, F(b) > 0. Изменение знака происходит на отрезке [с ,b], т.к. а . Поэтому следующий отрезок для приближения будет [с ,b], а приближение

(13.2) Теперь отрезок [с ,b] отбрасываем, т.к. и . Искомый корень . Затем аналогично находим и т.д. Итерационный процесс продолжается до тех пор, пока значение функции после n итераций не станет меньшим по модулю некоторого заданного малого числа ε, т.е. . Можно ограничивать число итераций по длине отрезка, когда она станет меньше допустимой погрешности.