Итерационные методы.

Итерационные методы – это методы последовательных приближений. В них необходимо задать некоторое приближенное решение – начальное приближение. После этого с помощью некоторого алгоритма проводится один цикл вычислений, называемый итерацией. В результате итерации находят новое приближение. Итерации проводятся до получения решения с заданной точностью. Алгоритмы решения линейных систем с использованием итерационных методов обычно сложнее по сравнению с прямыми методами. Объем вычисления при таком методе заранее определить трудно.

Тем не менее, итерационные методы чаще оказываются предпочтительнее благодаря следующим преимуществам:

- требуется хранить в оперативной памяти ЭВМ не всю матрицу системы, а лишь нескольких векторов с n числом элементов. Можно элементы матрицы не хранить, а вычислять по мере необходимости;

- погрешности результатов вычислений не накапливаются, поскольку точность вычислений в каждой итерации определяется лишь результатами предыдущей итерации и практически не зависит от ранее выполненных вычислений.

Эти достоинства итерационных методов позволяют использовать их в случае числа уравнений, а также для плохо обусловленных систем. Эти методы можно использовать для уточнения или проверки решений, полученных прямыми методами.

Способы решений прямыми методами.

Способ решения системы линейных уравнений по правилу Крамера.

Он основан на том, что каждое неизвестное представляется в виде отношений определителей.

Для системы двух уравнений с двумя неизвестными

; ;

, , (4.1)

Это правило можно использовать и для решения систем уравнений произвольного порядка. Однако при большом числе уравнений потребуется выполнить огромное количество арифметических действий, т.к. для n числа неизвестных надо найти значения n+1 числа определителей. Вычисление каждого определителя в свою очередь требует (n-1)n! умножений и n!-1 сложений. Поэтому это правило используют при решении систем, состоящих из небольшого числа уравнений.

Лекция 5

Способ решения системы по методу Гаусса.

Прямой ход метода Гаусса.

Этот метод является наиболее распространенным для решения систем линейных уравнений. Он основан на приведении матрицы системы к треугольному виду. Это достигается последовательным исключением неизвестных из уравнений системы. Сначала с помощью первого уравнения исключается из всех последующих уравнений системы. Затем с помощью второго уравнения исключатся из третьего и последующих уравнений. Этот процесс называется прямым ходом метода Гаусса. Продолжается он до тех пор, пока в левой части последнего (n-го) уравнения не останется лишь один член с неизвестным . Это значит, что матрица системы приведена к треугольному виду. Метод Гаусса применяется только к невырожденным матрицам.

Рассмотрим применение этого метода для системы:

,

, (5.1)

.

Для исключения из второго уравнения прибавим к нему первое, умноженное на - . Затем, умножив первое уравнение на - , прибавим его к третьему уравнению, исключая из третьего уравнения. Получим равносильную систему уравнений вида:

,

, (5.2)

,

где , ,

,

, ,

.

Теперь из третьего уравнения исключаем , умножив второе уравнение на - и прибавив результат к третьему. Получаем систему уравнений вида:

,

, (5.3)

,

где , .

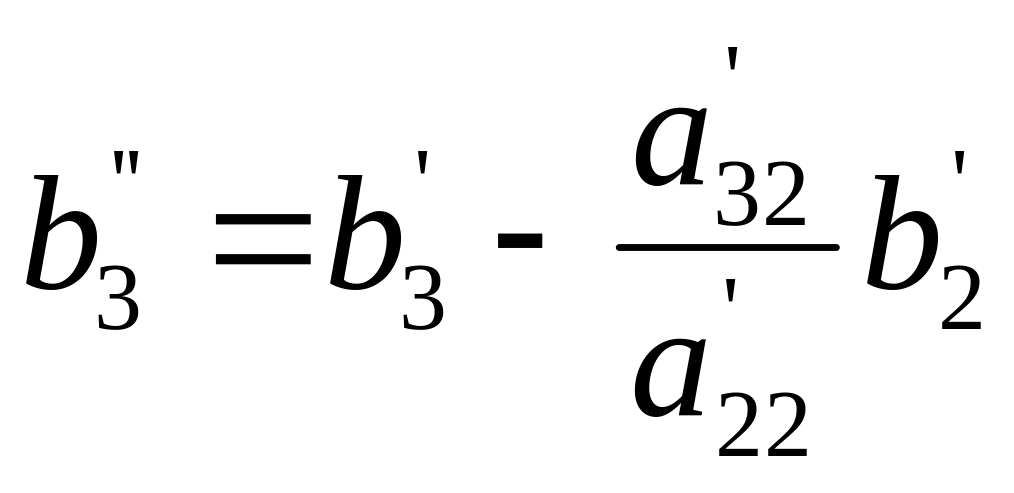Матрица системы уравнений (5.3) имеет треугольный вид. На этом заканчивается прямой ход метода Гаусса. Так как в процессе исключения неизвестных приходится делить на коэффициенты , то они должны отличаться от нуля.