1. Асимптоты графика ф-ции.

Точки в которых нарушается непрерывность ф-ции, назыв. точками разрыва этой ф-ции. Точка разрыва ф-ции назыв. Точкой разрыва 1-го рода, если в ней ф-ция имеет конечный левый и правый пределы. Все остальные точки разрыва назыв. Точками разрыва 2-го рода.

Асимптота-это прямая линия, к которой приближается график ф-ции при подходе Х в точке разрыва 2-го рода или при удалении в +/- ∞.

Асимптоты бывают:

а) вертикальные в точках разрыва 2-го рода

б) наклонные у=kх+b, где

k=lim ____

b=lim (f(x)-kx)

в) если k=0, то асимптота становится горизонтальной

Общая схема исследования ф-ции:

1. Од-ть опред. ф-ции.

2. Чётность и нечётность ф-ии.

Если ф-ция нечётная, значит график ф-ции симметричен относительно начала координат. Если ф-ция чётная, значит график ф-ции симметричен относительно оси ОУ.

3. Периодичность

4. Точки разрыва

5. Найти критические точки 1-го рода.

6. Найти интервалы монотонности и экстремумы ф-ции.

7. Найти критические точки 2-го рода.

8. Найти интервалы выпуклости и точки перегиба.

9. Найти асимптоты графика ф-ии.

10. Найти точки пересечения графика с осями координат (если это возможно)

11. Построить график ф-ции.

2. Неопределённый .

Ф-ция F(x) назыв. первообразной для ф-ии f(x) в промежутке [a;b], если в любой точке этого промежутка её производная = f(x).

F’(x)=f(x)→d F(x)=f(x)dx, xэ[a,b]

Нахождение производной – это дифференцирование, а нахождение первообразной по заданной производной –интегрирование. Совокупность первообразных для ф-ции f(x) или для дифференциала f(x)dx назыв. неопределённым интегралом обозначается символом

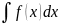
Таким образом

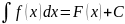
Если d[F(x)+C]=f(x)dx

Cвойства неопределённого интеграла:

1. Неопределённый интеграл от дифференциала ф-ции =этой ф-ии «+» произвольная постоянная

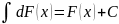
2. Неопределённый интеграл алгебраической сумме неопред-ных интегралов этих ф-ций

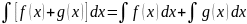
3. Дифференциал неопред. Интеграла = подынтегральному выражению, а производная интеграла = подынтегральной ф-ции. d (

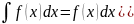
4. Постоянный множитель подынтегрального выражения можно выносить за знак неопределённого интеграла.

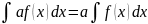
Методы интегрирования:

1. Метод непосредственного интегрирования

2. Метод подстановки

3. Метод интегрирования по частям

4. Метод интегрирования рациональных дробей.

3. Определённый интеграл.

Приращение F(b)-F(a) любой первообразной для ф-ции f(x) при изменении аргумента от х=b назыв. определённым интегралом от ф-ции f(x) и обозначается:

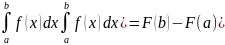
Ф-ция f(x) предполагается непрерывной на отрезке [a;b]. Значения a и b назыв. соответственно нижним и верхним пределами интеграла. Значения опред. интеграла зависит от вида ф-ции f(x) и от пределов интеграла. В отличии от неопред. Интеграла, который явл. ф-ей, в результате вычисления опред. интеграла получается число.

Свойства определённого интерграла:

1. При перестановке пределов интеграла знак интеграла меняется на противоположный

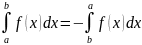
2. Опред. интеграл аглебраической суммы ф-ций =алгебраической сумме опред. интегралов этих ф-ций.

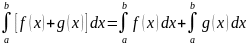
3. Постоянный множитель подынтегрального выражения можно выносить за знак определённого интеграла:

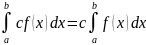
Правило вычисления определённого интеграла:

1. Вычислить неопр. Интеграл от той же ф-ции.

2. В полученную первообразную подставить вместо Х значения верхнего, а затем нижнего пределов интеграла.

3. Из результата подстановки верхнего предела вычесть результат подстановки нижнего предела.