6.1 Модели линейного программирования

Понятие линейности связано с понятиями пропорциональности и аддитивности (аддитивность - возможность суммирования результатов). Методами математического программирования решаются задачи на экстремум (максимум, минимум) функций многих переменных с ограничениями и на область изменения этих переменных. Из методов математического программирования наибольшее распространение получил метод линейного программирования. Слово программирование показывает, что они применяются для планирования, т.е. для составления плана (программы), который обеспечивал бы оптимальное использование материальных и трудовых ресурсов. Слово линейное определяет математическую природу этих моделей. Она состоит в том, что условия задач выражаются системой линейных уравнений или неравенств, содержащих неизвестные только первой степени. Для любых задач линейного программирования характерны три следующих условия (по академику В.С.Немчинову):

- наличие системы взаимосвязанных факторов;

- строгое определение критерия оценки оптимальности;

- точная формулировка условий, ограничивающих использование наличных ресурсов.

С учетом этих условий экономическим содержанием задач линейного программирования является отыскание наилучших способов использования имеющихся ресурсов, например, определение оптимального плана закрепления потребителей однородного груза за поставщиками.

Такого рода задачи получили название транспортных задач линейного программирования. Если нужно использовать разнородные ресурсы, например, различные машины, материалы и т.д. для выполнения какой-либо работы, то применяется общий метод линейного программирования, который получил в соответствии со своей математической основой название симплекс-метода, предложенного американским ученым Дж.Данцигом. Рассмотрим сущность модели линейного программирования на простейшем примере.

Пример. Пусть фирма специализируется на строительстве двух типов складских помещений. Известны производственные и ресурсные возможности фирмы, стоимость 1 кв.м каждого из складских помещений.

Требуется определить, сколько нужно строить складских помещений каждого типа, чтобы выручка от их продажи была максимальной (таблица 13).

Введем следующие обозначения:

х_j - количество изготавливаемых складских помещений j-oгo типа;

с_j - рыночная стоимость складского помещения;

а_ij - затраты i-oгo вида ресурсов на одно складское помещение j-oгo типа;

b_i - общий объем имеющихся ресурсов i-oгo вида.

Исходные данные, помещенные в таблице 13, представим в буквенном выражении (таблица 14).

Составим математическую модель. Показатель эффективности, который необходимо максимизировать, - выручка от реализации складских помещений (обозначим ее С), линейно зависит от элементов решения х₁ и х₂.

С = с₁х₁ + с₂х₂

(6.1)

Таблица 13 – Исходные данные к транспортной задаче линейного программирования

Наименование основных показателей	Типы складских помещений		Имеющиеся ресурсы
	I	II
1. Рыночная стоимость складского помещения (у.е.), С1, С2	100	200
2. Трудоемкость изготовления каркаса одного складского помещения, чел.-ч	ai1 67	ai2 168	bi 1600
3. Трудоемкость по изготовлению дверей, перегородок, полов на одно складское помещение, чел.-ч	8	8	140
4. Машиноемкость работ по подготовке фундамента	3.7	5.4	120
5. Машиноемкость монтажа каркаса складского помещения автомобиль-ным краном, маш.-ч	-	1.7	13
6. Трудоемкость по возведению оборудованию одного складского помещения, чел.-ч	125	100	2000

Таблица 14 – Исходные данные в буквенном выражении

Вид ресурса	Тип складского помещения
	I	II
b1	a11	a12
b2	a21	a22
b3	a31	a32
b4	a41	a42
b5	a51	a52

Запишем систему ограничений: (6.2)

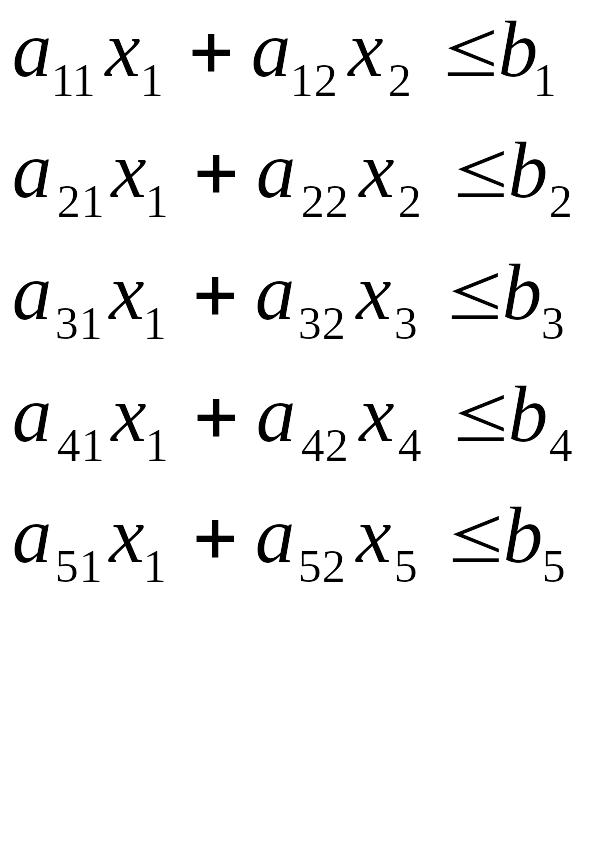
Эти линейные неравенства представляют собой ограничения, накладываемые на элементы решения х₁ и х₂.

Постановка задачи сводится к следующему: найти такие неотрицательные

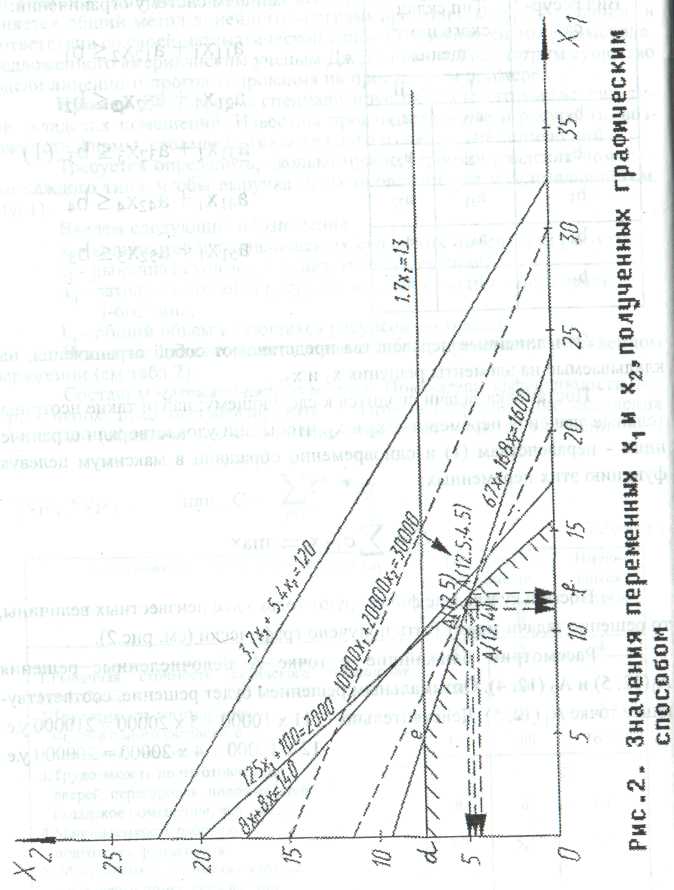
Рисунок 25 – Значения переменных Х₁ и Х₂, полученных графическим способом

значения переменных х₁ и х₂, чтобы они удовлетворяли ограничениям - неравенствам и одновременно обращали в максимум целевую функцию этих переменных:

(6.3)

Поскольку в задаче фигурируют только две неизвестных величины, то решение задачи может быть получено графически (рисунок 25).

Рассмотрим ближайшие к точке А целочисленные решения А₁ (12, 5) и А₂ (12, 4). Оптимальным решением будет решение, соответствующее точке А₁ (12, 5). Действительно,

11 x 10000 + 5 x 20000 = 210000 у.е.

12 x 10000 + 4 x 20000 = 200000 у.е.