4.4 Математическая модель эксперимента. Метод наименьших квадратов

После того как проведены первичная статистическая обработка результатов эксперимента и обоснование точности полученных экспериментальных данных необходимо найти аналитическую зависимость выходного параметра y от входных параметров (факторов) x₁, x₂, …, x_k.

Рассмотрим простейший случай. Пусть выходной параметр y зависит только от одного фактора x. В результате проведения эксперимента получим данные, представленные в таблице 3.

Таблица 3 – Результаты эксперимента

Параметры	Значения
x	x1	x2	…	xm
y	у1	y2	…	ym

Возникает задача найти функцию y = f(x), отражающую в основном характер экспериментальной зависимости, - это задача сглаживания экспериментальной зависимости. Так как y и x случайные величины, то кривая, проходящая через точки М_i (рисунок 10), не отражает основного характера зависимости y = f(x). Кривой, отражающей в основном характер экспериментальной зависимости у = f(х), будет кривая Г.

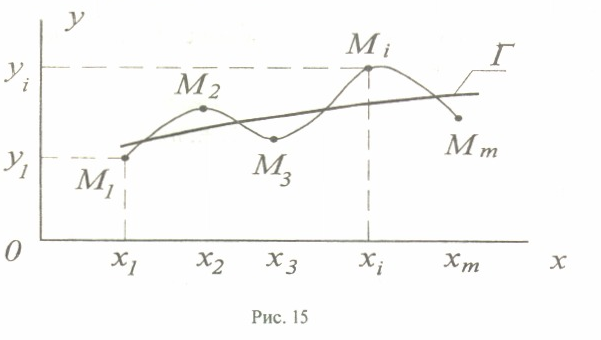
Рисунок 10 – Сглаживание экспериментальной зависимости

Решают две вспомогательные задачи.

1 Определение вида сглаживающей функции.

2 Определение значений параметров, входящих в сглаживающую функцию [17].

Первая задача решается исходя из дополнительной информации об эксперименте, вторая - математическими методами. Зачастую сглаживающая функция представляется в виде линейной комбинации неизвестных числовых параметров и некоторых известных линейно независимых функций

(4.14)

Такими функциями, например, могут быть

(4.15)

Для удобства дальнейших вычислений вводят в эту матрицу еще одну переменную, она называется «фиктивной» и во всех опытах равна x_0u = +1. В результате получена матрица размерностью N*(K+1). Вектор наблюдений образует другую матрицу, размерностью N*1.

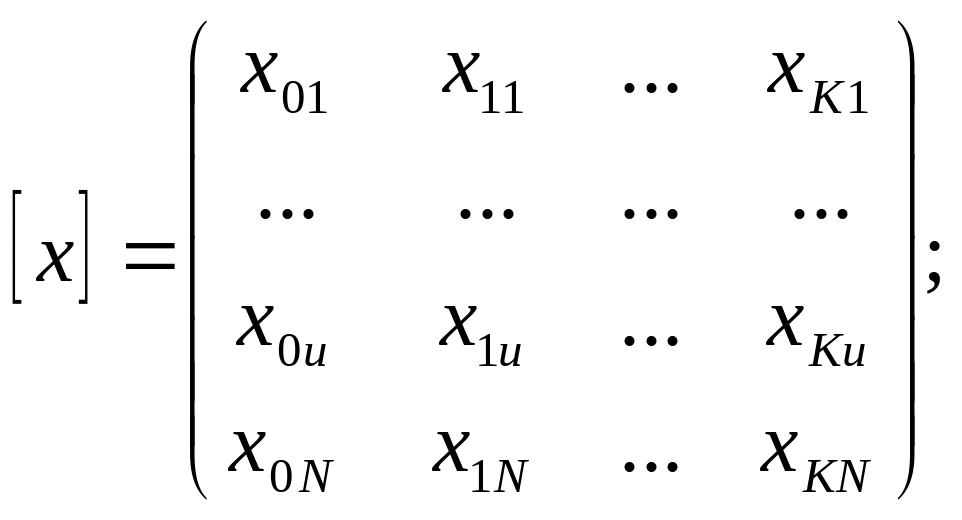
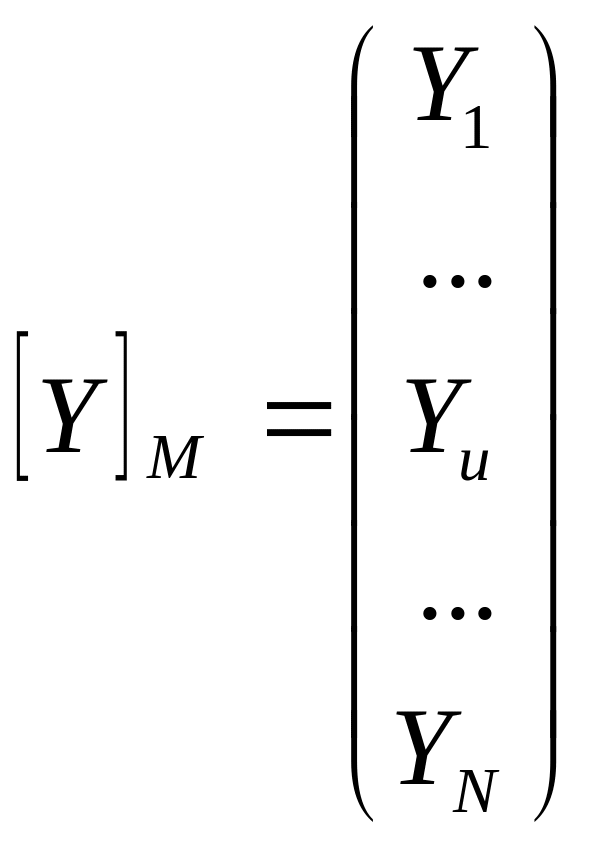. (4.16)

Рассмотрим на примере однофакторной модели идею метода наименьших квадратов, который дает наилучшие линейные оценки.

Для однофакторной модели (линейной) матрица содержит лишь два столбца. Необходимо подобрать такие значения b₀ и b₁ (или так провести прямую на графике (рисунок 11) в координатах X₁ и Y), чтобы модель наилучшим образом удовлетворяла данным. Провести прямую через все точки с координатами (X_1u и Y_u) практически невозможно. Это объясняется тем, что:

а) измерения Y_u точны, но гипотеза о линейном влиянии X₁ на Y не соответствует истине;

б) влияние X₁ на Y действительно линейно, но Y_u измерено со значительной среднеквадратической ошибкой S_э;

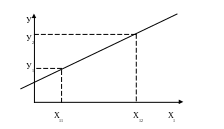
Рисунок 11 – Графическое изображение однофакторной модели

y=b₀x₀ + b₁x₁

в) одновременно несовершенна гипотеза линейности и существует ошибка измерения S_э.

Следовательно, всегда между наблюдаемыми значениями (Y_u) и расчетными значениями (Ŷ_u) возможна разница (∆u):

∆u =Y_u - Ŷ_u (4.17)

Необходимо свести общую разницу к минимуму. При этом наименее громоздкие вычисления получаются, если минимизировать не сумму абсолютных отклонений по всем опытам, , а сумму квадратов отклонений:

(4.18)

При подстановке значений Ŷ_u из модели для каждого опыта получим:

(4.19)

Для нахождения минимума функции необходимо приравнять к нулю частные производные по всем неизвестным, т.е. по b₀ и b₁. Получаем систему нормальных уравнений, при решении которых и будут вычислены неизвестные коэффициенты модели:

(4.20)

сокращая оба уравнения на «-2» и производя почленное суммирование, получим:

(4.21)

Далее вводим обозначения:

N(u)=(00) ΣX_1u=(01) ΣY=(0Y)

ΣX_1u=(10) ΣX_1u²=(11) ΣYX_1u=(1Y)

Тогда система уравнений примет вид:

(4.22)

Неизвестные оценки коэффициентов модели образуют вектор b:

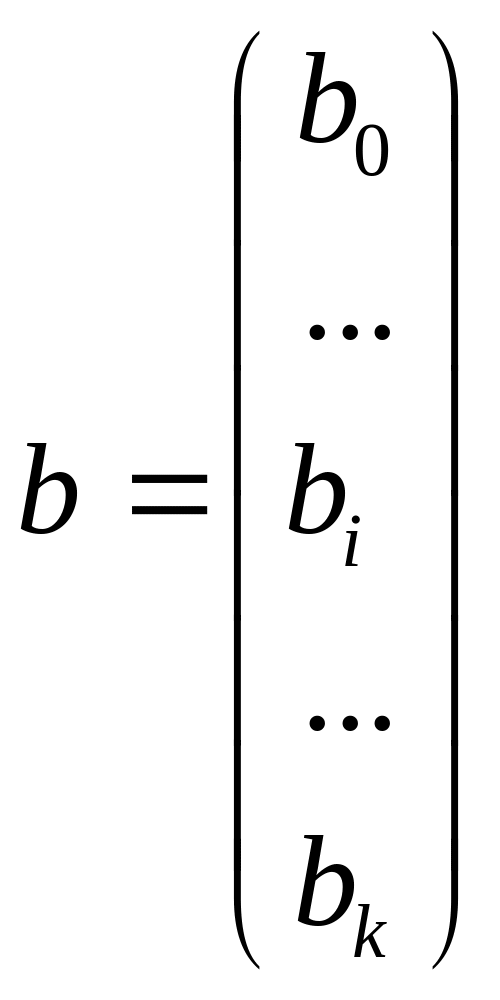(4.23)

Известные априори суммы (00), (i0), (ij) и (ii), определенные только уровнями факторов X_i в информационной таблице, образуют квадратичную матрицу М размером (k+1)*(k+1):

М= 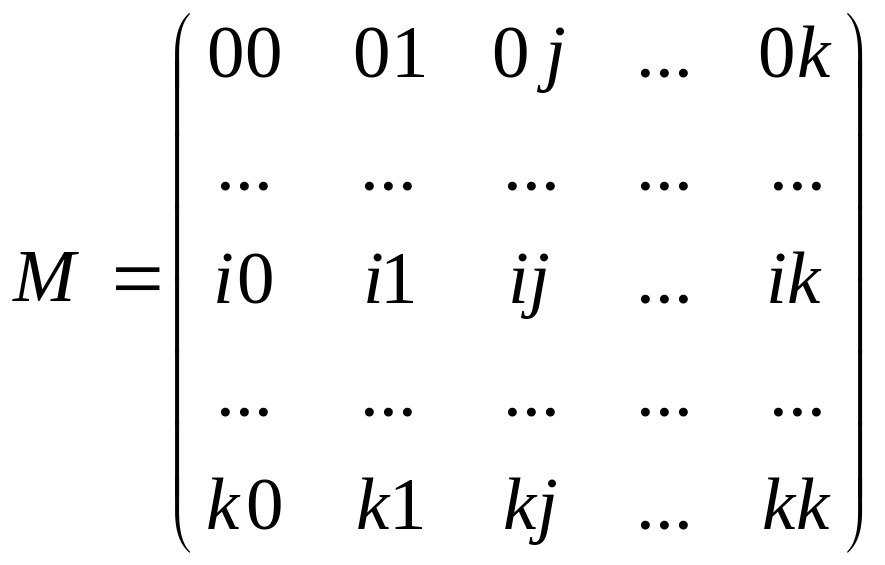(4.24)

Эта матрица называется матрицей моментов плана, ее можно получить из матрицы плана X₁, если последнюю умножить слева на транспонированную матрицу X^Т: М= X^Т* X.

С целью исследования свойств и обобщения результатов для матриц различных планов X матрицу М целесообразно нормировать по числу опытов, получая информационную матрицу M_N= .

Известные апостериори суммы (0Y) и (iY), включающие результаты эксперимента, образуют вектор Y_M, являющийся произведением X^Т на вектор наблюдений Y:

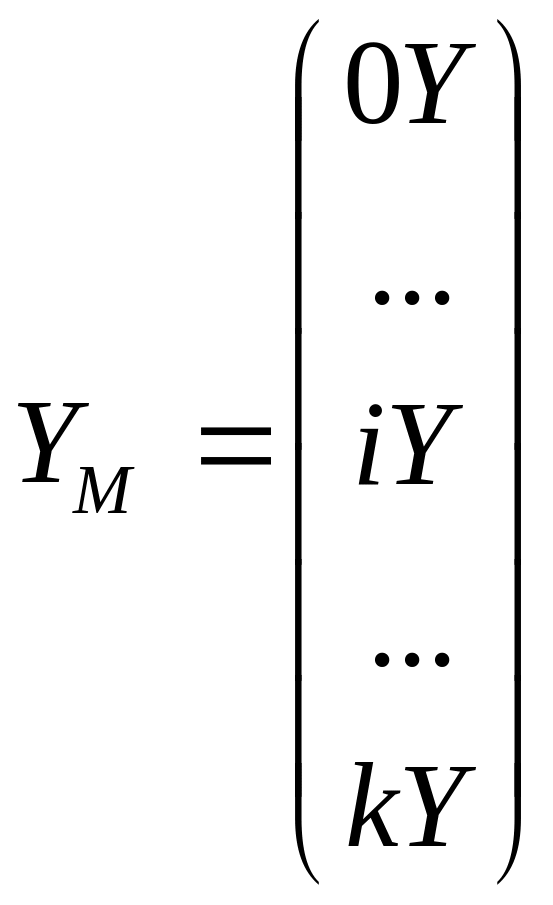Y_M=X^ТY (4.25)

Следовательно, в матричной форме система нормальных уравнений записывается:

Мb= У_М (4.26)

А с учетом матрицы Х: Х^ТХ^В= Х^ТУ из нее определяется вектор оценок коэффициентов:

b = М^-1У_М = ( )^-1Х^ТУ = N^-1M_N^-1X^TY = ДХ^ТY = LY (4.27)

В данном случае выделены две новые независимые от результатов эксперимента матрицы: так называемая D-матрица, или ковариационная, элементы которой оценивают статистические характеристики модели, и так называемая L-матрица, элементы которой позволяют рассчитывать оценки b_i без обращения матриц по простым формулам с помощью микрокалькуляторов.

Д = М^-1 = (Х^ТХ)^-1 (4.28)

L = DХ^Т = (Х^ТХ)^-1Х^Т (4.29)

Неизвестные оценки в системе нормальных уравнений можно рассчитать через определитель det M = A матрицы моментов и определителя det M_i = A_i матриц M_i, образуемых путем замены i-го столбца на вектор-столбец У_М:

b_i = det M_i/ det M = A_i/A (4.30)

Таким образом, для однофакторной модели при использовании правила Крамера используются простые формулы:

(4.31)

Ковариационная матрица D = Х^ТХ^-1 определяется только матрицей независимых переменных Х, т.е. планом эксперимента, поэтому априорный анализ ее свойств лежит в основе синтеза этих планов [7]. Точность оценивания параметров модели зависит от матрицы М или другими словами от выбора точек Х_ij . Это даёт возможность ставить задачу об оптимальном выборе точек, то есть планировании экспериамента. Набор координат этих точек называют планом эксперимента.

Рассмотрим пример. Найти функцию, отражающую экспериментальную зависимость у от x, используя данные таблицы 4.

Таблица 4 – Результаты эксперимента

Параметры	Значения параметров
x	1,20	1,31	1,40	1,61	1,74	1,80	2,00	2,14	2,19	2,41
y	0,54	0,59	0,67	0,76	0,85	0,97	1,07	1,18	1,27	1,30

Функцию у = f(х) возьмем в виде

y = C₁x² + C₂x + C₃.

Неизвестные С₁, С₂, С₃ определим из условий (4.15).

Здесь φ₁(х) = x², φ₂(х) = х, φ₃(х) = 1.

В результате получим систему

128,94С₁ + 64,30С₂ + 33,17С₃ = 34,63;

64,30 С₁ + 33,17 С₂ + 17,80С₃ = 17,60;

33,17 С₁ + 17,80 С₂ + 10,00С₃ = 9,29.

Решив эту систему, найдем С₁ = 0,168; С₂ = 0,102; С₃ = 0,189.

Следовательно, функциональная зависимость у от х имеет вид

у = 0,168х² + 0,102х + 0,189.