4.5 Получение некоторых эмпирических формул

В том случае, когда в сглаживающую функцию (4.14) искомые параметры входят нелинейно, вначале формулу нужно преобразовать таким образом, чтобы каждый параметр входил линейно, а потом найти его значение методом наименьших квадратов [20].

Пусть вид сглаживающей функции

y = e^ax (4.32)

Значения х и у даны в таблице 9. Прологарифмируем выражение (4.32) lny = ax. Получим новую функцию

ax (4.33)

где = ln y можно получить из таблицы 9. Параметр а находится из минимизации функции

(4.34)

Используя условие (4.15), найдем

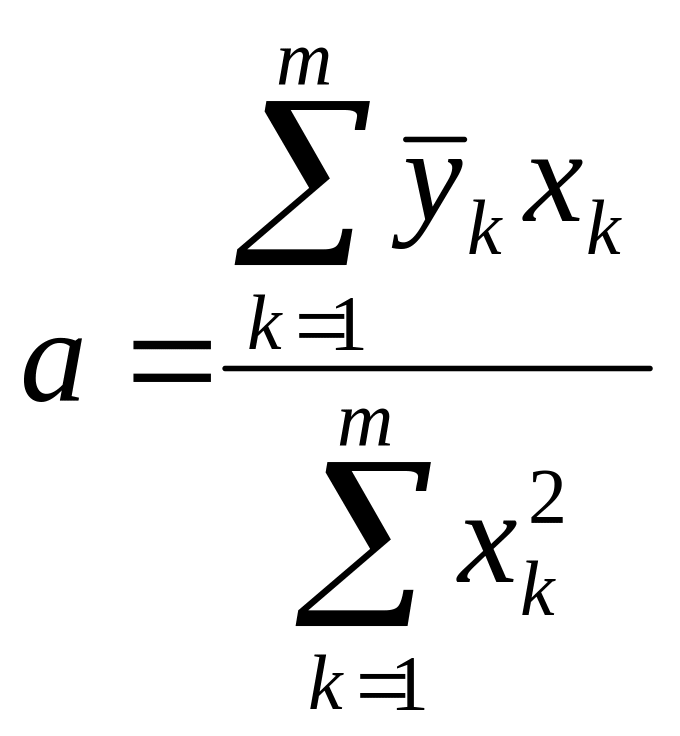(4.35)

Если сглаживающая функция имеет вид

y = a lnx (4.36)

то представим ее так: y = a где = ln x получим из таблицы 9. Параметр а находится из условия минимума функции

(4.37)

Так что

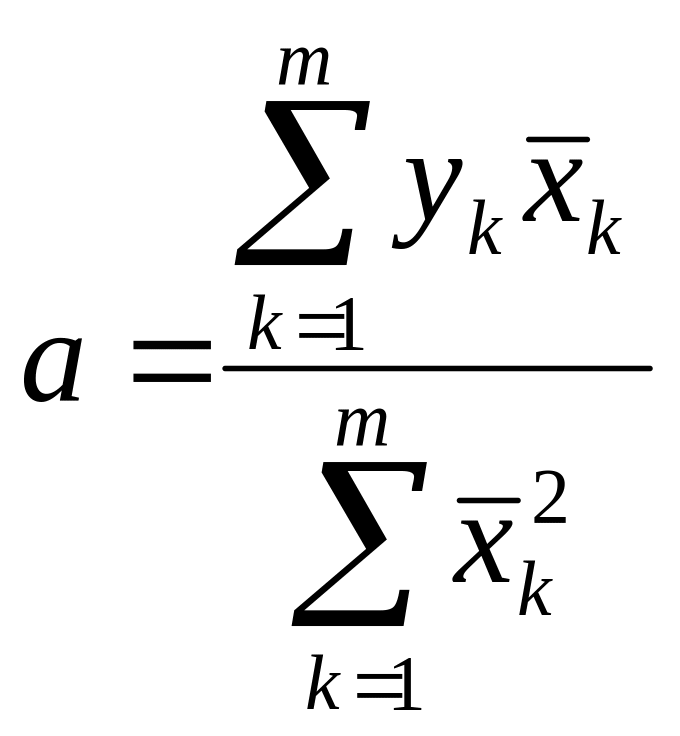(4.38)

4.6 Метод наименьших квадратов для функции нескольких переменных

Будем теперь считать, что исследуемая величина у связана некоторым образом с величинами х₁, х_2, …, х_k - входными величинами (факторами), значения каждого из которых могут быть выбраны произвольно из некоторой области.

Пусть связь у с х₁, х₂, ..., х_k характеризуется зависимостью (видом регрессии у на х₁, х₂, ..., х_k).

(4.39)

Функцию называют функцией отклика. Эта функция обычно неизвестна экспериментатору, но, обладая некоторой информацией или интуицией, экспериментатор выбирает вид этой функции. Будем брать эту функцию в виде линейно зависящей от нескольких числовых параметров θ₁, θ₂, …, θ_m.

(4.40)

Вид функции f_i - известен. Обозначим

(4.41)

В векторных обозначениях выражение (4.40) можно записать:

(4.42)

Чтобы получить математическую модель процесса, нужно определить вектор θ в (4.42) (оценить и оценки найти наилучшие в некотором смысле). Доказано, что наилучшие линейные оценки , полученные для , дает метод наименьших квадратов. В выражении (4.42) вектор входит как раз линейно. Есть и другие способы оценки . Заметим, что эти оценки должны быть состоятельными, несмещенными и обладать наименьшими дисперсиями среди всех оценок . Такие оценки и называются наилучшими линейными оценками.

Предположим, что в точках (n - разных наборов факторов факторного пространства были проведены независимые измерения y₁, y₂, …, y_n с дисперсиями σ²₁, σ²_{1, …,} σ²_n. В дальнейшем будем считать, что y₁ - это среднее выборочное значение, а среди нет одинаковых.

Нам нужно построить оценку параметров . Известно, что наилучшая линейная оценка минимизирует сумму взвешенных квадратичных отклонений.

(4.43)

где .

Условия минимума для (4.43) имеют вид

. (4.44)

Откуда, решив систему линейных алгебраических уравнений (4.44), найдем - оценки для θ₁, θ₂, …, θ_m. Подставляя эти значения в (4.42), найдем аналитическую зависимость у от х₁, х₂, ..., x_k, т. е. математическую модель исследуемого экспериментально процесса.

4.7 Дисперсионная матрица оценок

Распишем систему уравнений (4.44) подробнее:

(4.45)

где j = 1, 2, …, m.

Эту систему после преобразования запишем в виде

(4.46)

где j = 1, 2, …, m.

Пусть (4.47)

Тогда

(4.48)

Обозначим

(4.49)

Так что

(4.50)

Теперь соотношение (4.46) можно записать в виде

(4.51)

А всю систему запишем так:

(4.52)

Решение этой системы в матричной форме имеет вид

(4.53)

где J - информационная матрица Фишера.

(4.54)

Обратная матрица является дисперсионной матрицей оценок

(4.55)

Дисперсионная матрица играет большую роль при выборе наилучших оценок. Оценка предпочтительнее оценки , если дисперсионная матрица меньше дисперсионной матрицы или определитель

(4.56)

Итак, наилучшие линейные оценки для рассматриваемого эксперимента найдены. Но может быть и другой эксперимент с другим n и другим набором факторов. Следует обратить внимание на то, что наилучшей линейной оценкой поверхности отклика является

(4.57)

Дисперсия оценки равна .