
- •Теорія ймовірності та математична статистика історія виникнення та розвитку теорії ймовірностей
- •Основні поняття теорії ймовірностей
- •Перестановки, розміщення, комбінації
- •Геометрична ймовірність
- •Сума і добуток подій
- •Теорема додавання ймовірностей
- •Теорема множення ймовірностей
- •Теорема додавання сумісних подій
- •Формула повної ймовірності
- •Формула Байєса
- •Послідовності незалежних випробувань
- •Локальна теорема лапласа
- •Інтегральна теорема Лапласа
- •Формула Пуассона (теорема Пуассона)
- •Випадкова величина
- •Закон розподілу ймовірностей дискретної випадкової величини
- •Функція розподілу випадкової величини
- •Властивості функції розподілу:
- •Щільність розподілу випадкової величини
- •Властивості функції щільності розподілу:
- •Числові характеристики випадкової величини
- •Властивості математичного сподівання:
- •Властивості дисперсії:
- •Розподіл Пуассона
- •Рівномірний розподіл
- •Нормальний розподіл
- •Система випадкових величин
- •Функція розподілу двох випадкових величин
- •Властивості функції розподілу:
- •Щільність розподілу системи двох випадкових величин
- •Залежні і незалежні випадкові величини
- •Числові характеристики системи двох випадкових величин
Формула Байєса
До сих пір ми розглядали ймовірність подій до проведення дослідів, тобто в комплексі умов не враховувався результат проведеного досліду. Поставимо тепер таку задачу: маємо повну групу несумісних гіпотез Н1, Н2, ..., Нn. Відомі ймовірності гіпотез Р(Н1), Р(Н2), ..., Р(Нn) в результаті досліду відбулася подія А. Відомі умовні ймовірності Р(А/Н1), Р(А/Н2), ..., Р(А/Нn).
Виникає питання, яким чином зміняться ймовірності гіпотез у зв’язку з появою події А, тобто треба знайти умовні ймовірності Р(Н1/А), Р(Н2/А), ..., Р(Нn/А).
З теореми множення ймовірностей маємо Р(АНі)=Р(А)Р(Ні/А)=Р(Ні)Р(А/Ні).
Звідси, Р(Н1/А)=![]() ,
,
або
|
Р(Ні/А)= – ця формула називається формулою Байєса |
Задача. Прилад може бути зібраний з високоякісних деталей або зі звичайних. 40% приладів зібрані з високоякісних деталей. Надійність приладу з високоякісних деталей 0,95, зі звичайних 0,7. прилад протягом часу t працював безвідмовно. Знайти ймовірність того, що:
1) прилад виготовлений з високоякісних деталей;
2) прилад виготовлений зі звичайних деталей.
Розв’язання. Гіпотези: Н1 – прилад виготовлений з високоякісних деталей,
Н2 – прилад виготовлений зі звичайних деталей.
Р(Н1)=0,4 (40%); Р(Н2)=0,6 (60%).
Відбулася подія А – прилад безвідмовно працював протягом часу t. Ймовірність того, що прилад з високоякісних деталей буде працювати невідмовно, іншими словами надійність приладу, дорівнює Р(А/Н1)=0,96. Надійність приладу зі звичайних деталей Р(А/Н2)=0,7.
За формулою Байєса знаходимо
ймовірність того, що прилад був
виготовлений з високоякісних деталей
Р(Н1/А)=![]() =
=![]() ==0,475.
==0,475.
Аналогічно, знаходимо
ймовірність того, що прилад виготовлений
зі звичайних деталей Р(Н2/А)=![]() =0,525.
=0,525.
Послідовності незалежних випробувань
І. Нехай неодноразово повторюється деякий дослід при однакових умовах. В результаті кожного досліду подія А може відбутися або не відбутися.
Нас цікавить ймовірність загального числа появи події А в серії дослідів. Наприклад, команда волейболістів провела 10 ігор. Яка ймовірність того, що вона виграла 6 ігор.
Будемо розглядати незалежні випробування, тобто такі, що ймовірність результату кожного випробування не залежить від результатів інших випробувань.
Отже, проведено n незалежних випробувань. В кожному випробуванні подія А може відбутися або не відбутися. Ймовірність появи події А в одному досліді дорівнює р. Ця ймовірність однакова в кожному досліді. Ймовірність того, що подія А не відбудеться дорівнює q (q=1-р). Треба знайти ймовірність Рm,n того, що в n випробуваннях подія А настане (відбудеться) m раз.
Позначимо через: Вm,n
подію, яка полягає в тому, що подія А
відбудеться m
раз в n дослідах;
Аі
– поява події А
в і-тому
досліді,
![]() – неповна подія А
в і-тому
досліді.
– неповна подія А
в і-тому
досліді.
Запишемо подію Вm,n у вигляді суми добутків подій Аі і .
Вm,n=А1А2...
Аm![]() ...
...![]() +...+
+...+![]()
Число доданків тут дорівнює числу комбінацій з n елементів. Доданки є несумісними подіями. Ймовірність суми несумісних подій дорівнює сумі ймовірностей цих подій. Крім того випробування незалежні. Тому ймовірність подій Вm,n можна записати так:
Р(Вm,n)=рmqn-m+…+pmqn-m; Р(Вm,n)=![]() ;
Р(Вm,n)=
;
Р(Вm,n)=![]() ;
;
|
Рm,n= – ця формула називається формулою Бернуллі. |
Ймовірність Рm,n дорівнює коефіцієнтові при хm в розкладанні бінома (q+px)n за степенями х, тому ймовірності Рm,n (m=1, 2, ..., n) називаються біноміальним розподілом ймовірностей.
Приклад. Що є більш ймовірним, виграти у рівносильного гравця 3 партії з 4, чи 5 з 8.
Розв’язання.
Дослід – одна партія із супротивником.
Подія А –
виграш у супротивника. Оскільки гравці
рівносильні, то ймовірність виграшу
однієї партії дорівнює
![]() .
.
Р3,4=![]()
Р5,8=![]()
Отже, Р3,4> Р5,8
Очевидно, що Р0,n+Р1,n+…+Pn,n=1.
II. Тепер розглянемо такий випадок, коли ймовірність появи події А змінюється при проведенні n випробовувань.
Отже, нехай проводимо n випробувань. Ймовірність появи події А в і-тому випробуванні дорівнює рі, не появи – qi=1-pi.
Знайти ймовірність появи події А m раз в n випробовуваннях Рm,n.
Ймовірність Рm,n дорівнює коефіцієнтові при хm в добутку (q1+p1x)(q2+p2x)…(qn+pnx).
Задача. Чотири стрільці роблять по одному пострілові в мішень. Ймовірність влучення в мішень для 1-го стрільця р1=0,8; для 2-го стрільця р2=0,7; для 3-го стрільця р3=0,6; для 4-го стрільця р4=0,5. Знайти ймовірність того, що
1) в мішень не влучить жоден стрілець;
2)влучить тільки один стрілець;
3) влучать два стрільці;
4) влучать тільки три стрільця;
5)влучать усі стрільці;
6) влучить хоча б один стрілець;
7) влучать не менше ніж два стрільця.
Розв’язання. Оскільки ймовірність влучення для стрільців різні, то скористаємось останньою формулою при q1=1-0,8=0,2; q2=0,3; q3=0,4; q5=0,5.
(0,2+0,8х)(0,3+0,7х)(0,4+0,6х)(0,5+0,5х)=0,012+0,106х+
0,32х2++0,394х3+0,168х4.
Відповідь: 1) Ймовірність того, що в мішень не влучить жоден стрілець Р0,4=0,012.
2) Ймовірність того, що влучить тільки один стрілець Р1,4=0,106.
3) Р2,4=0,32.
4) Р3,4=0,394.
5) Р4,4=0,168.
6) Р1,4+ Р2,4+ Р3,4+ Р4,4=0988=1- Р0,4=1-0,012=0,988.
7) Р2,4+ Р3,4+ Р4,4=1-Р0,4-Р1,4=0,882.

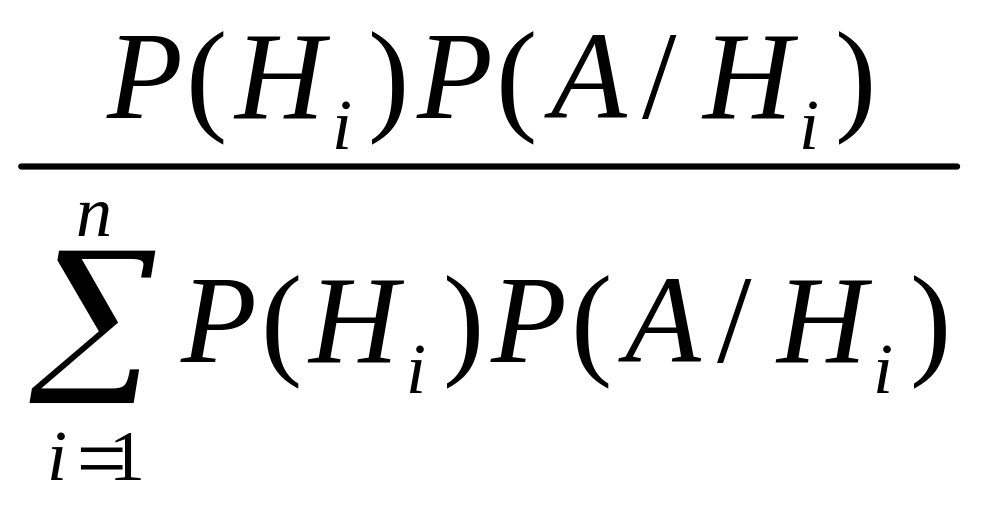 ,
(і=1,2,...,n)
,
(і=1,2,...,n)