Перестановки, розміщення, комбінації

Для обчислення числа n і m в формулі часто користуються поняттями комбінаторики.

Перестановками з n елементів називаються упорядковані сукупності цих елементів.

Число перестановок з n елементів обчислюється за формулою:

Qn=n!

(n= )

З трьох елементів а, в, с можна скласти Q₃= = = перестановок. Запишем їх (а, b, с); (а, с, b); (с, b, а); (с, a, b);

(b, с, а); (b, а, с).

Задача В урні 5 занумерованих куль. З урни навмання беруть кульку за кулькою.

Знайти ймовірність того, що номери кульок підуть у порядку зростання.

Розв’язання. А – номери куль ідуть у порядку зростання.

Загальна кількість випадків дорівнює числу перестановок з 5 елементів

n=Q₅=5!= =120.

Число сприятливих випадків m=1 (номери йдуть у порядку зростання).

Отже, Р(А)= .

Розміщеннями без повторень з n елементів по m називають сукупності по m елементів які відрізняються одна від одної або складом елементів, або їх порядком.

Число розміщень без повторень з n елементів по m обчислюється за формулою:

R =

З трьох елементів а, в, с можна скласти R = = = розміщень.

Запишем їх (а, b); (а, с); (b, с); (b, а); (с, а); (с, b).

Задача. На столі лежали цифри 1, 2, 3, 4, 5, 6, 7, 8, 9, 0 на розрізних картках. Дитина взяла дві картки з цифрами і поклала поряд. Знайдіть ймовірність того, що дитина склала число 25.

Розв’язання. А – дитина склала число 25. Загальна кількість випадків складання числа з двох карток дорівнює R = = = = .

Сприятливий для події А лише один випадок (25).

Отже, Р(А)= .

Комбінаціями з n елементів по m елементів називаються сукупності з m елементів, які відрізняються одна від одної хоча б одним елементом.

Число комбінацій з n елементів по m елементів обчислюється за формулою:

C =

З трьох елементів а, b, с по два елемента можна скласти C = = = комбінації. Запишемо ці комбінації (а, b); (а, с); (b, с).

Задача. В партії з 20 деталей 6 бракованих. З партії навмання беруть 5 деталей. Знайти ймовірність того, що серед взятих п’яти деталей будуть 2 браковані.

Розв’язання. 5 деталей з 20 можна взяти С способами С = =

= =

= = .

2 браковані деталі з 6 можна взяти С способами

С = = = _.

Серед 5 взятих деталей 3 стандартні. Три стандартні деталі з 14 можна взяти C способами. C = = _.

Всього способів взяття 3 стандартних деталей і 2 бракованих дорівнює С C . Ймовірність того, що серед взятих п’яти деталей будуть 2 браковані обчислимо за формулою .

= = _{= .}

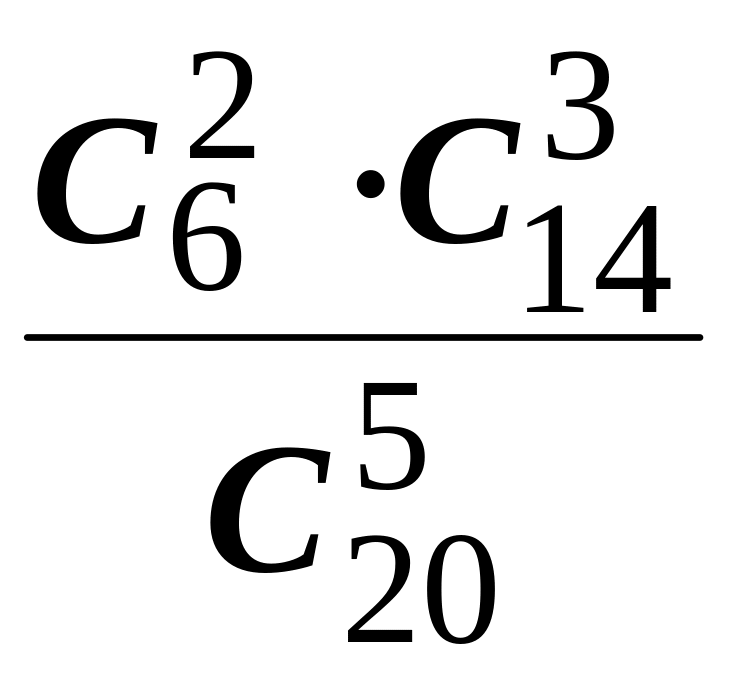Геометрична ймовірність

Н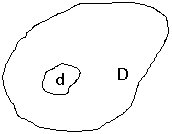 а практиці часто зустрічаються досліди, які мають нескінчену кількість результатів. В таких випадках формулу Р(А)= не можна використовувати. Тоді використовують метод геометричної ймовірності.

Розглянемо його для двомірного простору. Нехай на площині маємо деяку область D, площа якої дорівнює S_D. В області D міститься друга область d з площею S_D. В область D навмання кидається точка. Обчислити ймовірність того, що точка влучить в область d. Кинута точка може попасти в довільну точку області D, ймовірність попадання в яку-небудь частину області D пропорційна площі цієї частини, і не залежать від її розміщення і форми. Отже, ймовірність попадання в область d при киданні навмання точки в область D дорівнює:

В випадках одномірної і трьохмірної області D замість площі треба брати відповідно довжину і об’єм.

Поняття геометричної ймовірності можна використовуватися для розв’язку деяких задач теорії ймовірностей.

Задача 1. Задача про зустріч. Дві особи А і В домовилися зустрітись в певному місці. Причому кожен з них приходить туди незалежно від іншого у випадковий момент між 13 і 14 годинами дня. Той, хто приходить першим, чекає 20 хв., і якщо другий за цей час не прийде, перший залишає місце зустрічі. Знайти ймовірність того, що зустріч відбудеться

Розв’язання. Позначимо моменти приходу осіб А і В в місце зустрічі через х та у, тоді простір елементарних подій  можна зобразити як одиничний квадрат у системі координат хОу

={(х, у) | (х, у) R², 0x1, 0y1}.

Згідно з умовою, зустріч відбудеться якщо різниця між моментами приходу не перевищує 20 хв= год, тобто

або, якщо розкрити модуль, то х- £y£х+ .

Отже, зустріч відбудеться в точках де виконуються умови К={(х, у) | (х, у) R², 0x,у1, х- £y£х+ }.

y 1  В К 0 А 1 С x	Ймовірність зустрічі згідно означення геометричної ймовірності дорівнює. Р(А)= Очевидно, що S()=1, S(K)=1-2SABC=1-2 = = , отже Р(А)= .

Задача 2. Задача Бюрфона. На горизонтальній площині проведено паралельні прямі, які розташовані одна від одної на відстані 2а. На площину випадково кидається тонка голка довжиною 2l (la). Знайти ймовірність того, що голка перетне яку-небудь пряму.

Розв’язання. Для характеристики положення голки на площині введемо два числа: х – відстань від середини голки до найближчої прямої (0xа),  – кут нахилу до напрямку прямих (0).

В С 2a l  А Д

В прямокутній системі координат (, х) повний простір елементарних подій буде прямокутником  ={(, х) | (, х,) R2, 0, 0£х£а}.

Щоб голка перетнула одну із прямих потрібно щоб відстань х не перевищувала довжину відрізка СD, тобто

або

.

Така нерівність виділяє з прямокутника  область К, що лежить під синусоїдою.

x a  l K 0 /2  

Тоді Р(А)=

Очевидно S()=a.

S(K)=l

Тоді Р(А)=

Ця задача цікава тим, що дає змогу обчислити число  експериментально. Дійсно, якщо кинути голку n разів із них вона m разів перетне одну із прямих, то Р(А) Тоді з наближеної рівності

Маємо

Ця формула може використовуватись для експериментального обчислення числа , наприклад при 5000 киданнях (n=5000) 3,159