
- •Теорія ймовірності та математична статистика історія виникнення та розвитку теорії ймовірностей
- •Основні поняття теорії ймовірностей
- •Перестановки, розміщення, комбінації
- •Геометрична ймовірність
- •Сума і добуток подій
- •Теорема додавання ймовірностей
- •Теорема множення ймовірностей
- •Теорема додавання сумісних подій
- •Формула повної ймовірності
- •Формула Байєса
- •Послідовності незалежних випробувань
- •Локальна теорема лапласа
- •Інтегральна теорема Лапласа
- •Формула Пуассона (теорема Пуассона)
- •Випадкова величина
- •Закон розподілу ймовірностей дискретної випадкової величини
- •Функція розподілу випадкової величини
- •Властивості функції розподілу:
- •Щільність розподілу випадкової величини
- •Властивості функції щільності розподілу:
- •Числові характеристики випадкової величини
- •Властивості математичного сподівання:
- •Властивості дисперсії:
- •Розподіл Пуассона
- •Рівномірний розподіл
- •Нормальний розподіл
- •Система випадкових величин
- •Функція розподілу двох випадкових величин
- •Властивості функції розподілу:
- •Щільність розподілу системи двох випадкових величин
- •Залежні і незалежні випадкові величини
- •Числові характеристики системи двох випадкових величин
Рівномірний розподіл
Неперервна випадкова величина має рівномірний розподіл на відрізку [a, b], якщо на цьому відрізку щільність розподілу випадкової величини стала, а поза ним дорівнює нулю
f(x)=![]() де
С –
const.
де
С –
const.
Оскільки площа, що обмежена
прямими: х=а;
х=b; y=0;
y=C
дорівнює ймовірності попадання на
відрізок [a, b]
і значить дорівнює 1, то (b-a)C=1,
C=![]() .
.
Отже, f(x)=![]()
Знайдемо функцію рівномірного розподілу F(x).
При ха F(x)=![]() =0;
=0;
При a<xb F(x)=![]() ;
;
При x>b F(x)=![]() .
.
О тже,
F(x)=
тже,
F(x)=![]() f(x)
f(x)
1
x
0 a mx b
Визначимо математичне сподівання дисперсії і середнє квадратичне відхилення величини Х, що має рівномірний розподіл.
mx=![]()
Dx=![]() .
.
σх=![]() .
.
Нормальний розподіл
Нормальний закон розподілу (закон Гауса) часто зустрічається на практиці. Щільність ймовірності нормального розподілу має такий вигляд:
f(x)=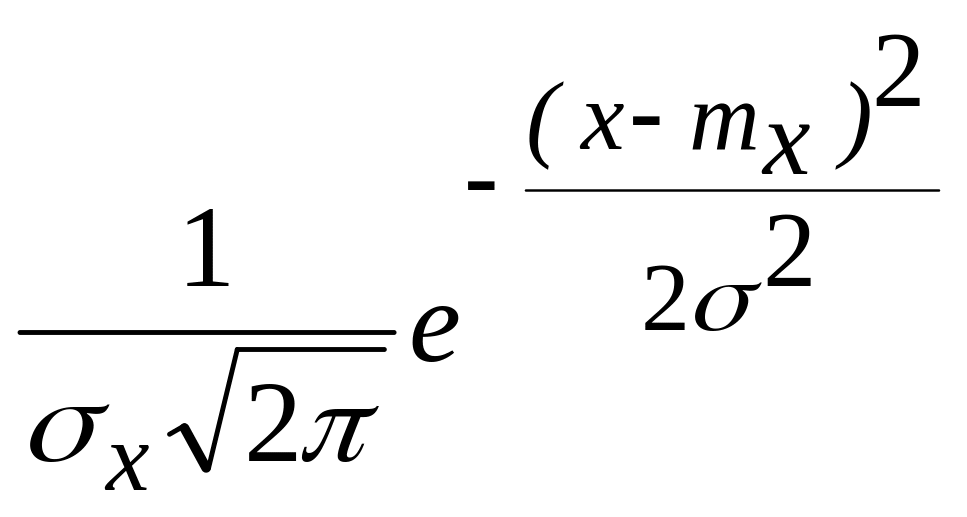 ,
де mx
і σх
– параметри нормального розподілу.
,
де mx
і σх
– параметри нормального розподілу.
Запишемо основні числові характеристики випадкової величини Х, що має нормальний розподіл ймовірностей.
Математичне сподівання M[X] дорівнює параметру mx, що входять в функцію f(x). M[X]=mx.
Дисперсія D[X] дорівнює параметру σх2. Середнє квадратичне відхилення дорівнює σх. Ймовірність попадання в заданий інтервал [, ) обчислюється за формулою:
Р(Х<)=![]() ,
,
де (х) - функція Лапласа.
Задача. Помилка радіодалекоміра має нормальний закон розподілу ймовірностей. Математичне сподівання цієї помилки 5 м, а середнє квадратичне відхилення дорівнює 10 м. Знайти ймовірність того, що виміряне значення дальності буде відрізнятися від істинного не більше ніж на 20 м.
Розв’язання. mx=5; σх=10.
Р(-20Х<20)=![]() =(1,5)-(-2,5)=
=(1,5)-(-2,5)=
=0,4332+0,4938=0,9270
Система випадкових величин
На практиці часто зустрічаються задачі, в яких результат досліду описується не однією випадковою величиною, а двома, трьома і т. д. випадковими величинами.
Наприклад, точка попадання при вистрелі може бути визначена двома координатами.
С истему
двох випадкових y
величин геометрично D
истему
двох випадкових y
величин геометрично D
зображатимемо точкою або y (x,y)
вектором на площині.
Систему трьох
випадкових величин
зображатимемо точкою або 0 x x
вектором трьохмірного простору і т. д.
При вивченні систем випадкових величин ми розглянемо систему двох випадкових величин. Всі результати можна розповсюдити на систему з довільною кількістю випадкових величин.
Функція розподілу двох випадкових величин
Систему двох випадкових величин позначимо (Х, Y).
Функцією розподілу F(x, y) двох випадкових величин називають ймовірність того, що випадкова величина Х буде менше ніж х і випадкова величина Y буде менше ніж y.
F(x, y)=P(X<x, Y<y)
y
 (х,y) З
геометричної точки зору функція розподілу
F(x, y) є
ймовірність попадання випадкової точки
(Х, Y) в
нескінченний квадрант з вершиною в
точці (х, y).
(х,y) З
геометричної точки зору функція розподілу
F(x, y) є
ймовірність попадання випадкової точки
(Х, Y) в
нескінченний квадрант з вершиною в
точці (х, y).
0 x
Властивості функції розподілу:
1) функція розподілу F(x, y) неспадна відносно обох аргументів тобто,
при x2>x1 F(x2, y)F(x1, y);
при y2>y1 F(x, y2)F(x,y1).
Дійсно, якщо точку (x, y) здвинути правіше і вище, то ймовірність влучення в квадрат не зменшиться
2) F(-, x)=0; F(-, y)=0; F(-¥, -¥)=0.
3) F(x, ¥)=F1(x)=P(X<x); F(¥, y)=F2(y)=P(Y<y).
4) F(-¥,¥)=1, так як це ймовірність попадання випадкової величини на всю площину хОу.
5) Ймовірність попадання випадкової точки в прямокутник R, що обмежений прямими х=; х=; у=; у= виражається через функцію розподілу ймовірностей так:
Р((Х, Y)R)=F(, )-F(, )-F(,)+F(, ).
Це співвідношення легко перевірити користуючись геометричним змістом функції розподілу F(x, y)
 у
у
x
0
