2.4.3. Чисельні характеристики двовимірної випадкової величини. Коваріація і коефіцієнт кореляції

Чисельні характеристики складових і дво­вимірної випадкової величини ( ) визначають за формулами, які є аналогами для одновимірної випадкової величини. Специфічні властивості деяких чисельних характеристик двовимірної випадкової величини пов’язані зі залежністю її компонент.

А. В и п а д о к д и с к р е т н о ї в и п а д к о в о ї в е л и ч и н и. Основні чисельні характеристики складових для дискретної двовимірної випадкової величини ( ) виражаються формулами:

• математичні сподівання:

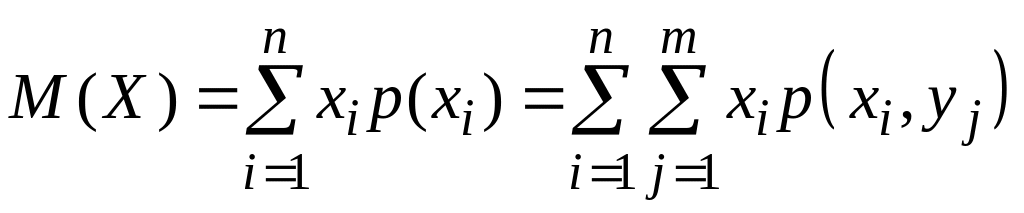, (2.61)

(2.61)

• дисперсії:

= (2.62)

= (2.62)

або

(2.63)

(2.63)

• середні квадратичні відхилення:

(2.64)

(2.64)

Приклад 2.33. Закон розподілу двовимірної дискретної випадкової величини (X, Y) задано таблицею:

X = xі Y = yj	–2	4	6
3 5			1,9a

Визначити число а і обчислити чисельні характеристики

Розв’язання. З умови (2.47) маємо, що

Із знайденим числом і доповненими ймовірностями і таблиця набу­ває такого змісту:

X = xі Y = yj	–2	4	6	p(yj)
3	0,17	0,22	0,21	0,6
5	0,03	0,18	0,19	0,4
p(xі)	0,2	0,4	0,4

За формулами (2.61), (2.61), (2.63), (2.63), (2.64), (2.64) обчислюємо чисельні характеристики:

;

;

Б. В и п а д о к н е п е р е р в н о ї в и п а д к о в о ї в е л и ч и н и. Основні чисельні характеристики для неперервної двовимірної випадкової величини (Х, Y) виражаються формулами:

• математичні сподівання:

(2.65)

(2.65)

де – густина розподілу складової Х, – густина розподілу складової Y.

Нагадаємо, що інтеграл за змінною у обчислюємо за умови, що х – стала величина, а інтеграл за змінною х – за умови, що у – стала величина;

• дисперсії:

(2.66)

(2.66)

або

(2.67)

(2.67)

• середні квадратичні відхилення:

(2.68)

. (2.68)

Якщо всі значення двовимірної неперервної випадкової величини містяться в прямокутнику , то в усіх наведених формулах замінюємо на .

Приклад 2.34. Двовимірна неперервна випадкова величина (X, Y) задана густиною:

де Обчислити чисельні характеристики М(Х), D(X), (X), М(Y), D(Y), (Y).

Розв’язання. Чисельні характеристики обчислюємо за формулами (2.65), (2.65), (2.67), (2.67), (2.68), (2.68):

;

;

;

;

; .

Важливими чисельними характеристиками двовимірної випадкової величини (Х, Y) є коваріація (або кореляційний момент) і коефіцієнт кореляції, які певною мірою відіграють роль показників взаємозв’язку між компонентами Х і Y.

Означення. Коваріацією (кореляційним моментом) двовимірної випадкової величини (Х, Y) називається математичне сподівання добутку відхилень складових цієї величини від їх математичних сподівань:

. (2.69)

Використовуючи означення математичного сподівання, одержимо:

• для дискретного розподілу

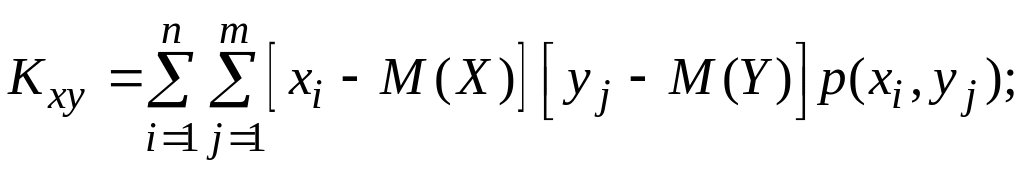(2.70)

• для неперервного розподілу

(2.70)

Коваріацію часто зручно виражати співвідношенням:

, (2.71)

яке у випадках дискретного і неперервного розподілів набуває вигляду:

, (2.72)

. (2.72)

Формулу (2.71) отримуємо зі співвідношення (2.69) безпосередніми обчисленнями з врахуванням властивостей математичного сподівання:

.

Для незалежних випадкових величин коваріація дорівнює нулю. Дане твердження є простим наслідком співвідношення (2.71), бо математичне сподівання добутку двох незалежних випадкових величин дорівнює добуткові математичних сподівань цих величин.

Коваріація двох випадкових величин (Х, Y) характеризує не тільки ступінь залежності випадкових величин, а й також їх розсіювання навколо точки [М(Х), М(Y)] на площині.

Вимірність коваріації дорівнює добуткові вимірностей випадкових величин Х і Y. Для того, щоб отримати безвимірну величину, до того ж таку, яка характеризує тільки залежність між випадковими величинами, а не їх розсіювання, вводиться поняття коефіцієнта кореляції.

Означення. Коефіцієнтом кореляції двовимірної випадкової величини ( ) називається відношення коваріації до добутку середніх квадратичних відхилень і цих величин:

(2.73)

Отже, величина характеризує ступінь залежності випадкових величин Х і Y, до того ж не будь-якої залежності, а тільки лінійної, яка проявляється в тому, що зі зростанням однієї випадкової величини друга має тенденцію також зростати або спадати: у першому випадку > 0 і кажуть, що випадкові величини Х і Y пов’язані додатною кореляційною залежністю; у другому – < 0 і кажуть, що випадкові величини пов’язані від’ємною кореляційною залежністю.

Покажемо, що для будь-яких двох випадкових величин Х і Y:

. (2.74)

Розглянемо допоміжну випадкову величину і обчислимо її дисперсію

.

Оскільки , то

.

Аналогічно, розглянувши випадкову величину і обчисливши її дисперсію, маємо нерівність:

.

Об’єднаємо дві одержані нерівності для і одержимо, що

.

Далі ділимо цю подвійну нерівність на добуток і маємо, що

.

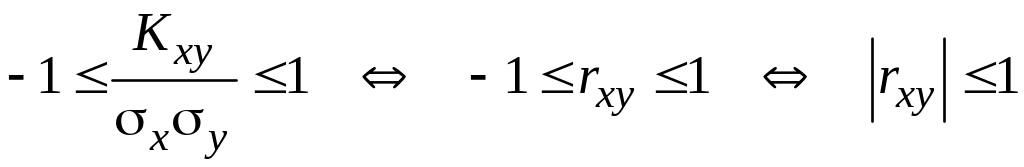Модуль коефіцієнта кореляції випадкових величин Х і Y характеризує ступінь тісноти лінійної залежності між ними. Якщо лінійної залежності немає, то = 0. Якщо між випадковими величинами існує функціональна лінійна залежність:

Y = aX + b,

то = +1 при а > 0 і = –1 при а < 0.

Означення. Дві випадкові величини Х і Y називаються корельованими, якщо коваріація (або коефіцієнт кореляції ), і некорельо­ваними, якщо коваріація (або коефіцієнт кореляції ).

Легко переконатися, що дві корельовані випадкові величини є також залежні. Обернене твердження правильне не завжди, тобто якщо дві випадкові величини залежні, то вони можуть бути як корельованими, так і некорельованими.

Приклад 2.35. Для двовимірної випадкової величини, яку задано таблицею за- дачі 2.33, обчислити і і зробити висновок про корельованість її компонент.

Розв’язання. Обчислимо коваріацію за формулою (2.72):

=

За формулою (2.73), маємо:

Оскільки то між заданими величинами і існує додатний кореляційний зв’язок.

У даній задачі величини і є залежні, бо як видно з їх закону розподілу .

Приклад 2.36. Для двовимірної випадкової величини (Х, Y), яка задана густиною задачі 2.34, обчислити і і зробити висновок про корельованість її компонент.

Розв’язання. У задачі 2.34 були обчислені чисельні характеристики складових даної двовимірної випадкової величини: , , За формулою (2.72):

+ ;

За формулою (2.73):

Оскільки то між заданими величинами і існує від’ємна кореляційна залежність.

Легко переконатися, що задані величини є залежні,бо

.

.

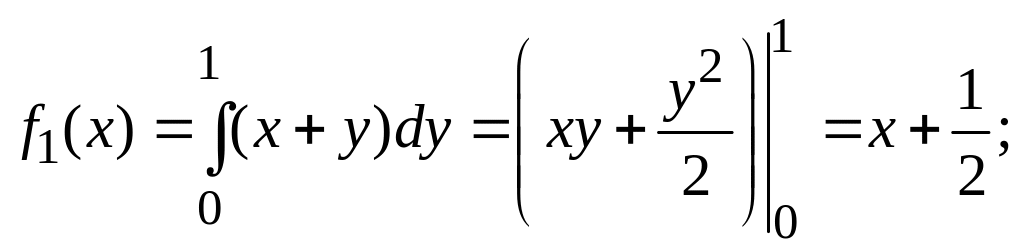
Отже, Х та Y є корельовані і залежні.

Приклад 2.37. Двовимірна випадкова величина задана густиною:

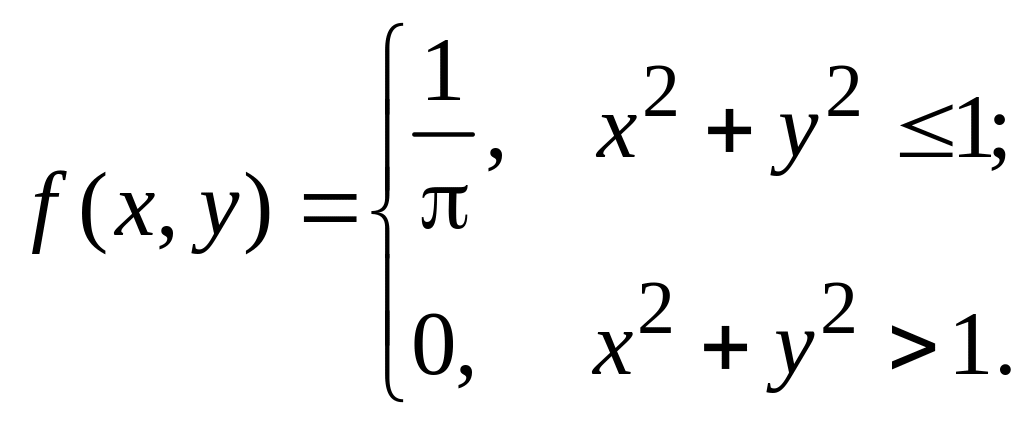
Обчислити і зробити висновок про корельованість випадкових величин Х і Y.

Розв’язання. З’ясуємо питання про залежність Х і Y:

,

,

,

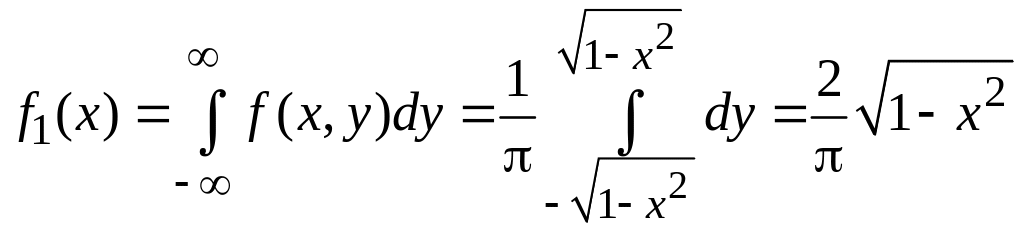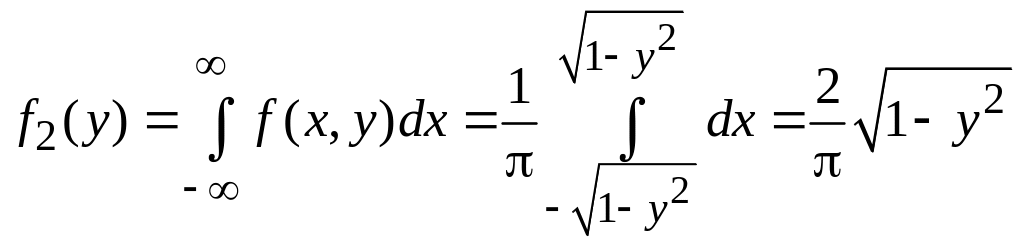що свідчить про залежність компонент Х і Y.

Знайдемо чисельні характеристики і :

;

,

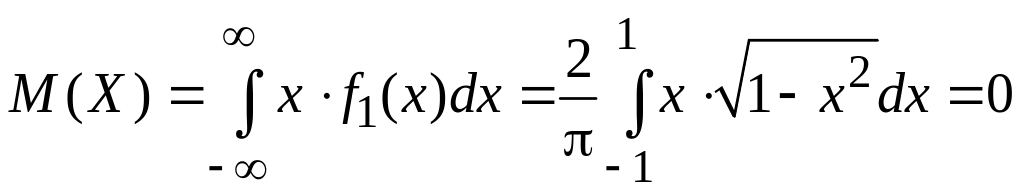бо у кожному випадку підінтегральна функція непарна і проміжок інтегрування симетричний відносно початку координат.

Кореляційний момент

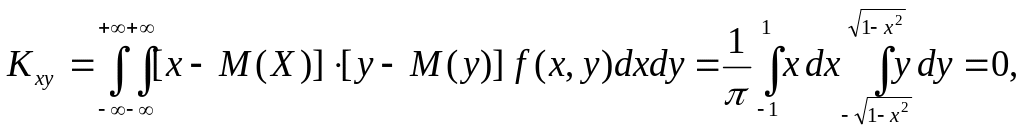
бо у внутрішньому інтегралі підінтегральна функція непарна і проміжок інтегрування симетричний відносно початку координат. Отже, , тобто випадкові величини Х і Y некорельовані і залежні.