2.4.1. Закон розподілу ймовірностей

Закон розподілу ймовірностей двовимірної випадко­вої величини, як і одновимірної, є її основною характеристикою.

А. В и п а д о к д и с к р е т н о ї в е л и ч и н и. Нехай – імовірність того, що дискретна випадкова величина набуде можливих значень Іншими словами, – імовірність того, що одночасно Х набуде значення і Y набуде значення , тобто , або .

Означення. Законом розподілу ймовірностей (законом розподілу) двовимірної дискретної випадкової величини називають перелік її можливих значень та відповідних їм імовірностей

Названий закон розподілу записують у формі таблиці (табл. 2.7).

Таблиця 2.7

Закон розподілу ймовірностей випадкової величини (Х, Y)

. . .	. . .	. . .	. . .	. . .	. . .
			…		1

Зазначимо, що закон розподілу дискретної випадкової величини має вигляд частини табл. 2.7, яка виділена жирними лініями. Останній рядок (стовпець) цієї таблиці задає розподіл одновимірної компоненти Х(Y).

Справді, розподіл одновимірної випадкової величини Х можна отримати, обчисливши за даними табл. 2.7 імовірності Р(Х = х_і), які позначимо через р(х_і). Для цього достатньо зауважити, що подію (Х = х_і ) можна представити як суму попарно несумісних подій:

звідки за правилом додавання ймовірностей несумісних подій одержимо:

і = 1, 2, …, п. (2.46)

Аналогічно можна побудувати розподіл одновимірної випадкової величини Y, обчисливши ймовірності

, j = 1, 2, …, т. (2.46)

Далі, оскільки кожна із систем подій або утворює повну групу попарно несумісних подій, то

. (2.47)

Приклад 2.26. Одночасно кидають гральний кубик і монету. Написати закон розподілу двовимірної випадкової величини , де Х – число очок, що випадуть на верхній грані кубика, – число появ герба на монеті.

Розв’язання. Випадкова величина Х може набути одного з чисел 1, 2, 3, 4, 5, 6, а випадкова величина – одного з чисел 0, 1. Звідси випливає, що – дискретна випадкова величина. Оскільки події і – незалежні, то

і закон розподілу дискретної випадкової величини має вигляд:

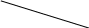
	1	2	3	4	5	6
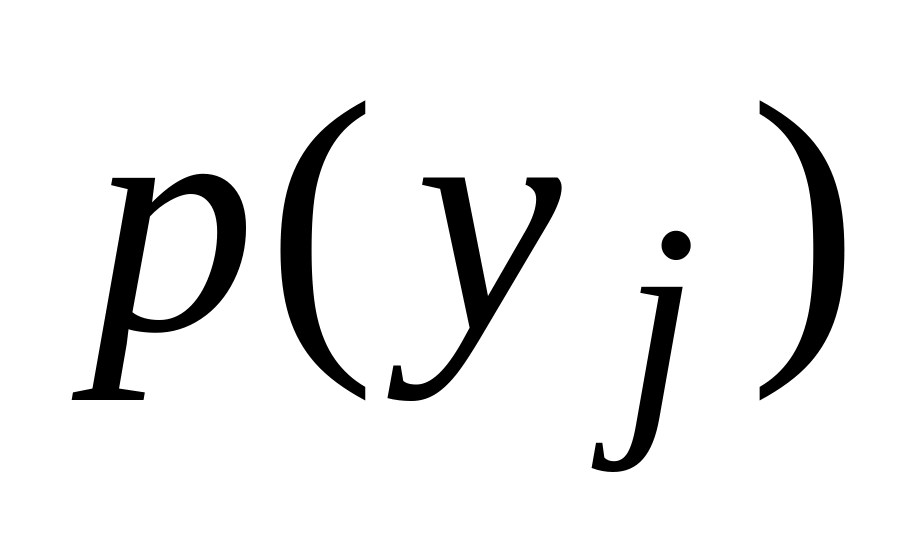
0	1/12	1/12	1/12	1/12	1/12	1/12	1/2
1	1/12	1/12	1/12	1/12	1/12	1/12	1/2
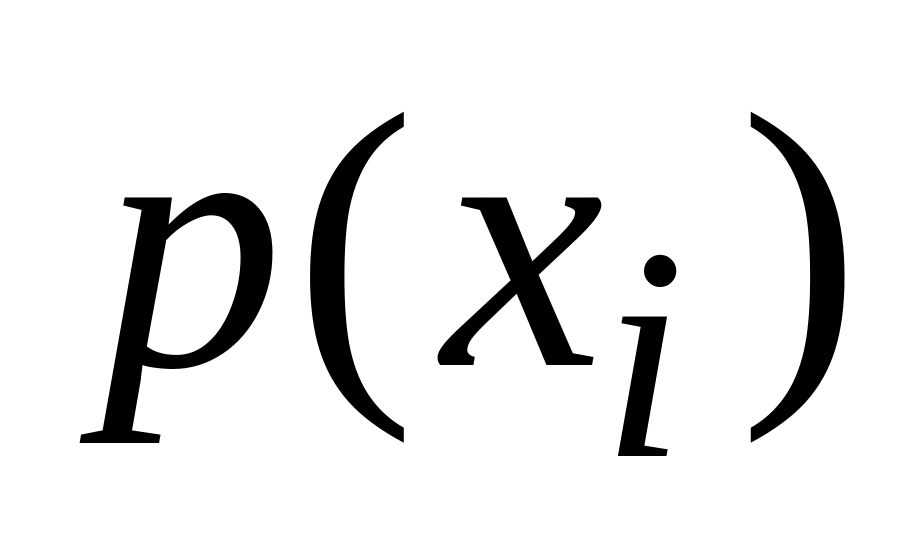
	1/6	1/6	1/6	1/6	1/6	1/6	1

Б. В и п а д о к н е п е р е р в н о ї в е л и ч и н и. Розподіл імовірностей двовимірної неперервної випадкової величини (X, Y), як і для одновимірної, визначається за допомогою функції або густини розподілу. Функцією розподілу ймовірностей можна характеризувати і дискретну дво­вимірну випадкову величину.

Означення. Функцією розподілу ймовірностей двовимірної випадкової величини (X, Y) називається функція , яка для будь-яких чисел х і y визначає ймовірність сумісної появи подій і , тобто:

F(x, y) = P(X < x, Y < y) = P(X < x ∩ Y < y). (2.48)

Іншими словами, функція розподілу двовимірної випадкової величини (X, Y) є ймовірність того, що її складова X набуде значення, меншого за число x, і складова Y набуде одночасно значення, меншого за число y.

Геометрично рівність (2.48) тлумачимо так: функція розподілу є ймовірністю того, що значення двовимірної випадкової величини (X, Y) (випадкові точки) попадають у безмежний прямокутник із вершиною (x, y), який розміщений нижче і лівіше від цієї вершини (рис. 2.14).

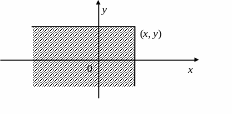
Рис. 2.14. Геометричне тлумачення двовимірної функції розподілу

Функція розподілу має такі властивості:

• значення функції розподілу задовольняють подвійну нерівність:

; (2.48)

• є неспадною функцією за кожним аргументом, тобто:

F(x₂, y) ≥ F(x₁, y), якщо х₂ > х₁;

F(x, y₂) ≥ F(x, y₁), якщо у₂ > у₁; (2.49)

• для функції виконуються граничні співвідношення:

, ; (2.50)

• якщо , функція розподілу двовимірної випадкової вели­чини 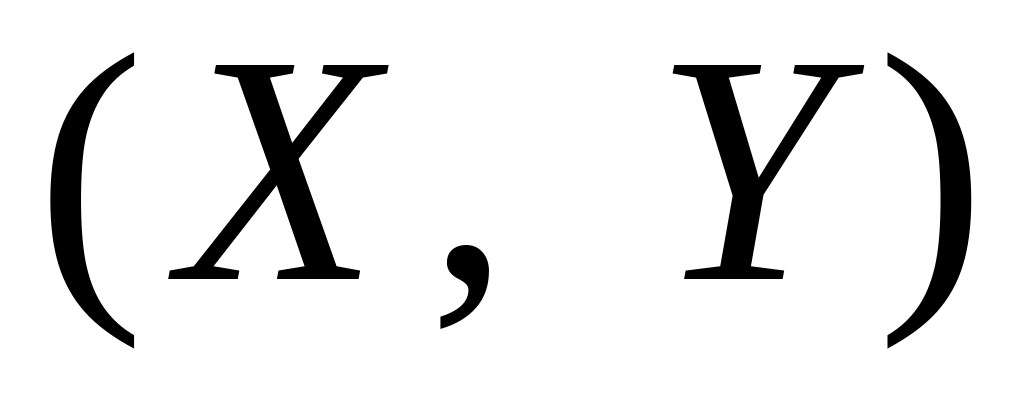наближається до функції розподілу 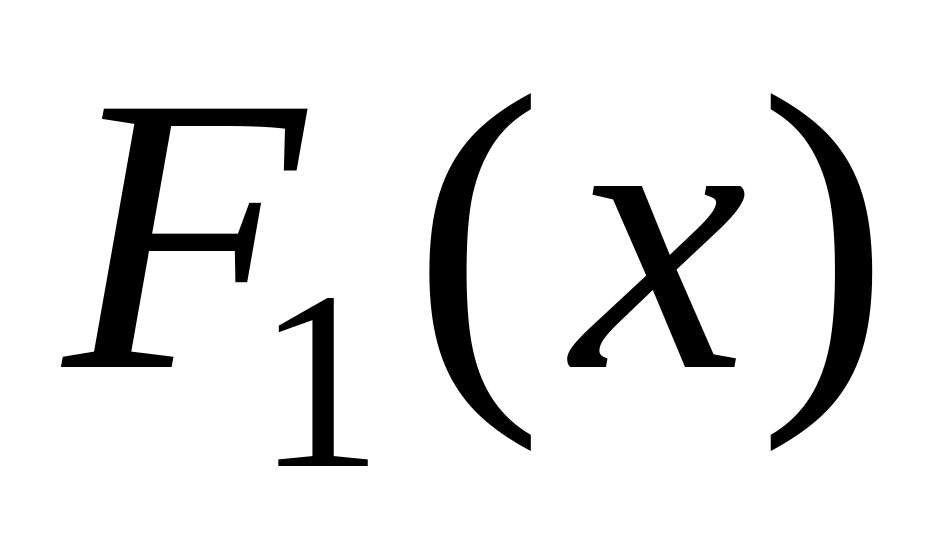складової X, а якщо – до функції розподілу 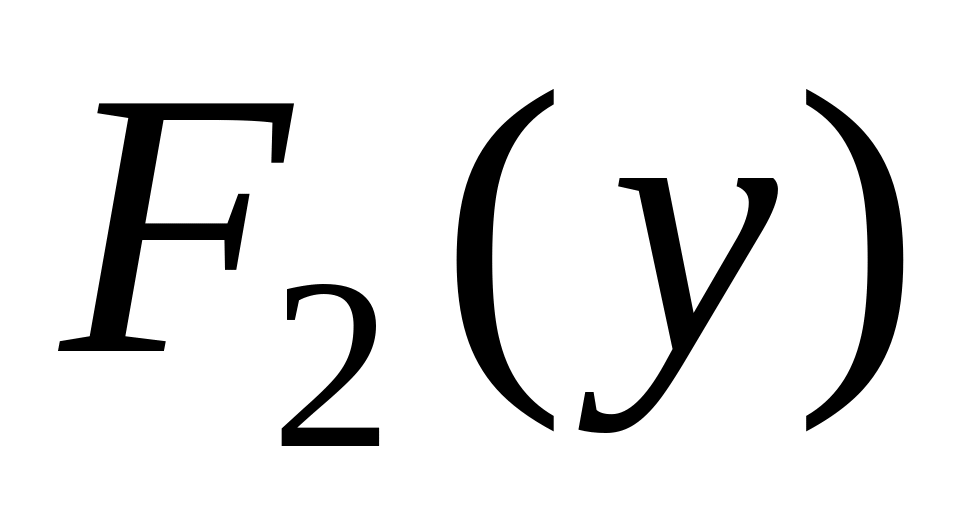складової Y, тобто:

; (2.51)

• імовірність попадання значень двовимірної випадкової величини 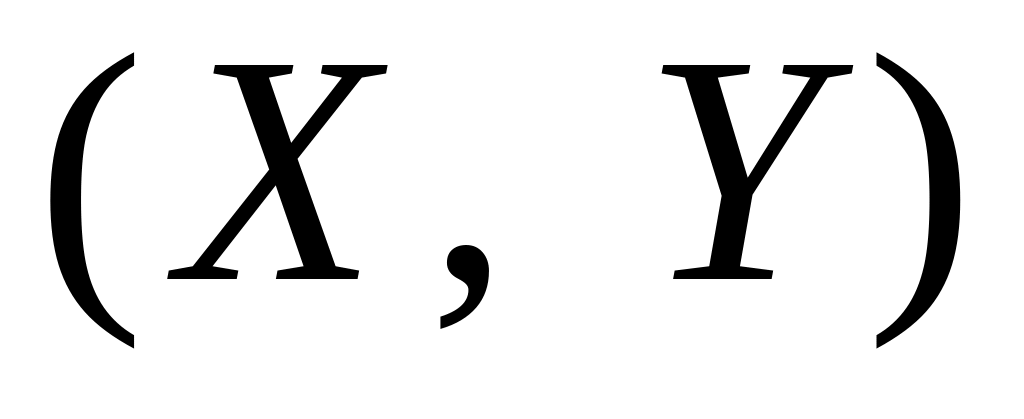у прямокутник 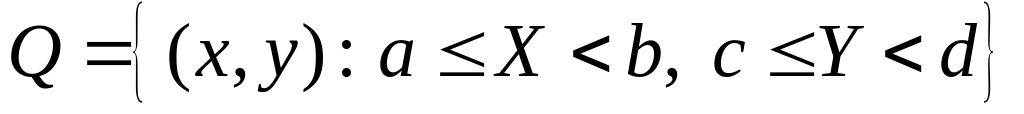обчислюється за формулою:

(2.52)

Сформульвані властивості двовимірної функції розподілу доводяться аналогічно як відповідні властивості одновимірної функції розподілу . Проілюструємо це доведенням співвідношень (2.50) і (2.51).

Співвідношення (2.50): рівності випливають з того, що відповідні сумісні події і , і , і є неможливі і їх імовірності дорівнюють нулю; рівність обумовлена тим, що сумісна подія і - вірогідна та її ймовірність дорівнює одиниці. Ці твердження мають наглядну геометричну інтерпретацію на рис. 2.14: якщо , то права сторона безмежного прямокутника переміщується необмежено вліво і при цьому імовірність попадання випадкової точки у цей прямокутник наближається до нуля. Аналогічну геометричну інтерпретацію маємо, коли або і .

Перше зі співвідношень (2.51) випливає з того, що подія є вірогідна і тому тобто у цьому випадку є імовірність події або функція розподілу складової X.

Аналогічно обгрунтовуємо друге співвідношення.

Зауваження. Якщо двовимірна випадкова величина (Х, Y) неперервна, то функція розподілу F(x, y) неперервна і для будь-яких дійсних чисел х₀ і y₀ імовірність Р(Х = х₀, Y = y₀) = 0. Звідси випливає, що в цьому випадку формулу (2.52) можна застосовувати також для обчислення ймовірностей:

Приклад 2.27. Функція розподілу ймовірностей двовимірної неперервної випадкової величини має вигляд:

Обчислити

Розв’язання. За формулою (2.52), враховуючи останнє зауваження, маємо:

Означення. Густиною (щільністю) розподілу ймовірностей двовимірної неперервної випадкової величини називають другу мішану похідну від її функції розподілу, тобто:

(2.53)

Густину розподілу ймовірностей двовимірної випадкової величини ще називають двовимірною густиною розподілу.

Густина (щільність) розподілу ймовірностей має такі властивості:

• густина розподілу ймовірностей невід’ємна: ;

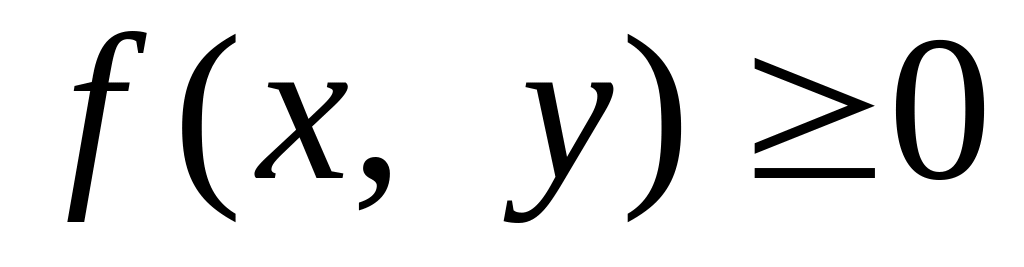• подвійний невласний інтеграл із безмежними межами інтегрування від двовимірної густини розподілу дорівнює одиниці:

. (2.54)

(Подвійний інтеграл (2.54) обчислюють так: спочатку обчислюють інтеграл за однією змінною, вважаючи другу сталою, а потім за другою змінною);

• якщо всі значення (х, у) двовимірної випадкової величини 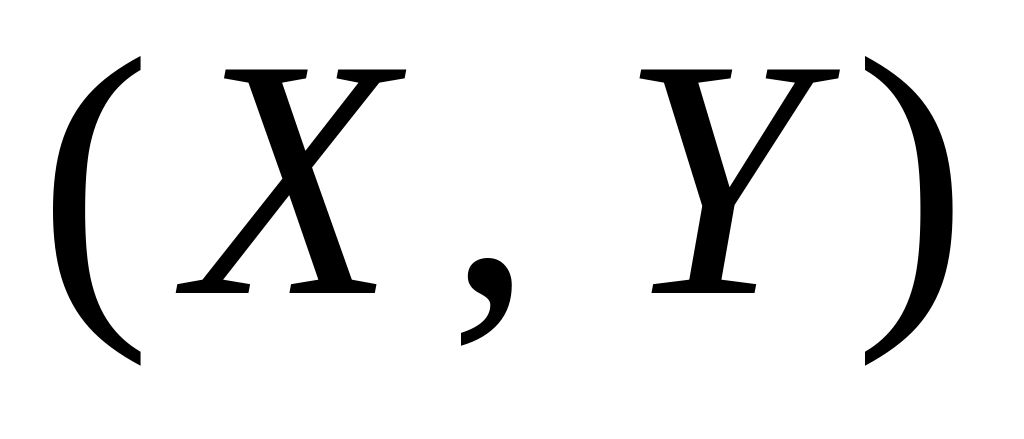містяться в прямокутнику 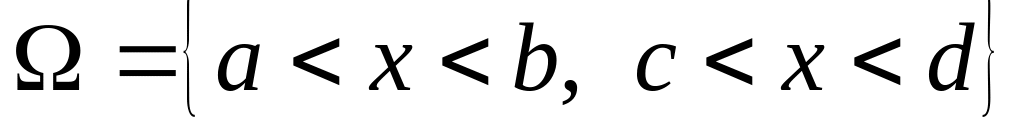і f(x, y) – густина її розподілу, то

(2.54)

• функція розподілу 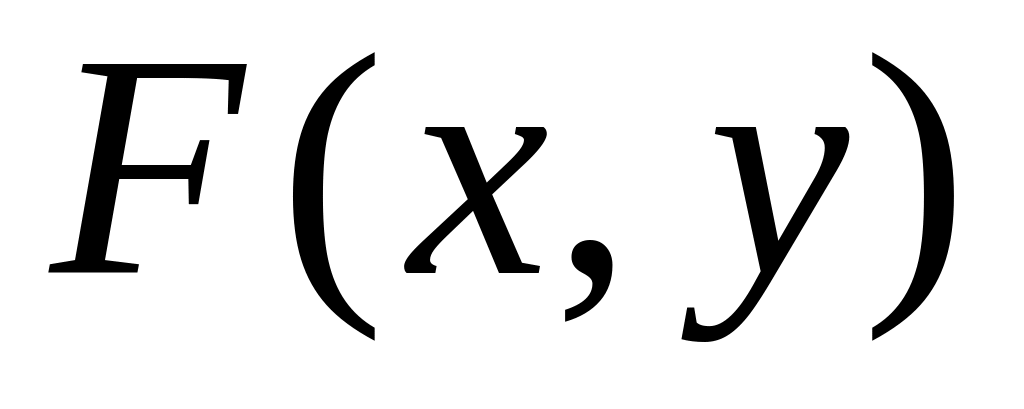двовимірної неперервної випадкової величини визначається за двовимірною густиною f(x, y) цієї величини за допомогою рівності:

(2.55)

• якщо можливі значення двовимірної неперервної випадкової величини 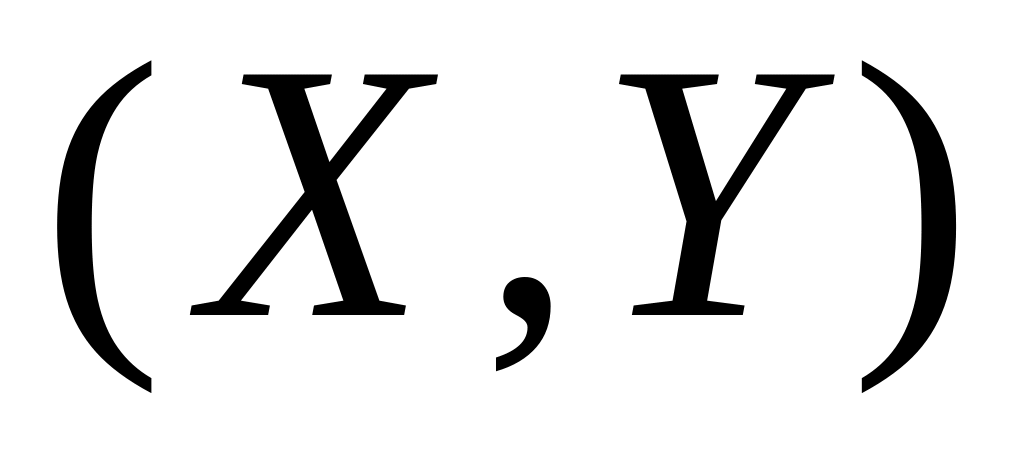розміщені в прямокутнику 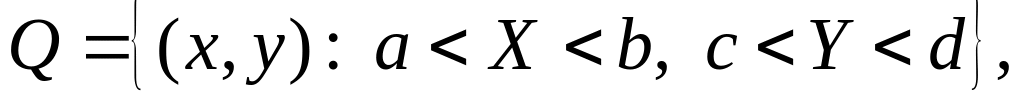то формула (2.55) набуває вигляду:

(2.55)

• імовірність попадання значень двовимірної неперервної випадкової величини (X, Y) у прямокутник виражається формулою:

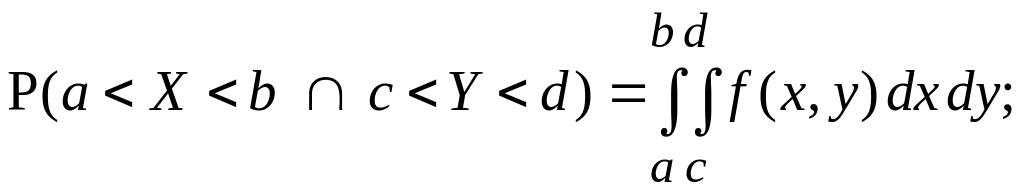(2.56)

• якщо f(x, y) – густина розподілу двовимірної випадкової величини (X, Y), то густини f₁(x) і f₂(y) розподілів одновимірних випадкових величин Х і Y відповідно визначаються за формулами:

(2.56)

Всі сформульвані властивості (крім останньої) двовимірної густини розподілу можна обгрунтувати аналогічними міркуваннями, як і у випадку густини розподілу одновимірної випадковї величини.

Обгрунтуємо перше зі співвідношень . Якщо - функція розподілу складової X, то її густина розподілу

.

Функція розподілу двовимірної випадкової величини (X, Y) виражається через густину її розподілу рівністю (2.55), з якої випливає, що

.

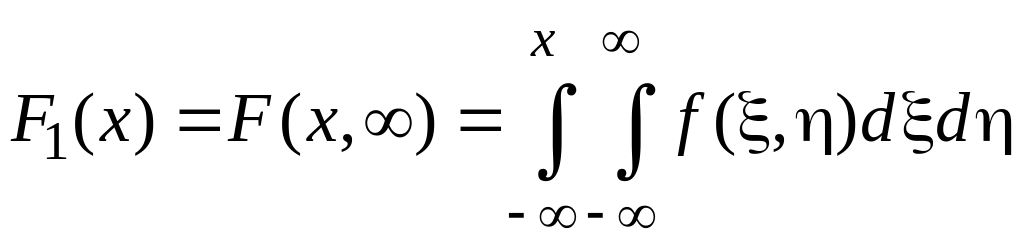Диференціюючи обидві частини одержаної рівності за х, одержимо:

.

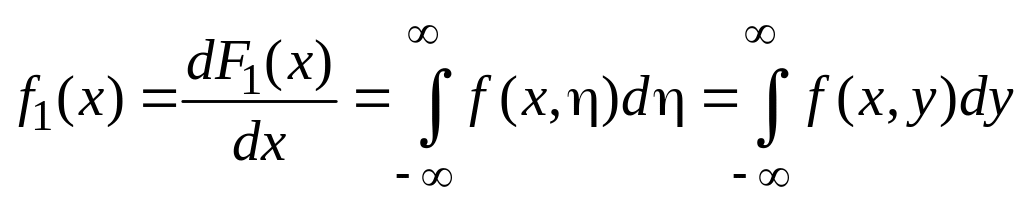Аналогічно обгрунтовуємо друге співвідношення.

Приклад 2.28. Двовимірна неперервна випадкова величина (X, Y) задана густиною розподілу:

де .

Знайти а і F(x, y). Обчислити .

Розв’язання. Сталу величину а визначаємо з умови (2.54):

Із знайденим значенням а двовимірна густина розподілу має вигляд:

Функцію розподілу F(x, y) описаної в задачі двовимірної випадкової величини знаходимо за формулою (2.55). Розглянемо випадки:

а)

б)

=

в)

г)

=

д)

=

Отже, функція розподілу F(x, y) записується так:

Шукану ймовірність обчислюємо за формулою (2.56):

= .

Оскільки функція розподілу F(x, y) відома, то цю ймовірність можна також об­числити за формулою (2.52).