Нехай задана послідовність випадкових величин:

Х₁, Х₂, ..., Х_п, ...

Кажуть, що ця послідовність збігається за ймовірністю до невипадкової величини а, якщо за необмеженого збільшення п імовірність події (де  > 0 – як завгодно мале фіксоване число) наближається до одиниці, тобто:

.

Іншими словами, якими б не були як завгодно малі наперед задані числа  > 0 і  > 0, завжди можна знайти таке велике число N, що для всіх номерів п, більших за N, виконується нерівність:

2.3.3. Теорема Чебишова і стійкість середнього арифметичного випадкових величин

Теорема. Нехай випадкові величини , … попарно незалежні, мають скінченні математичні сподівання = а_і та обмежені в сукупності дисперсії , і = 1, 2, ... . Позначимо:

Тоді для будь-якого числа

(2.42)

тобто різниця між середнім арифметичним випадкових величин і середнім арифметичним їх математичних сподівань збігається за ймовірністю до нуля.

Суть теореми Чебишова полягає в тому, що хоч окремі випадкові величини можуть набувати значень, досить віддалених від своїх математичних сподівань а_і, зате середнє арифметичне великого числа цих випадкових величин із імовірністю, близькою до одиниці, набуває значення, яке близьке до середнього арифметичного їх математичних сподівань. Тобто середнє арифметичне великого числа незалежних випадкових величин втрачає випадковий характер і має властивість стійкості.

Теорема Чебишова знаходить важливе практичне застосування. Зокрема, на цій теоремі ґрунтується вибірковий метод, який широко використовується в статистиці. Суть його полягає в тому, що на підставі вивчення певної ознаки для достатньо великої випадкової вибірки об’єктів роблять висновок про всю їх сукупність (генеральну сукупність).

Наслідок із теореми Чебишова. Якщо всі члени послідовності незалежних однаково розподілених випадкових величин мають скінченні математичні сподівання M(X_i) = a і дисперсії то для будь-якого  > 0

, (2.42)

тобто середнє арифметичне випадкових величин збігається за ймовірністю до математичного сподівання а.

2.3.4. Теорема Бернуллі і стійкість відносних частот

Теорема. Нехай – число появ події А в незалежних спро­бах Бернуллі, – відносна частота цієї події, P(A) = p – імовір­ність появи події А в одній спробі. Тоді для будь-якого  > 0

(2.43)

тобто відносна частота події А збігається за ймовірністю до її ймовірності р.

Із твердження теореми Бернуллі випливає, що коли число випробувань п є достатньо великим, то для будь-якого числа подія є практично вірогідною, тобто відносна частота події А має властивість стійкості.

Зазначимо, що теорему Бернуллі можна розглядати як окремий випадок наведеного вище наслідку з теореми Чебишова, оскільки випадкова величина може бути представлена сумою незалежних однаково розподілених випадкових величин:

Хі	0	1
р	q	р

, q = 1 – p, М(Х_і) = р, і = 1, 2, ... . Це означає, що в теоремі Бернуллі йдеться про збіжність середнього арифметичного випадкових величин Х_і до математичного сподівання величини Х_і, тобто до ймовірності р = Р(А).

Зауважимо також, що в умовах теореми Бернуллі нерівність Чебишова, застосована до випадкової величини має вигляд:

(2.43)

Зауваження. На підставі теореми Бернуллі не слід робити висновок, що Остання рівність означає, що для всіх де – деяке велике натуральне число і – як завгодно мале число. А теорема Бернуллі тільки стверджує, що ймовірність є близькою до одиниці при досить великих п, а нерівність для деяких навіть великих п може не виконуватися.

Приклад 2.22. Використовуючи нерівність (2.43), установити, яке число n експериментів треба провести, щоб відхилення відносної частоти появ події А від імовірності за абсолютною величиною було меншим за з імовірністю, не меншою за 0,9. Отриманий результат порівняти з оцінкою для п, обчисленою за допомогою інтегральної формули Лапласа.

Розв’язання. За умовою задачі Із нерівності (2.43) маємо:

тобто заданого відхилення відносної частоти події від її ймовірності буде досягнуто, якщо проведемо не менше ніж, 16 000 випробувань.

Застосуємо тепер для оцінки ймовірності заданого відхилення формулу (1.31). Одержимо:

.

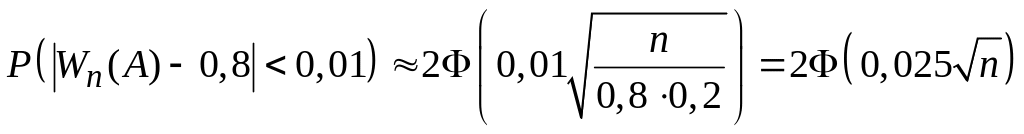За умовою задачі:

За таблицею значень інтегральної функції Лапласа знайдемо . Ураховуючи останню нерівність та беручи до уваги, що функція Ф(х) – монотонно зростаюча, маємо:

Звідси шукане число випробувань

Отже, у даному випадку, як і в прикладі 2.21, застосування нерівності Чебишова дає грубу оцінку.