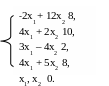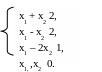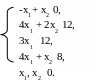1.5.2 Решить задачи графическим методом

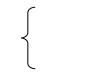
2.1 => max (min),	2.2 Z(x) = -2x1 + 5x2 → max (min) -3x1 + 2x2 12 x1 + 2x2 = 8 x1 + x2 5 x1, x2 0
2.3 Z (x) = x1 + 6x2 → max (min)	2.4 => max (min)
2.5 Z (x) = x1 + x2 → max (min)	2.6 Z (x) = -2x1 + 6x2 → max (min)

2 Симплексный метод решения задачи линейного программирования

ВВЕДЕНИЕ

Среди универсальных методов решения задач линейного программирования наиболее распространен симплексный метод.

Общая идея симплексного метода (ме­тода последовательного улучшения плана) для решения ЗЛП состоит:

1. умение находить начальный опорный план;

2. наличие признака оптимальности опорного пла­на;

3. умение переходить к нехудшему опорному плану.

2.1 Цель

Усвоить алгоритм решения задач линейного программирования симплексным методом, М-метод.

2.2 Задачи

Приобрести навыки составления простейших математических моделей, решить их симплексным методом задачи, провести анализ решения.

2.3 Алгоритм решения

Предварительный шаг: приведение задачи к каноническому виду.

Основу алгоритма симплексного метода составляет последовательность итераций и шагов, реализующих идеи симплексного метода и обеспечивающих переход от одного базисного решения к другому до получения оптимального решения, либо вывода о том, что задача не имеет решения.

1. Выбираем m переменных, задающих допустимое пробное решение и исключим эти переменные из целевой функции.

2. Проверяем нельзя ли за счет одной из переменных приравненной к нулю (небазисной), улучшить значение целевой функции, придавая ей отличные от нуля значения. Если это, возможно, перейдем к третьему этапу, в противном случае прекратим вычисления.

3. Найдем предельное значение переменной, за счет которой можно улучшить значение целевой функции. Увеличение значения этой переменной допустимо до тех пор, пока одна из m переменных, вошедших в пробное решение не обратится в нуль.

4. Разрешим систему из n уравнений относительно переменной, вошедшей в новое пробное решение. Вернемся ко второму этапу.

2.4 Пример решения задачи

Найти оптимальное сочетание посевов пшеницы и сахарной свеклы, обеспечивающий максимум прибыли. Под эти культуры хозяйство выделило ресурсы 1000 га пашни, 18000 чел.- дней труда, 3000 ц минеральных удобрений. В таблице 2.1 представлены исходные показатели.

Таблица 2.1 Исходные показатели

Показатели	Пшеница	Сахарная свекла
Труд, чел.-дней Минеральное удобрение, ц Прибыль, тыс.руб.	7 2 150	40 9 300

Решение.

Переменные:

Х₁ – площадь под пшеницу, га;

Х₂ – площадь под сахарную свеклу, га.

Ограничения:

1. По площади пашни, га

X₁ +Х₂ ≤ 1000,

2. По затратам труда, чел.-дней

7Х₁ +40Х₂ ≤ 18000;

3. По использованию минеральных удобрений, ц

2Х₁ +9Х₂ ≤ 3000;

Z (мах прибыли, руб.) =150Х₁ +300Х₂ → max.

Решение задачи

Предварительный шаг. Приведем к каноническому виду:

7 х₁ +40х₂ +х₃ =18000,

2х₁ +9х₂ +х₄ =3000,

х₁ +х₂+х₅ =1000.

Х₁ , Х₂  0,

Z =150х₁ +300х₂+ 0х₃ +0х₄ +0х₅ → max.

Интерация 1.

Шаг1. Выписываем исходное допустимое базисное решение и соответствующее ему значение целевой функции.

х₃, х₄, х₅ – базисные переменные.

х₁ х₂ х₃ х₄ х₅

Х = 0 0 18000 3000 1000

Z = 150·0+300·0+0·18000+0·300+0·1000 = 0.

Шаг2. Проверяем оптимальность полученного решения. Если решение не оптимально, то переходим к шагу 3. В противном случае записываем ответ.

Пусть ∆ х₁ =1, тогда ∆ х₃ =-7, ∆ х₄ =-2, ∆ Х₅ =-1

∆Z=150·1+300·0+0·(-7)+0·(-2)+0·(-1)=150. Так как ∆Z  0, то переменную х₁ целесообразно ввести в базис.

Шаг3. Определяем, какая из прежних базисных переменных должна быть выведена из базиса.

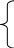х₃  0 х₃ =18000 - 7х_1, 18000 - 7х₁ 0, х₁  257,1,

х₄  0 х₄ =300 - 2х_1, 300-2х₁  0, х₁  1500,

х₅  0 х₅ =100 – х_1, 100 – х₁  0, х₁  100.

Решением системы неравенств является третье неравенство, поэтому из базиса выводим переменную х₅.

Шаг 4. Пересчитываем систему уравнений задачи с учетом нового состава базисных переменных.

3 уравнение х₁ +х₂+х₅ =1000,

1 уравнение _7х₁ +40х₂ +х₃ =18000

7х₁ +7х₂+7х₅ =7000

33х₂ +х₃ - 7х₅ =11000,

2 уравнение _2х₁ +9х₂ +х₄ =3000

2х₁ +2х₂+2х₅ =2000

7х₂+х₄ - 2х₅ = 1000.

В результате имеем следующую систему уравнений:

33х₂ +х₃ - 7х₅ = 11000,

7х₂+х₄ - 2х₅ = 1000,

х₁ +х₂+х₅ =1000.

Итерация 2.

Шаг1. Выписываем исходное допустимое базисное решение.

х ₃, х₄, х₁ – базисные переменные.

х₁ х₂ х₃ х₄ х₅

Х = 1000 0 11000 1000 0

Z=150·1000+300·0+0·11000+0·1000+0·0=150000

Шаг2. Проверяем оптимальность полученного решения.

Пусть ∆ х₂ =1, тогда ∆ х₃ =-33, ∆ х₄ = -7, ∆ Х₅ = -1

∆Z=150·(-1)+300·1+0·(-33)+0·(-7)+0·0=150. Так как ∆Z  0, то переменную х₂ целесообразно ввести в базис.

Шаг 3. Определяем, какая из прежних базисных переменных должна быть выведена из базиса.

х₃  0 х₃ =11000 - 33х_2, 11000 – 33х₂  0, х₂  333,3,

х₄  0 х₄ =1000 - 7х_2, 1000 -7х₂  0, х₂  142,9,

х₁  0 х₁ =1000 – х_2, 1000 – х₂  0, х₂  1000.

Переменную х₄ выводим из базиса.

Шаг4. Пересчитываем систему уравнений задачи с учетом нового состава базисных переменных.

2 уравнение 7х₂+х₄ - 2х₅ = 1000,

х₂+1/7х₄ – 2/7х₅ = 1000/7,

3 уравнение _х₁ +х₂+х₅ =1000

х₂+1/7х₄ – 2/7х₅ = 1000/7

х₁- 1/7х₄ +9/7х₅ = 857,4,

1 уравнение _33х₂ +х₃ - 7х₅ = 11000

33х₂+33/7х₄ – 66/7х₅ = 33000/7

х₃ – 67,15х₄ + 2,42х₅ = 6285,7.

В результате имеем следующую систему уравнений:

х₃ – 67,15х₄ + 2,42х₅ = 1571,5,

х₂+1/7х₄ – 2/7х₅ = 1000/7,

х₁- 1/7х₄ +9/7х₅ = 6285,7.

Итерация 3.

Шаг1. Выписываем исходное допустимое базисное решение.

х ₃, х₂, х₁ – базисные переменные.

х₁ х₂ х₃ х₄ х₅

Х = 857,4 142,9 6285,7 0 0

Z=150·857,4+300·142,9+0·6285,7+0·0+0·0 = 171429.

Шаг2. Проверяем оптимальность полученного решения.

Пусть ∆ х₄ =1, тогда ∆ х₃ = 67,15, ∆ х₂ = -1/7, ∆ Х₁ = -1/7.

∆Z=150·(-1/7)+300·(-1/7)+0·67,15+0·1+0·0 = -64,3. Так как ∆Z ≤ 0, то переменную х₄ нецелесообразно вводить в базис.

Пусть ∆ х₅ =1, тогда ∆ х₃ = -66/7, ∆ х₂ = 2/7, ∆ Х₅ = -9/7.

∆Z=150·(-9/7)+300·(2/7)+0·66/7+0·0+0·1= -107,4. Так как ∆Z ≤ 0, то переменную х₅ нецелесообразно вводить в базис.

Поскольку на данной итерации ни одну из небазисных переменных нецелесообразно вводить в базис, решение оптимально.

Ответ: Прибыль будет равна 171429 руб., если посевная площадь под пшеницу составит 857,4 га и сахарную свеклу 142,9 га.