
- •Основи теорії ймовірностей і статистичні методи обробки даних у психологічних і педагогічних експериментах.– Львів: Видавничий центр лну імені Івана Франка, 2006. – 168 с.
- •І. Основи теорії ймовірностей
- •Формула повної ймовірності
- •Формули Байєса
- •Задачі до розділу і.
- •Іі. Випадкова величина Поняття випадкової величини
- •Функція розподілу випадкової величини
- •Щільність розподілу неперервно розподіленої випадкової величини
- •Характеристики розподілу випадкової величини
- •Математичне сподівання випадкової величини
- •Дисперсія та стандартне відхилення випадкової величини. Асиметрія і ексцес.
- •Квантилі
- •Деякі дискретні розподіли Розподіл Бернуллі
- •Біномний розподіл
- •Апроксимаційні формули Муавра-Лапласа Локальна теорема Муавра-Лапласа Якщо у схемі Бернулі величина , коли , то
- •Функція розподілу двовимірної випадкової величини
- •Умовні закони розподілу
- •Коваріація і коефіцієнт кореляції
- •Коваріаційна матриця і матриця парних кореляцій
- •Граничні закони теорії ймовірностей Нерівність Чебишева
- •Теорема Чебишева
- •Закон Бернуллі
- •Теорема Ляпунова
- •Задачі до розділу іі.
- •Ііі. Елементи математичної статистики
- •Генеральна сукупність і вибірка
- •Дискретний варіаційний ряд
- •Інтервальний варіаційний ряд
- •Точкові та інтервальні оцінки
- •Поняття про статистичну перевірку гіпотез
- •Задачі до розділу ііі.
- •Іv. Методи математичної обробки даних у психології Ознаки і змінні. Шкали вимірювання ознак
- •Перевірка гіпотези про однорідність вибірки
- •Перевірка гіпотези про узгодженість розподілів
- •Критерій Пірсона
- •Критерій Колмогорова
- •Критерій Смирнова
- •Перевірка гіпотези про рівність двох дисперсій
- •Виявлення відмінностей у рівні досліджуваної ознаки Критерій Розенбаума
- •Критерій Манна-Уітні
- •К ритерій Стьюдента
- •І. Вибірки взяті з однієї генеральної сукупності
- •Іі. Вибірки взяті з різних генеральних сукупностей
- •Перевірка наявності зсуву у значеннях досліджуваної ознаки
- •Критерій знаків
- •Критерій Вілкоксона
- •Парний t-тест Стьюдента
- •Перевірка впливу фактора на зміну рівня досліджуваної ознаки
- •Критерій Краскела-Уоллеса
- •Критерій тенденцій Джонкхієра
- •Критерій Фрідмана
- •К ритерій тенденцій Пейджа
- •Однофакторний дисперсійний аналіз
- •П еревірка наявності зв’язку між двома ознаками
- •Зв'язок ознак, виміряних у номінативних шкалах
- •Зв'язок ознак, виміряних у порядкових шкалах
- •Зв'язок ознак, виміряних в інтервальних шкалах
- •Задачі до розділу іv.
- •Критичні значення розподілу
- •Критичні значення розподілу Фішера-Снедекора
- •Критичні значення критерію Розенбаума
- •Критичні значення критерію Манна-Уітні
- •Критичні значення критерію знаків
- •Критичні значення критерію Вілкоксона
- •Критичні значення критерію Краскела-Уоллеса
- •Критичні значення критерію Джонкхієра
- •Критичні значення критерію Фрідмана
- •Критичні значення критерію Пейджа
- •Критичні значення рангового коефіцієнта кореляції Спірмена
- •Д о д а т о к 2: Елементи вищої математики Матриці, визначники, системи лінійних рівнянь Поняття матриці. Операції над матрицями.
- •Визначник матриці. Обернена матриця
- •Системи лінійних алгебричних рівнянь
- •Вступ до математичного аналізу
- •Числові послідовності та їх границі
- •Границя функції в точці. Односторонні границі
- •Неперервність функції
- •Диференціальне числення функцій однієї змінної Похідна функції в точці
- •Диференційовність функції
- •Монотонність функції. Екстремуми
- •Похідні вищих порядків
- •Інтегральне числення функцій однієї змінної Первісна функції. Невизначений інтеграл
- •В изначений інтеграл
- •Невластиві інтеграли
- •Частинні похідні функцій багатьох змінних
- •Д о д а т о к 3: Деякі команди Maple 8.
- •Алфавітний покажчик
- •Основи теорії ймовірностей і статистичні методи аналізу даних у психологічних і педагогічних експериментах
Д о д а т о к 2: Елементи вищої математики Матриці, визначники, системи лінійних рівнянь Поняття матриці. Операції над матрицями.
Матрицею розмірності m n називають прямокутну таблицю чисел, яка складається з m рядків і п стовпчиків. Числа, які утворюють матрицю називають елементами матриці. Матриці позначають великими літерами латинського алфавіту, а їх елементи відповідними малими літерами з індексами. Наприклад,
 .
.
Дві матриці
називаються рівними, якщо вони мають
однакову розмірність і їх відповідні
елементи рівні.
![]() .
.
Матриця,
яка складається з одного рядка (одного
стовпчика) називається вектор-рядком
(вектор-стовпчиком). Як правило
замість
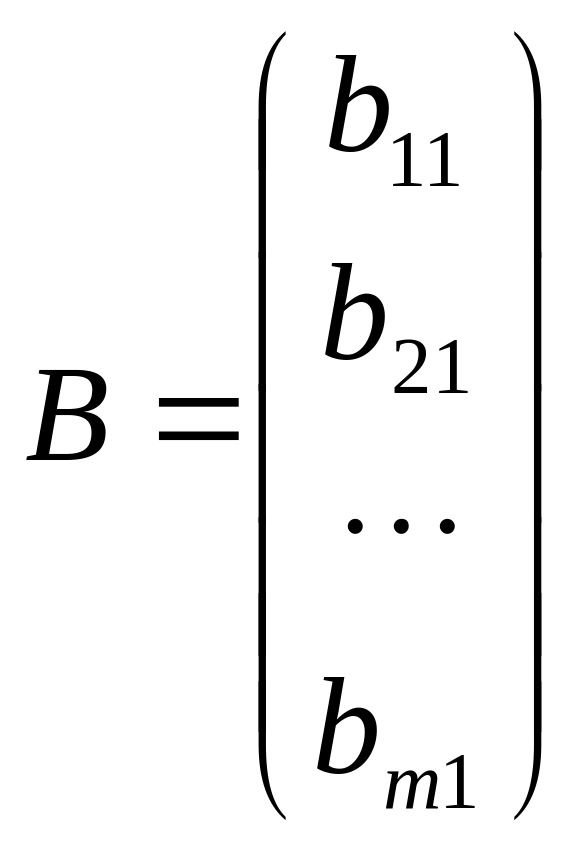 або
або
![]() відповідно пишуть
відповідно пишуть
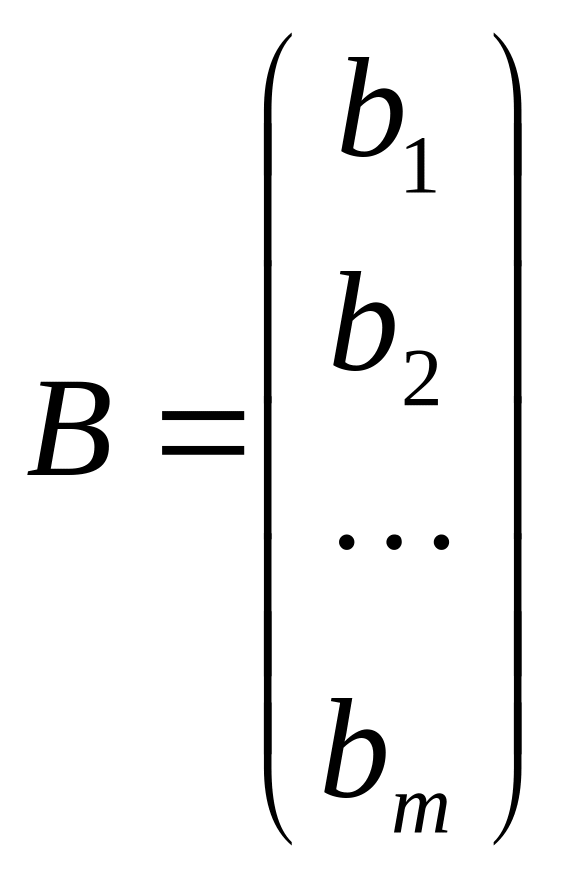 та
та
![]() .
.
Квадратною
матрицею п-го порядку називається
матриця, яка складається з п рядків
і п стовпчиків. Наприклад,
![]() — квадратна матриця 2-го порядку.
Квадратна матриця, всі елементи якої
дорівнюють нулеві, називається
— квадратна матриця 2-го порядку.
Квадратна матриця, всі елементи якої
дорівнюють нулеві, називається
нуль-матрицею.
Елементи
![]() квадратної матриці п-го порядку
називаються діагональними і утворюють
головну діагональ матриці. Матриця,
всі елементи якої окрім діагональних
дорівнюють нулеві, називається
діагональною. Діагональну матрицю,
у якої всі діагональні елементи дорівнюють
одиниці, називають одиничною і
позначають буквою Е.
квадратної матриці п-го порядку
називаються діагональними і утворюють
головну діагональ матриці. Матриця,
всі елементи якої окрім діагональних
дорівнюють нулеві, називається
діагональною. Діагональну матрицю,
у якої всі діагональні елементи дорівнюють
одиниці, називають одиничною і
позначають буквою Е.
Добутком
матриці
![]() на число
називатимемо матрицю
на число
називатимемо матрицю
![]() ,
кожен елемент якої дорівнює відповідному
елементу матриці А, помноженому на
скаляр . Наприклад,
якщо
,
кожен елемент якої дорівнює відповідному
елементу матриці А, помноженому на
скаляр . Наприклад,
якщо
![]() ,
то
,
то
![]() .
Матрицю –А=–1А
називають протилежною до матриці
А.
.
Матрицю –А=–1А
називають протилежною до матриці
А.
Сумою матриць
![]() і
і
![]() однакової розмірності називають матрицю
однакової розмірності називають матрицю
![]() ,
кожен елемент якої дорівнює сумі
відповідних елементів матриць А і
В. Наприклад, якщо
,
кожен елемент якої дорівнює сумі
відповідних елементів матриць А і
В. Наприклад, якщо
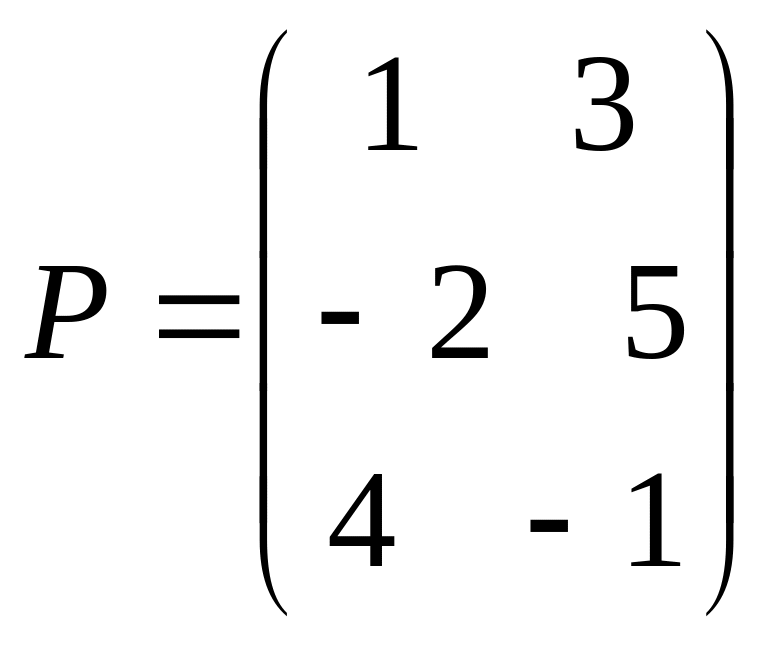 ,
а
,
а
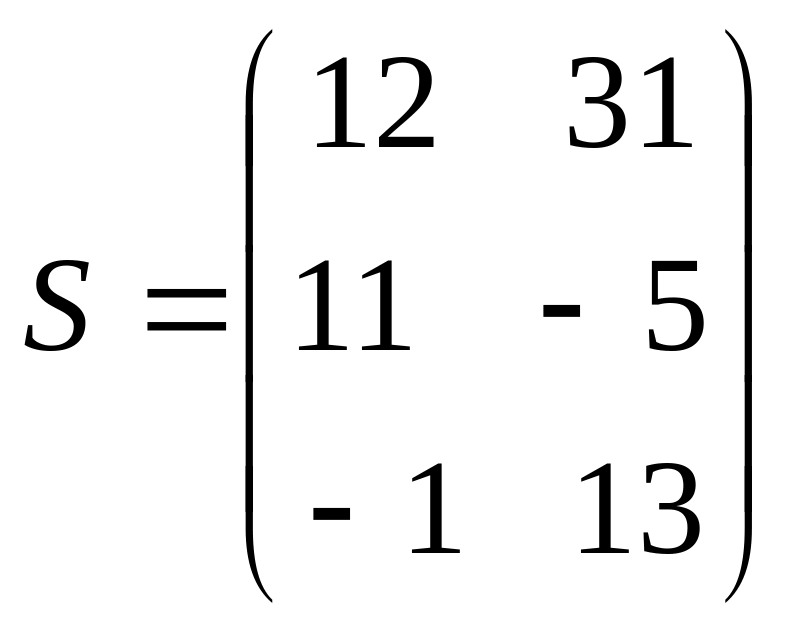 ,
то
,
то
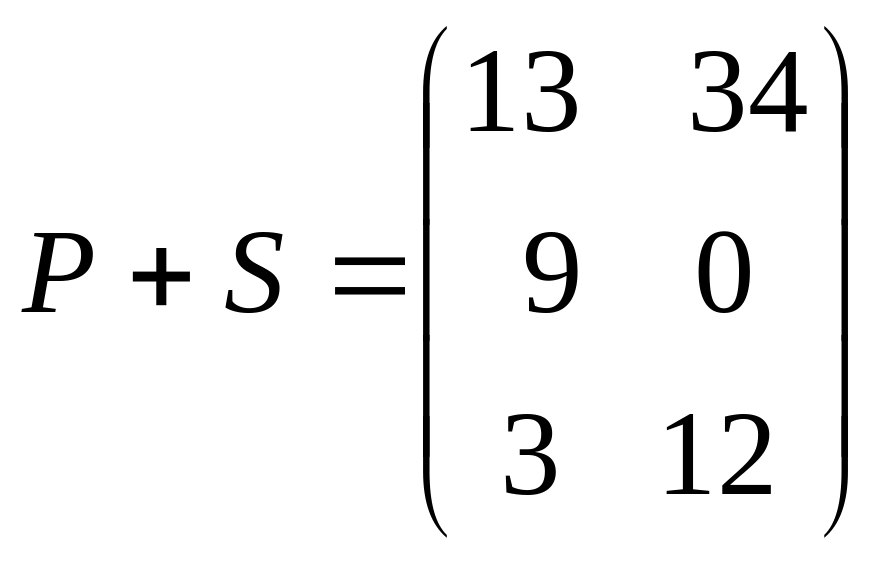 .
.
Добутком
матриці
розмірності т п
на матрицю
![]() розмірності п р
називають матрицю
розмірності п р
називають матрицю
 розмірності т р,
кожен елемент якої є сумою добутків
елементів відповідного рядка матриці
А на відповідний стовпчик матриці
В. Наприклад, якщо
розмірності т р,
кожен елемент якої є сумою добутків
елементів відповідного рядка матриці
А на відповідний стовпчик матриці
В. Наприклад, якщо
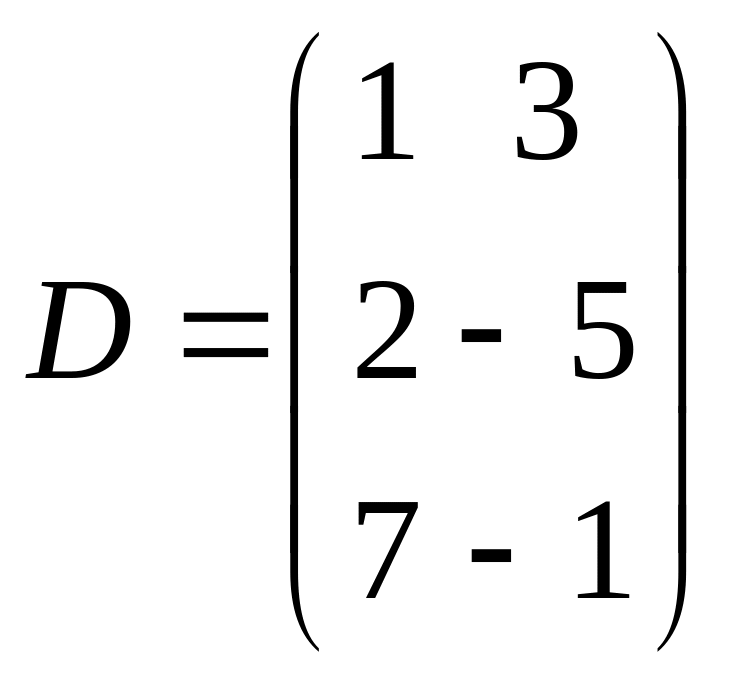 ,
а
,
а
![]() ,
то
,
то
![]() .
.
Зауважимо, що добуток матриць є некомутативною операцією. Так в останньому прикладі добуток FD не існує, оскільки кількість стовпчиків матриці F не дорівнює кількості рядків матриці D. Але навіть якщо обидва добутки
існують, вони, як правило, не рівні між
собою. Наприклад,![]() ,
але
,
але
![]() .
.
Справджуються такі властивості:
1)
2)
3)
7)
8)
9)
|
4)
5)
6)
10)
11)
12)
|
Матриця
![]() називається транспонованою до
матриці
.
Очевидно, що коли розмірність матриці
А дорівнює тп,
то розмірність транспонованої матриці
— пт.
Наприклад, якщо
називається транспонованою до
матриці
.
Очевидно, що коли розмірність матриці
А дорівнює тп,
то розмірність транспонованої матриці
— пт.
Наприклад, якщо
![]() ,
то
,
то
![]() .
.
Справджуються такі властивості операції транспонування:
1)
2)
|
3) 4)
|
Визначник матриці. Обернена матриця
Для квадратних матриць вводиться поняття визначника (або детермінанта) матриці.
Визначником матриці
![]() першого порядку будемо називати
елемент цієї матриці:
першого порядку будемо називати
елемент цієї матриці:
![]() .
.
Визначником матриці
![]() другого порядку будемо називати число
другого порядку будемо називати число
![]() .
Наприклад,
.
Наприклад,
![]()
Визначником матриці
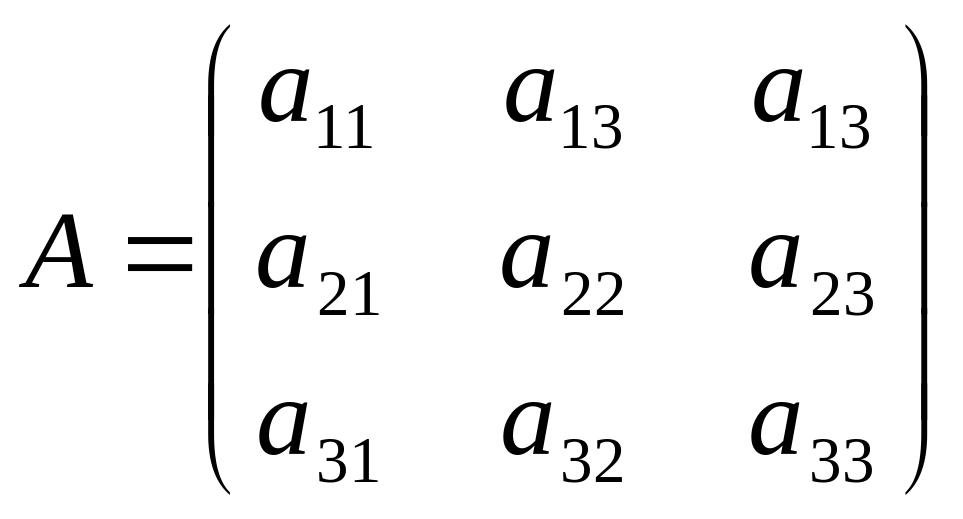 третього порядку будемо називати
число
третього порядку будемо називати
число
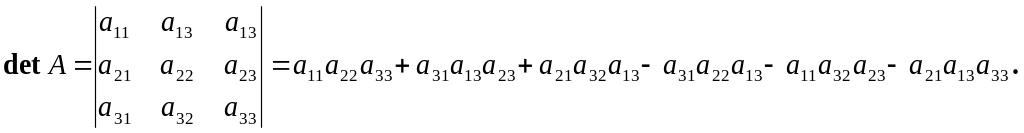
Наприклад,
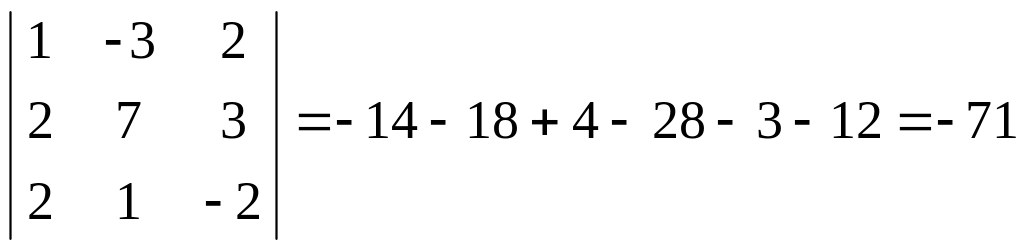 .
.
Визначникам матриць притаманні такі властивості:
Визначник одиничної матриці дорівнює одиниці
![]() .
.
Якщо який–небудь рядок (стовпчик) матриці складається з одних нулів, то визначник матриці дорівнює нулеві.
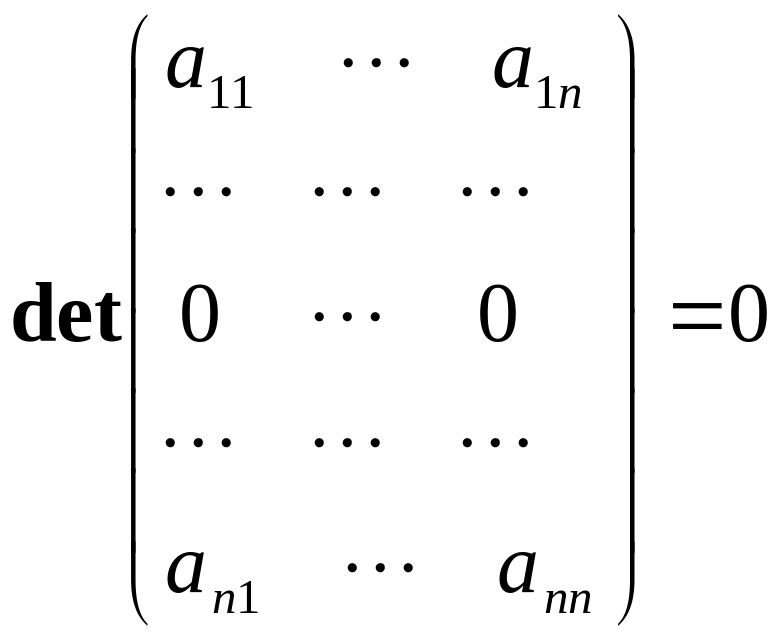 .
.
Якщо всі елементи якого-небудь рядка (стовпчика) матриці помножити на деяке число, то і визначник матриці помножиться на це число.
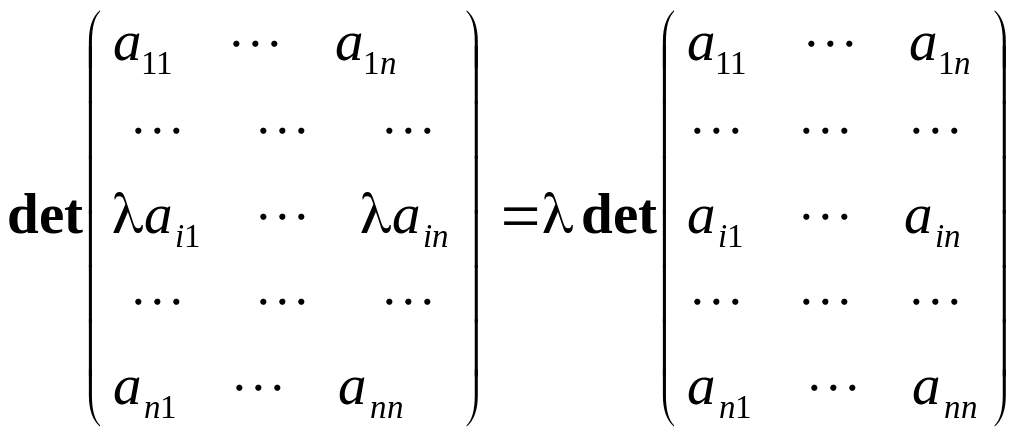
Визначник матриці, рядок (стовпчик) якої є сумою двох рядків(стовпчиків) дорівнює сумі відповідних визначників.
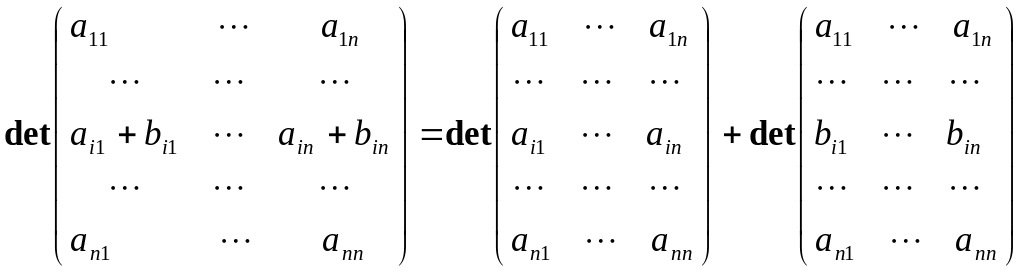
При транспонуванні матриці її визначник не змінюється.
![]() .
.
При перестановці двох довільних рядків (стовпчиків) матриці її визначник змінює знак на протилежний.

Визначник матриці, що містить два однакові рядки (стовпчики), дорівнює нулю.
Якщо до одного з рядків (стовпчиків) матриці додати інший, помножений на деяке число, то визначник матриці не зміниться.
Мінором
![]() елемента
елемента
![]() матриці А будемо називати визначник
матриці, утвореної викреслюванням у
матриці А рядка і стовпчика, де
стоїть цей елемент.
матриці А будемо називати визначник
матриці, утвореної викреслюванням у
матриці А рядка і стовпчика, де
стоїть цей елемент.
Алгебричним
доповненням елемента
матриці А будемо називати число
![]() .
.
Визначник матриці дорівнює сумі добутків елементів будь-якого рядка (стовпчика) матриці на їх алгебричні доповнення.
![]() .
.
Остання властивість дозволяє обчислювати визначники квадратних матриць будь-якого порядку, зведенням до обчислення визначників на одиницю меншого порядку. Наприклад,
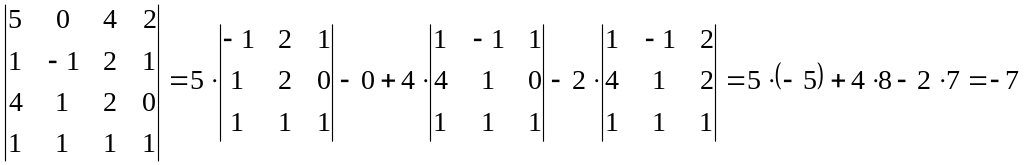 .
.
Рангом
матриці будемо називати найвищий
порядок відмінного від нуля мінора цієї
матриці. Наприклад, ранг матриці
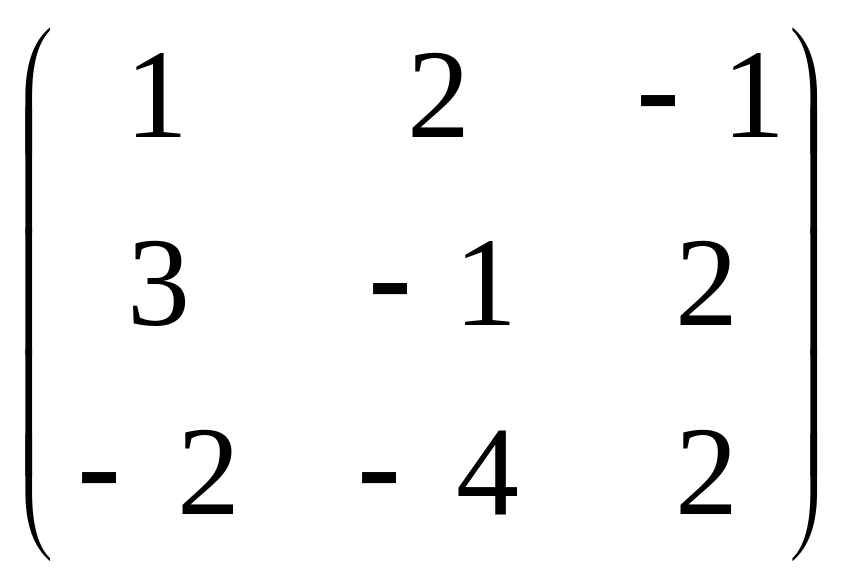 дорівнює 2, бо мінор третього порядку
дорівнює 2, бо мінор третього порядку
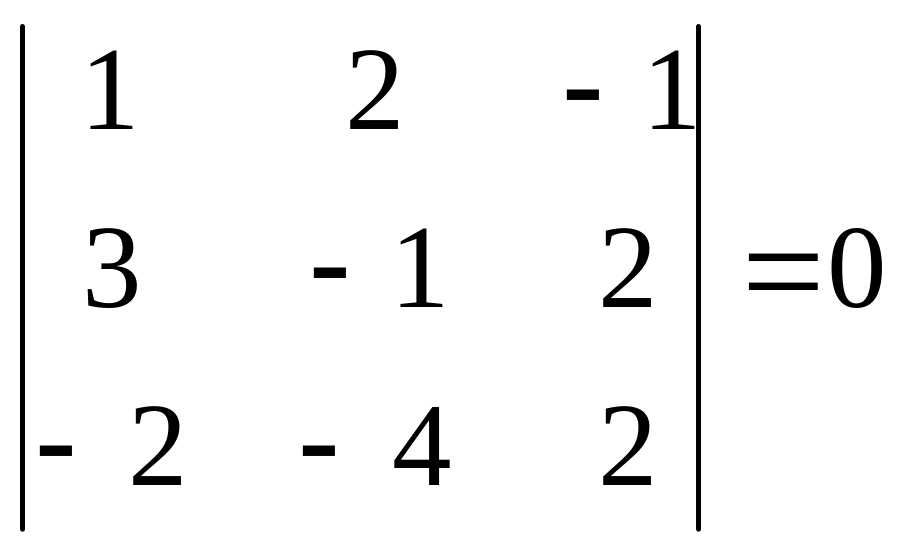 ,
а мінор другого порядку
,
а мінор другого порядку
![]() .
.
Квадратна
матриця
![]() називається оберненою до матриці
називається оберненою до матриці
![]() ,
якщо
,
якщо
![]() .
.
Матриця
називається невиродженою, якщо
![]() .
Кожна невироджена матриця має обернену.
Обернена матриця обчислюється за
формулою
.
Кожна невироджена матриця має обернену.
Обернена матриця обчислюється за
формулою
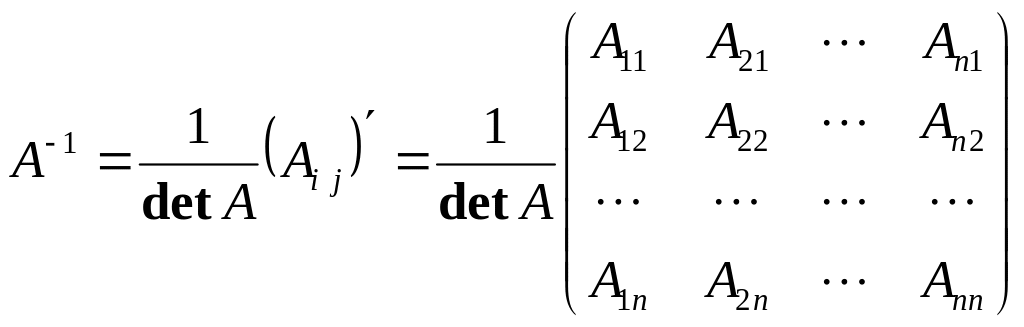 .
.
Тут
![]() —
алгебричне доповнення елемента
—
алгебричне доповнення елемента
![]() матриці
.
матриці
.
Приклад
1. Знайти
матрицю, обернену до матриці
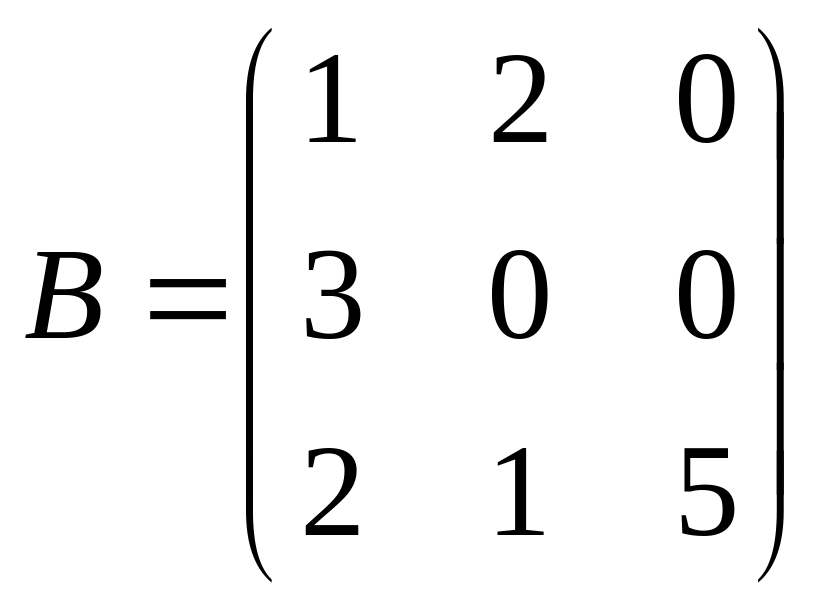 .
.
Розв’язання:
![]() .
Знаходимо алгебричні доповнення
елементів матриці
.
Знаходимо алгебричні доповнення
елементів матриці
![]() .
.
![]()
![]()
![]()
![]()
![]() Тоді,
Тоді,
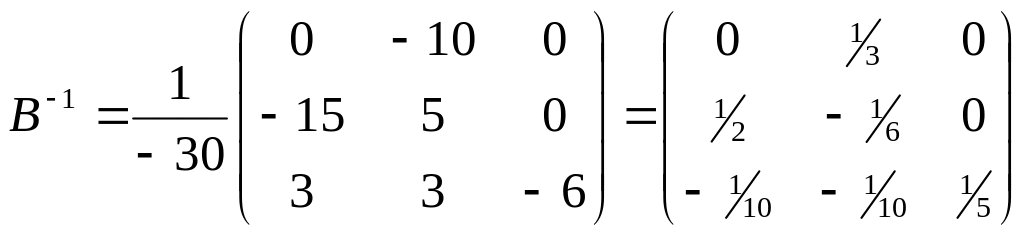 .
.
