2.5 Обработка прямых измерений с многократными наблюдениями

Рассмотрим группу из N независимых результатов наблюдений случайной величины x и определим последовательность ее обработки. Правила обработки результатов измерения с многократными на­блюдениями учитывают следующие факторы:

– обрабатывается ограниченная группа из n наблюдений;

– результаты наблюдений могут содержать систематическую по­грешность;

– в группе наблюдений могут встречаться грубые погрешности;

– распределение случайных погрешностей может отличаться от нормального.

Обработка результатов наблюдений производится в следующей по­с­ле­д­о­в­а­тельности [12]:

1. Исключить известные систематические погрешности из результа­тов наб­лю­дений (введением поправки).

2. Вычислить среднее арифметическое исправленных результатов на­бл­юд­е­ний, принимаемое за результат измерения:

.

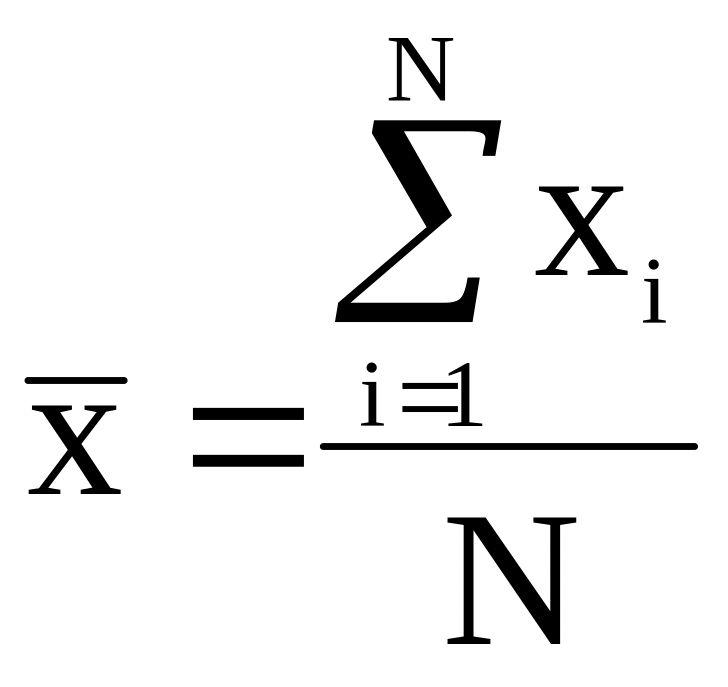3. Вычислить оценку среднего квадратического отклонения резуль­татов наблюдения

.

Вычислив оценку СКО результата наблюдений, целесообразно проверить наличие в группе наблюдений грубых погрешностей (при нормальном законе распределения ни одна случайная по­грешность, с вероятностью практически равной единице, не может выйти за пределы ). Наблюдения, содержащие грубые по­грешности, исключают из группы и заново повторяют вычисления и .

4. Вычислить оценку СКО результата измерения по формуле

.

4. Проверить гипотезу о том, что результаты наблюдений принадле­жат нормальному распределению.

При числе наблюдений n<15 принадлежность их к нормальному рас­пределению не проверяют, а доверительные границы случайной погрешно­сти результата определяют лишь в том случае, если достоверно известно, что результаты наблюдений принадлежат нормальному закону.

4. Вычислить доверительные границы Δ_г случайной погрешности ре­зультата измерения при заданной вероятности Р_д:

Δ_г = ,

где t_p – коэффициент Стьюдента.

7. Вычислить границы суммарной неисключенной систематической по­грешности (НСП) результата измерений [12].

Неисключенная систематическая погрешность результата образуется из неисключенных систематических погрешностей метода, средств изме­рений, погрешностей поправок и др.

При суммировании эти составляющие рассматриваются как случайные величины. При отсутствии данных о виде распределения неисключенных составляющих систематических погрешностей их распределения принимают за равномерные. При равномерном распределении неисключенных система­тических погрешностей границы неисключенной систематической погреш­ности результата измерения вычисляют по формуле

,

где – граница i-й неисключенной составляющей систематической по­грешности; k – коэффициент, определяемый принятой доверительной вероятностью (при Р_д=0,95 k=1,1); m – количество неисключенных составляющих.

Доверительную вероятность для вычисления границ НСП принима­ют той же, что при вычислении границ случайной погрешности резуль­тата измерения.

8. Вычислить доверительные границы погрешности результата измерения.

Анализ соотношения между неисключенной систематической погрешностью и случайной погрешностью показывает, что если , то неисключенной систематической погрешностью можно пренебречь и принять границы погрешности результата равными Δ_г. Если , то случайной погрешностью можно пренебречь и принять границы по­грешности результата равными .

Если оба неравенства не выполняются, вычисляют СКО результата как сумму неисключенной систематической погрешности и случайной составляющей:

.

Границы погрешности результата измерения в этом случае вычисляют по формуле . Коэффициент К в данном случае вычисляют по эмпирической формуле

.

При симметричном доверительном интервале погрешности резуль­тат измерения представляют в форме , Р_д.

При отсутствии данных о видах функции распределения состав­ляющих погрешности результата или при необходимости дальнейшей обработки результатов результат измерения представляют в форме , , N, .