
- •Основы измерений в технике связи и стандартизации
- •Введение
- •1. Основные понятия метрологии Измерение, физическая величина, метод измерения, средства измерений, измерительный сигнал, характеристики измерительных сигналов, характеристики средств измерений
- •1.1 Основные метрологические термины
- •1.2 Классификация измерений
- •1.3 Средства измерения электрических величин
- •1.4 Характеристики средств измерений
- •1.5 Измерительная информация и ее характеристики
- •1.6 Эталоны единиц электрических величин
- •2.1 Классификация погрешностей измерений
- •2.2 Математическое описание случайных погрешностей
- •2.3 Доверительный интервал и доверительная вероятность
- •2.4 Нормирование метрологических характеристик средств измерений
- •2.5 Обработка прямых измерений с многократными наблюдениями
- •2.6 Оценка погрешностей косвенных измерений
- •2.7 Правила суммирования случайных и систематических погрешностей
- •2.8 Контроль и достоверность контроля
- •3.2 Измерительные генераторы
- •3.3 Анализаторы спектра
- •3.4 Измерители нелинейных искажений
- •4.1 Общие сведения
- •4.2 Источники погрешности цифровых измерительных приборов
- •4.3 Цифровые осциллографы
- •4.4 Цифровые частотомеры
- •4.5 Цифровые измерители сдвига фаз
- •4.6 Цифровые измерители емкости и сопротивления
- •4.7 Цифровые измерительные генераторы низких частот
- •4.8 Цифровые вольтметры
- •4.9 Цифровые ваттметры
- •4.10 Виртуальные приборы
- •5 Основы квалиметрии Показатель качества, методы определения показателей качества, объект стандартизации, стандарт, сертификация соответствия, схема сертификации
- •5.1 Измерение и оценивание качества
- •5.2 Государственная система стандартизации
- •5.3 Организация системы сертификации гост
- •Библиографический список
2.2 Математическое описание случайных погрешностей
Случайные погрешности проявляются при многократных и равноточных измерениях, т.е. при измерениях, выполненных по одной и той же методике, средствах измерений одинаковой точности и при неизменных внешних условиях. Аналитически случайные погрешности измерений описываются и оцениваются с помощью аппарата теории вероятности и математической статистики.
Каждая случайная погрешность возникает вследствие одновременного воздействия на результат наблюдения многих возмущающих факторов. В этом случае предсказать результат отдельного наблюдения и исправить его введением поправки невозможно. Можно лишь с определенной долей уверенности утверждать, что истинное значение измеряемой величины находится в пределах разброса результатов наблюдений от xmin до xmax, где xmin и xmax – соответственно, нижняя и верхняя границы разброса
Случайные
погрешности i-го
результата измерения
![]() можно представить в виде разности
можно представить в виде разности
![]() ,
,
где М[Х] – математическое ожидание измеряемой величины.
Случайные погрешности рассматриваются как случайные величины. Случайная величина – величина, которая может принимать то или иное значение, причем ее значения заранее точно не известны. Случайные величины могут быть дискретными и непрерывными.
Полными и исчерпывающими характеристиками случайных величин являются законы распределения (функция распределения и плотность вероятности). Каждый закон распределения представляет собой некоторую функцию, описывающую величину с вероятностной точки зрения.
Во многих практических случаях бывает достаточно указать только отдельные числовые характеристики, определяющие существенные черты закона распределения.
В табл. 2.1 приведены основные вероятностные и статистические числовые характеристики случайных величин. Рассмотрим числовые характеристики, приведенные в таблице более подробно.
Положение распределения на числовой оси характеризует математическое ожидание случайной величины. Можно сказать, что математическое ожидание указывает некоторое среднее, ориентировочное значение, около которого группируются все возможные значения случайной величины.
Дисперсия случайной величины – это характеристика рассеивания (разбросанности) случайной величины относительно ее математического ожидания. Оценка дисперсии и дисперсия выражается в единицах измерения случайной величины в квадрате. Среднее квадратическое отклонение и оценка среднего квадратического отклонения выражается в единицах измерения случайной величины.
Таблица 2.1
Вероятностные характеристики |
Статистические характеристики (оценки) |
Математическое ожидание дискретной случайной величины:
Математическое ожидание непрерывной случайной величины:
|
Оценка математического ожидания (статистическое среднее или выборочное среднее):
|
Дисперсия дискретной случайной величины:
Дисперсия непрерывной случайной величины:
|
Оценка дисперсии:
Несмещенная оценка дисперсии:
|
Среднее квадратическое отклонение:
|
Оценка
среднего квадратического отклонения:
|
Начальный момент k-го порядка дискретной случайной величины:
Начальный момент k-го порядка непрерывной случайной величины:
|
Оценка начального момента k-го порядка:
|
Центральный момент k-го порядка дискретной случайной величины:
Центральный момент k-го порядка непрерывной случайной величины:
|
Оценка центрального момента k-го порядка:
|
Для более подробного описания распределения применяются моменты высших порядков. Третий центральный момент служит для характеристики асимметрии распределения и имеет размерность куба случайной величины. Безразмерной оценкой асимметрии является коэффициент асимметрии:
![]()
Четвертый центральный момент служит для характеристики крутизны спадов распределения (иногда используется термин «островершинность распределения»). Крутизну спадов можно оценить с помощью эксцесса случайной величины. Эксцессом случайной величины называется величина
![]()
Число
3 вычитается из отношения
![]() потому, что для нормального закона
распределения
потому, что для нормального закона
распределения
![]() .
Таким образом, для нормального
распределения эксцесс равен нулю.
Кривые, более островершинные по сравнению
с нормальной, обладают положительным
эксцессом. Более плосковершинные кривые
– отрицательным эксцессом.
.
Таким образом, для нормального
распределения эксцесс равен нулю.
Кривые, более островершинные по сравнению
с нормальной, обладают положительным
эксцессом. Более плосковершинные кривые
– отрицательным эксцессом.

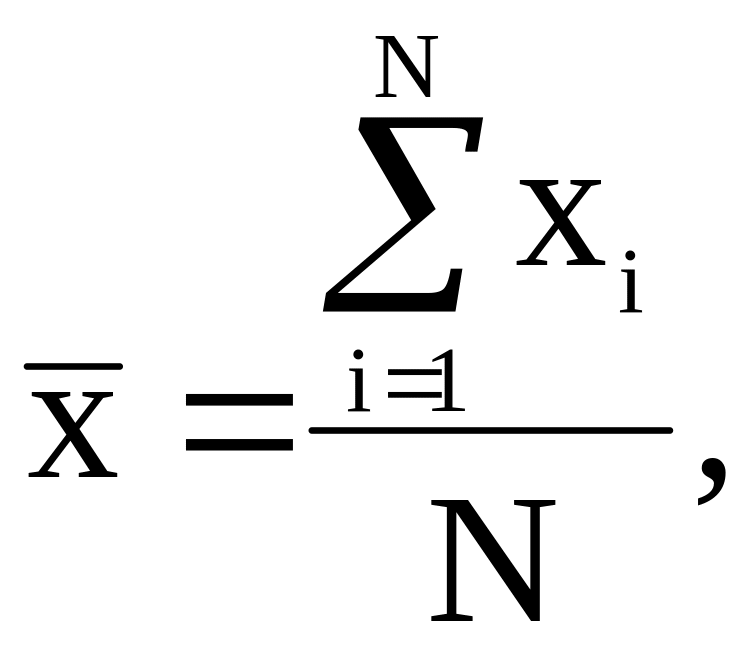 где
N
– количество измерений
где
N
– количество измерений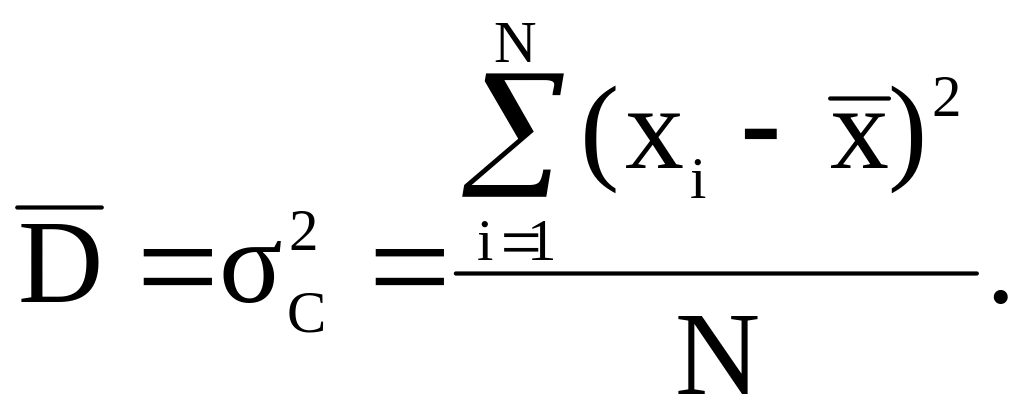
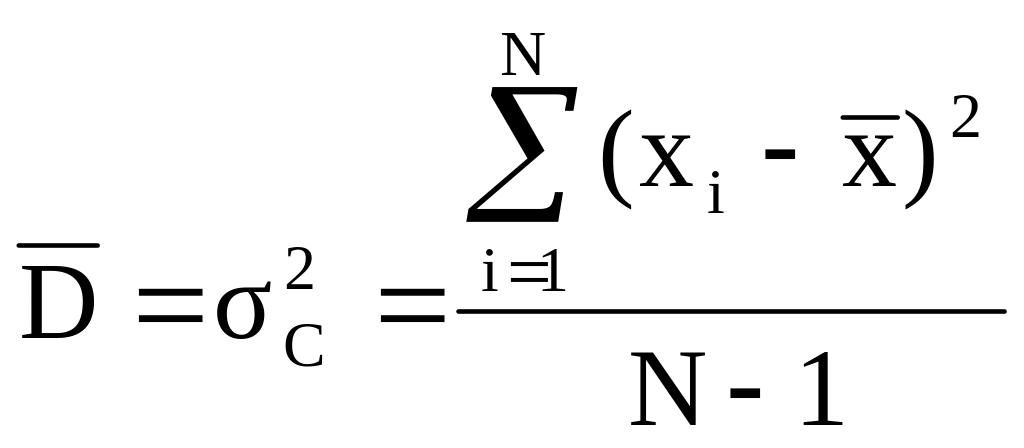
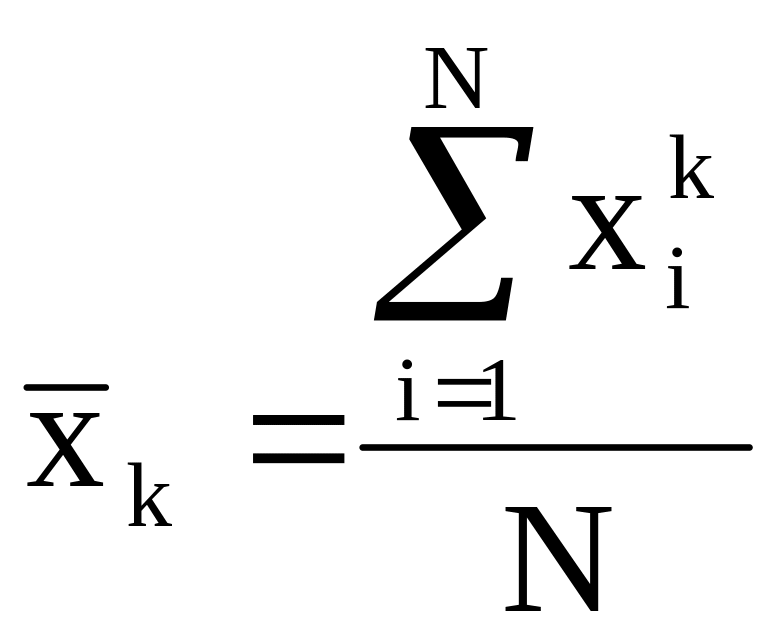
 где
где