Глава 14. Вариационные интегральные принципы классической механики

14.1. Общие понятия

Вариационными принципами классической механики называют общие закономерности механического движения, позволяющие из совокупности кинематически возможных движений механической системы, т. е. движений, допускаемых наложенными на систему связями, выделить действительное движение, которое она будет со­вершать в заданном силовом поле.

Вариационные принципы разделяются на дифференциальные и интегральные. Дифференциальные вариационные принципы дают кри­терий истинного движения, отнесенный к некоторому моменту времени, а интегральные — к конечному интервалу времени.

Важнейшим и наиболее общим дифференциальным вариационным принципом классической механики является принцип возможных перемещений.

Важнейшими интегральными принципами классической механики являются принцип Гамильтона — Остроградского и принцип стационарного действия Мопертюи — Лагранжа.

Положение голономной механической системы с s степенями свободы относительно системы отсчета определяется s обобщенными координатами ( ), которые при движении механической системы изменяются, являясь функциями времени t.

Совокупность обобщенных координат механической системы ( ) для каждого момента времени можно рассматривать как координаты точки в пространстве s измерений. Тогда каждой конфигурации механической системы, т. е. ее положению в прост­ранстве, будет соответствовать определенная точка в s-мерном пространстве. Условимся называть s-мерное пространство прост­ранством конфигураций.

С течением времени положение системы в пространстве изме­няется и точка, изображающая эту систему, описывает в прост­ранстве конфигураций некоторую кривую. Условимся называть эту кривую траекторией движения системы. Движение изображающей точки вдоль этой траектории отображает действительное движе­ние системы в пространстве.

Очевидно, что каждой точке такой траектории и пространстве конфигураций соответствует определенное положение механической системы в реальном евклидовом пространстве.

Отбор действительного движения механической системы из сово­купности ее возможных движений можно осуществить при помощи анализа ее движения в пространстве конфигураций на основе инте­гральных вариационных принципов, изложенных ниже.

14.2. Дифференцирование и варьирование в механике

Предположим, что механическая система имеет одну степень свободы и ее положение определяется обобщенной координатой . Дифференцируем это равенство по времени

.

Дифференциал обобщенной координаты dq соответствует ее из­менению вследствие изменения времени, т. е. вследствие действительного движения системы.

а) б)

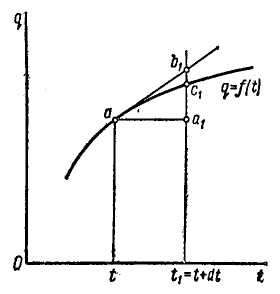
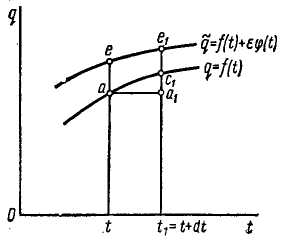
Рис. 3.92

Геометрически dq есть отрезок (рис. 3.92, а); но с точностью до бесконечно малых высшего порядка dq равен отрез­ку . Дадим функции , при заданном зафиксированном значении ар­гумента t, произвольное приращение

,

где — есть произвольно малое постоян­ное число, а — произвольная диф­ференцируемая функция времени.

Получим семейство новых функций времени

.

Графически одна из функций представлена новой кривой, бесконечно близкой к кривой функции q (рис. 3.92, б).

Произвольное изменение функции , являющееся следствием не изменения аргумента, а изменения вида самой функции, называется синхронной вариацией функции

.

Вариация функции в момент t (рис. 3.92, б) соответствует от­резку ае.

Рассмотренная операция варьирования функции называется син­хронным варьированием.

Сопоставляя операции дифференцирования и варьирования функ­ции, устанавливаем, что дифференциал dq является изменением ординаты q вдоль кривой , а вариация функции dq опреде­ляет изменение q при фиксированном t, связанное с переходом от данной кривой к другой смежной с ней кривой .

Операции дифференцирования и варьирования, являющиеся незави­симыми друг от друга операциями, обладают свойством коммута­тивности в последовательности их применения.

Укажем также, что вариация определенного интеграла с постоян­ными пределами интегрирования равна определенному интегралу от вариации подынтегральной функции

.

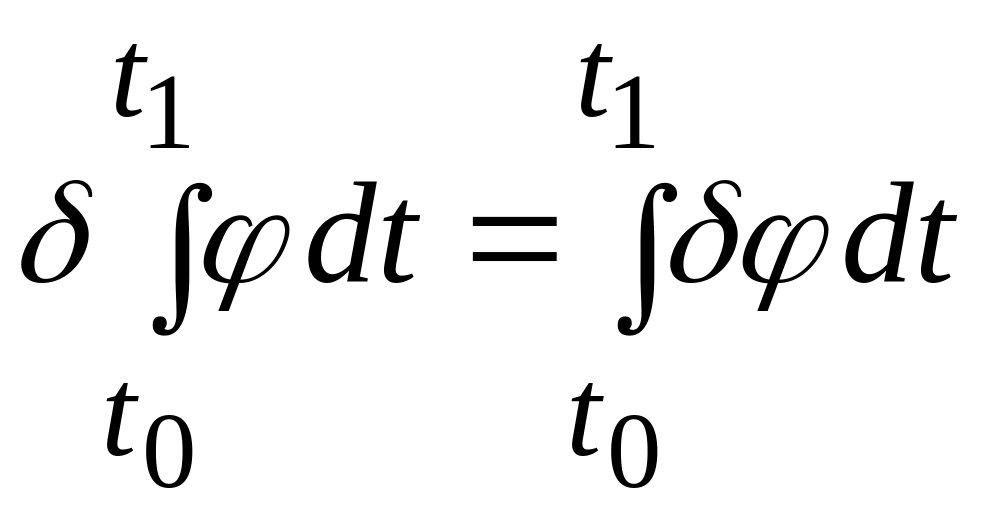Основываясь на том, что операции синхронного варьирования и дифференцирования по времени являются независимыми друг от друга операциями и обладают свойствами коммутативности в после­довательности их применения, а также, используя интегрироваие по частям, рассмотрим следующее преобразование, встречающееся в дальнейшем:

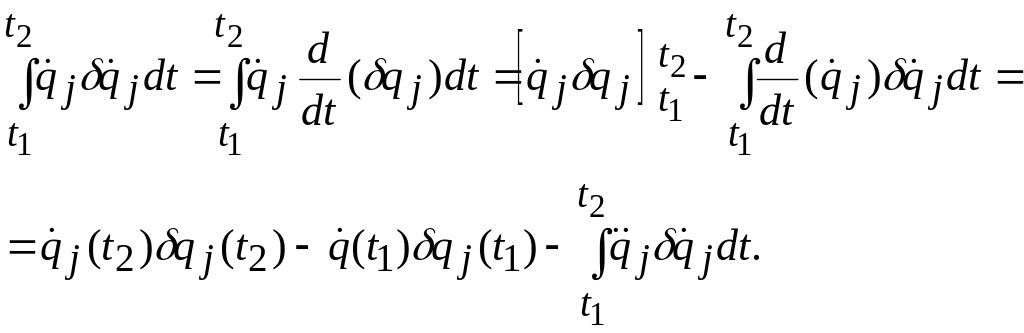
При имеем

.

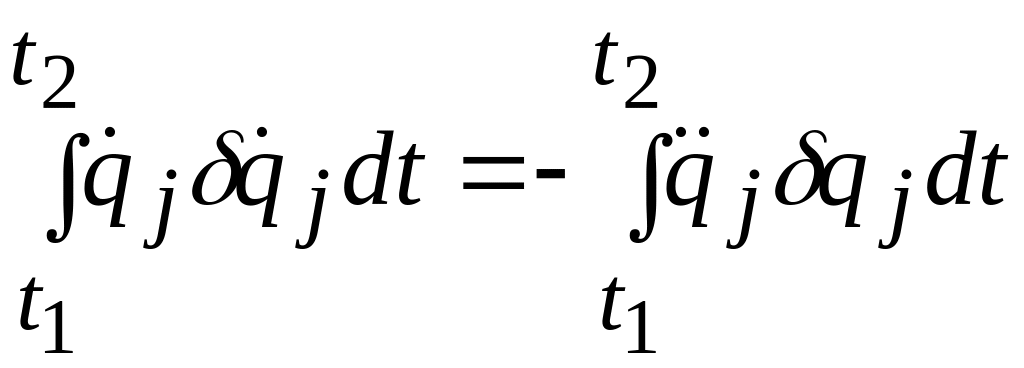Рассмотрим теперь полную вариацию функции .

Полной или асинхронной вариацией называют изменение функции, вызванное как изменением вида функции, так и изменением аргумента.

Примем изменение аргумента t равным , где —функция с не равной нулю производной по времени. Тогда измененный аргумент

.

Определим полную вариацию функции

.

Так как при :

,

а

,

то

. (3.32)

На рис. 3.94 полная вариация изображена отрезком

,

где

,

т.е.

.

Из равенства (3.32) видно, что изменение функции состоит из двух частей: 1) синхронной вариации и 2) — изменения функции вследствие изменения аргумента t на величину .

Полная вариация и дифференцирование свойством коммутативности не обладают.

Формулу для полной вариации от определенного интеграла можно представить в следующем виде:

.

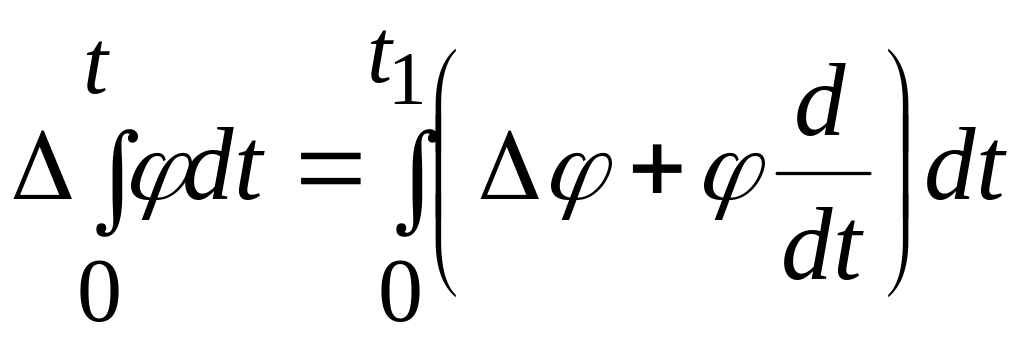В приложениях к движению варьирование связано с рассмотрением движения механической системы по кривой, являющейся действительной траекторией механической системы в пространстве конфигураций, и по допустимым кривым или кривым сравнения.

Действительная траектория механической системы в пространстве конфигураций соответствует действительному движению механической системы под влиянием приложенных сил и заданных начальных условий.

Кривая сравнения соответствует движению, бесконечно близкому к действительному, допускаемому существующими связями.