Література

1. Основы геофизических методов разведки \ Толстой М.И. и др. – К.: Вища школа. Головное издательство, 1985. – 327 с.

Лабораторна робота № 3.2

РІШЕННЯ ПРЯМОЇ ТА ОБЕРНЕНОЇ ЗАДАЧІ МАГНІТОРОЗВІДКИ ДЛЯ ТІЛ ПРАВИЛЬНОЇ ГЕОМЕТРИЧНОЇ ФОРМИ

3.2.1 Мета і завдання роботи

Метою роботи є дослiджєння зв`язку мiж джерелами (об`єктами) найпростiшої форми i магнiтними ефектами, якi вони зумовлюють, та рiшення обернених задач.

Завдання роботи: 1 - рішення прямої задачі магнітометрії для тіл правильної геометричної форми; 2 - рішення оберненої задачі методом характерних точок.

У результатi виконання роботи студент повинен знати загальні вирази визначення магнiтних полiв за заданим розподiлом джерела, знати формули визначення аномалiй для елементарних об`єктiв та вмiти користуватись ними, отримати навики рішення оберненої задачі.

3.2.2 Короткi теоретичнi відомості

Рiшенням прямої задачi для тіл правильної геометричної форми є визначення магнiтного ефекту вiд аномальних об`єктiв заданої форми та мiсця розташування вiдносно площини, що ототожнюється з площиною денної поверхнi i є одним з iнструментів кількісних методiв геологiчної iнтерпретацiї магнiтних аномальних полiв.

Пряма задача - знаходження (або розрахунок) аномалії від тіла з відомими формою, розмірами, глибиною залягання та магнітними властивостями. Суть методу заключається у використаннi встановленого зв`язку мiж координатою по профiлю (початок координат в точцi максимального значення аномалiї), що вiдповiдає характерним долям вiд максимального значення аномалiї i координатою глибини залягання цєнтра збурюючого тiла. Пiсля визначення можна оцiнити магнiтний момент збурюючого тiла через максимальне значення видiленої аномалiї.

Обернена задача - за даними розподілу магнітного поля необхідно знайти розміри збуруючого тіла, форму та глибину залягання.

В даній роботі розглянемо розв`язок прямої та оберненої задачі для вертикального стержня (магнітний однополюс) і однорідної вертикально намагніченої кулі.

Вертикальний стержень. Пряма задача. Розглянемо вертикальний тонкий стержень, що безкінечно простягується на глибину, тобто один магнітний полюс знаходиться у верхній частині стержня, а нижній залягає настільки глибоко, що його впливом можна знехтувати. Магнітний потенціал в довільній точці P(x,z) (див. рис. 3.3)

Рисунок 3.3 - Графіки Z і H над вертикальним стержнем

буде мати вигляд: , (3.6)

де ;

h - глибина залягання магнітного полюса;

m - магнітна маса.

Модуль повного вектора напруженості магнітного поля буде

. (3.7)

Вертикальна складова Z магнітного поля запишеться у вигляді

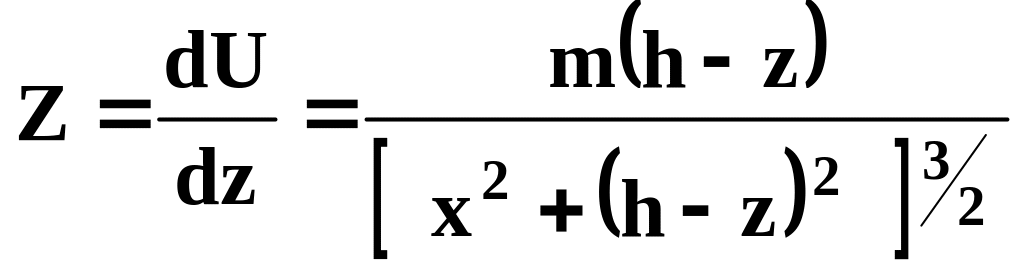. (3.8)

Горизонтальна складова H

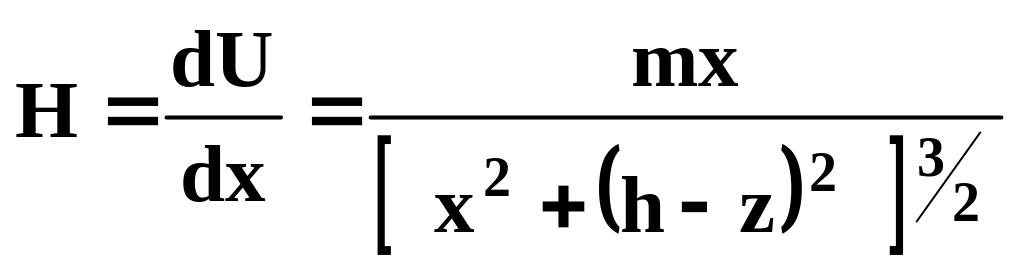. (3.9)

При x=0 T і Z приймають максимальне значення, тобто

. (3.10)

Якщо то T і Z прямують до нуля з різних сторін.

Горизонтальна складова змінюється зовсім по іншому. При x=0 складова H=0. При H прямує до нуля. Щоб знайти екстремальні точки, необхідно похідну прирівняти до нуля:

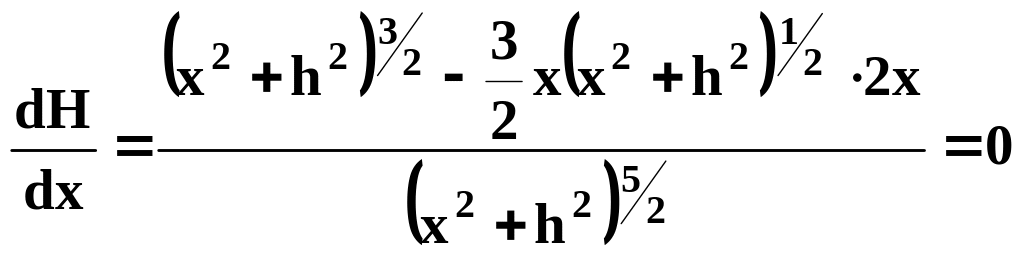(3.11)

Після деяких перетворень одержимо

. (3.12)

Звідси . (3.13)

Підставивши (3.13) в (3.9) одержимо:

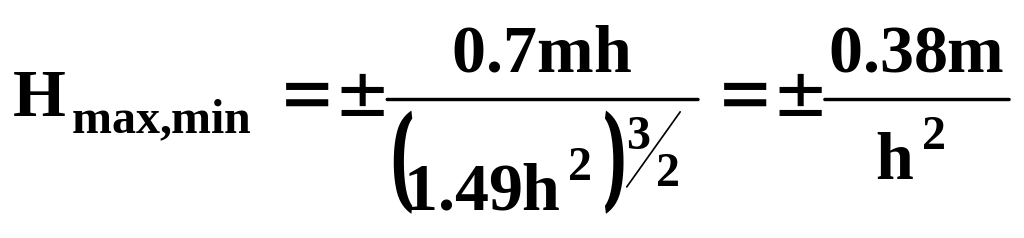. (3.14)

Відношення . (3.15)

Обернена задача. Для розв`язання оберненої задачі використаємо два рівняння:

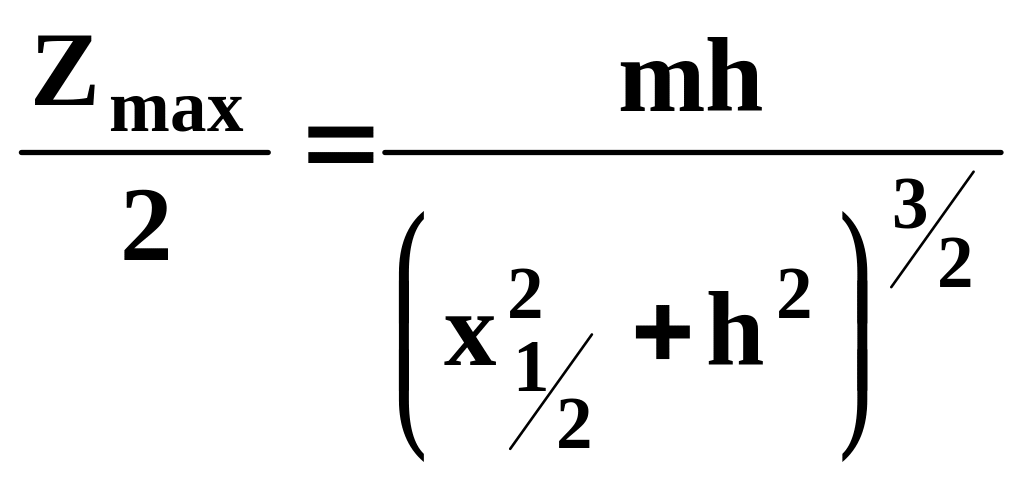та . (3.16)

Підставивши одне рівняння в друге, одержимо:

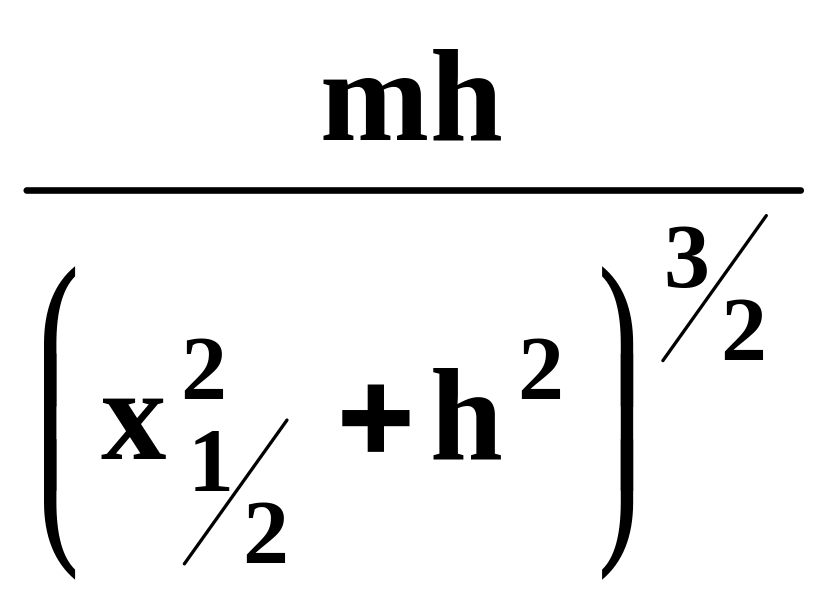. (3.17)

звідси h = 1,305x . (3.18)

Масу полюса можна знайти за формулою:

. (3.19)

Використовуючи горизонтальну складову, глибину можна визначити за формулою: h= 1,4x , (3.20)

а масу полюса за виразом:

. (3.21)

Вертикально намагнічена куля (диполь). Диполь складається з двох точкових магнiтних полюсiв, якi розташованi близько один вiд одного (рис. 3.4).

Рисунок 3.4 - Графіки Z і H над вертикально намагніченою кулею

Розмістимо центр кулі на вісі z на глибині h. Тоді в довільній точці P на поверхні потенціал вертикальної і горизонтальної складової аналогічно з гравітаційним буде:

, , (3.22)

де V - потенціал притягання;

G - гравітаційна стала;

- щільність порід.

Для гравітаційного притягання однорідної кулі

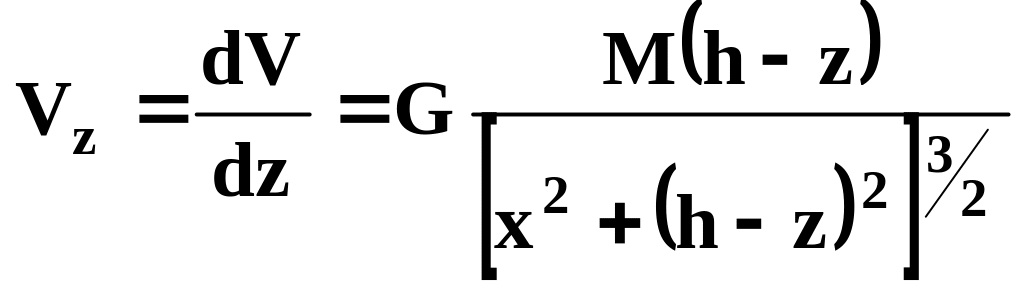. (3.23)

З врахуванням (3.23), формулу (3.22) можна записати у вигляді

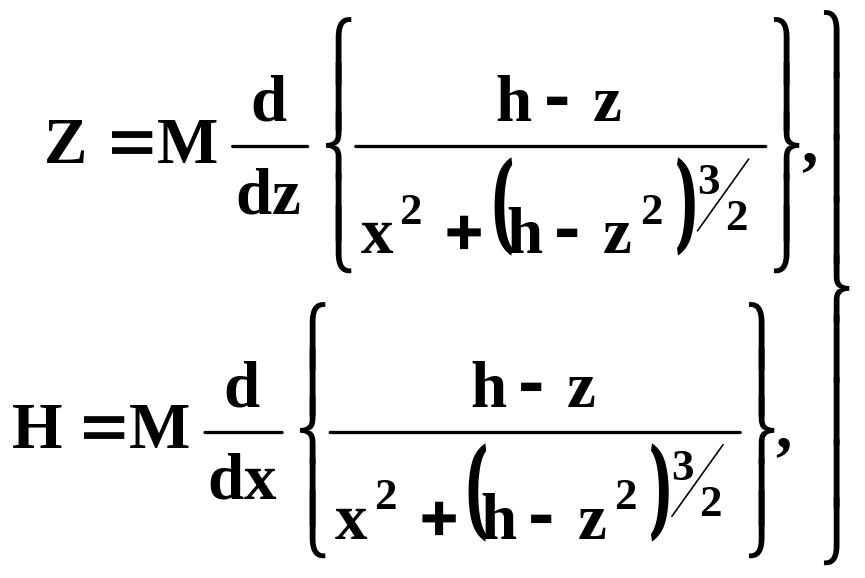(3.24)

де M - магнітний момент кулі: M = JV;

J - інтенсивність намагнічування;

V - об`єм кулі: ;

R - радіус кулі.

Виконавши диференціювання (3.24) і деякі перетворення, одержимо:

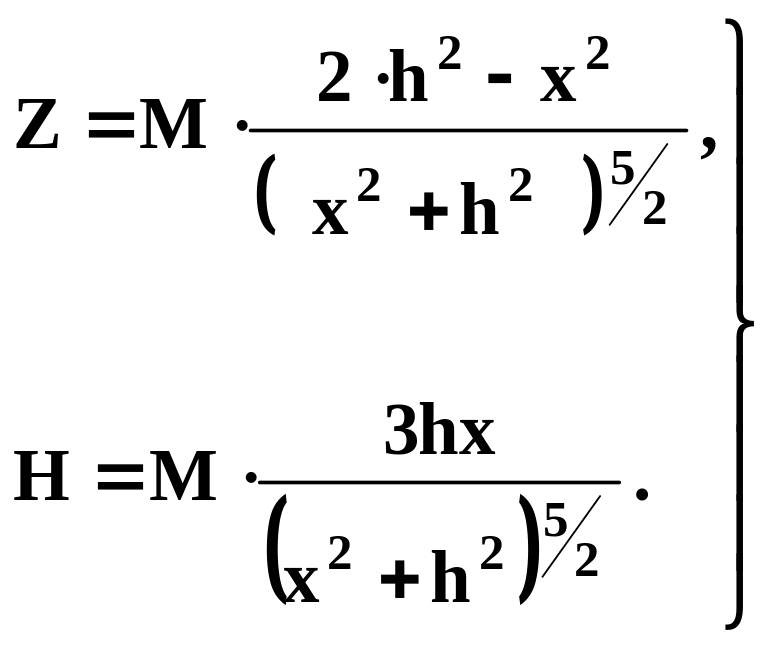(3.25)

Максимальне значення буде в точці при x=0, тобто

. (3.26)

Вертикальна складова Z=0 в точках, коли , тобто

. (3.27)

Z екстремальне знаходиться з виразу . В цьому випадку

. (3.28)

Горизонтальна складова H в точці x=0 також дорівнює нулю. При H прямує до нуля. H і H в точках, коли , тобто

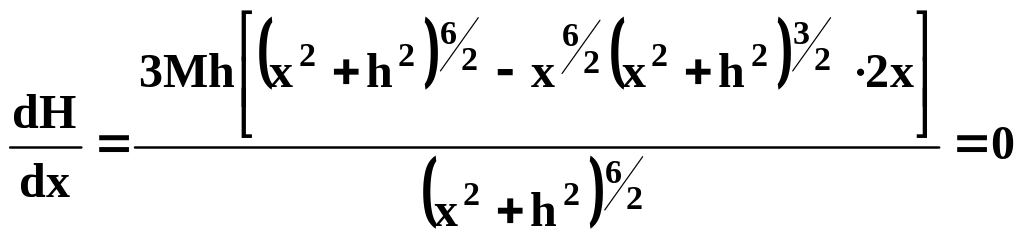. (3.29)

Після нескладних перетворень, одержимо: .

Звідси. . (3.30)

Підставивши (3.30) в другу рівність (3.24), одержимо екстремальні значення:

. (3.31)

З формул (3.26) та (3.31) .

Обернена задача для кулі. По графіку Z глибину залягання

кулі знаходять по абсцисі точок x , де Z=0. З формули (3.27)

. (3.32)

При відомій глибині h не важко знайти магнітний момент кулі:

. (3.33)

Задача знаходження радіуса кулі має неоднозначне рішення, оскільки R зв`язано з магнітним моментом і інтенсивністю намагнічування одним рівнянням. Радіус кулі можна знайти, знаючи повне значення вертикальної складової Z і магнітну сприйнятливість для кулі:

. (3.34)

По графіку H глибина кулі визначається з формули (3.30)

. (3.35)

Знаючи глибину, з формули (3.31) знаходять магнітний момент:

. (3.36)

3.2.3 Завдання роботи

Розрахувати магнiтне поле над кулею та вертикальним стержнем.

Розрахунки провести по профiлю (x =0) в точках (в м.), де n = 0, 1, 2, 4, 8, 10, 20, 40, 50, 100.

1) параметри вертикального стержня:

h = 200 м;

m = ;

кг/м ;

2) параметри кулi:

м; n - задає викладач.

h = 250 м;

A/м;

3.2.4 Запитання для самоперевірки

1. У чому суть прямої задачі магніторозвідки?

2. У чому суть оберненої задачі магніторозвідки?

3. Запишіть формулу визначення вертикальної складової Z для вертикального стержня.

4. За якою формулою можна визначити глибину залягання вертикального стержня?

5. Чим відрізняються графіки вертикальної складової для кулі і вертикального стержня?

6. Перечисліть характерні точки для складових Z і H над кулею.

7. За якою формулою можна визначити глибину залягання центра кулі.

3.2.5 Форма звітності

1. Навести графіки Z і H.

2. Проаналізувати графіки шляхом їх порівняння між собою.

3. Привести дані рішення оберненої задачі.

4. Оцінити точність рішення оберненої задачі.

Література

1. Основы геофизических методов разведки \ Толстой М.И. и др. – К.: Вища школа. Головное издательство, 1985. – 327 с.