Метод простих ітерацій
Будемо використовувати позначення попередньої лекції. Зокрема, ми будемо розглядати систему лінійних алгебраїчних рівнянь (1.3.1), яку можна записувати й у матричному виді, згаданому в попередній лекції:
(3.1.1)
.
Нагадаємо, що тут А - матриця системи, B - стовпець вільних членів, а X - стовпець невідомих. У попередній лекції мова йшла про таке рішення системи (3.1.1), що з математичної точки зору є точним. У дійсності жоден комп'ютер не маніпулює з точними числами - там числа наближені; тому й при методі Гаусса, і при методі Крамера, і при методі жордановых виключень у дійсності комп'ютер видасть не точний, а наближена відповідь, хоча в самих цих методів «погрішність методу» дорівнює нулю.
Існують, однак, методи рішення системи (3.1.1), які по самій своїй природі дають не точний, а наближена відповідь. Найвідомішим з таких методів є метод простих ітерацій. От його опис.
Перетворимо систему (3.1.1) до іншого виду, виражаючи всі невідомі через самих себе, -
(3.1.2)
де
- нові числові матриці, а Х
- колишній
стовпець невідомих. Перехід від (3.1.1)
до (3.1.2) можна зробити багатьма способами.
От приклад: є система
;
з
першого рівняння одержимо
із другого рівняння
отже, при такому перетворенні
Нехай
стовпцю невідомих Х
довільним образом приписане конкретне
числове значення
Тоді виникає можливість за допомогою
матричної рівності (3.1.2) побудувати
рекурентно стовпці
,
де k=2,3,4,...
. Виявляється, що при деяких умовах на
D
стовпці
«наближаються
як завгодно близько»
до рішення системи (3.1.1). Дія по обчисленню
за допомогою
називається ітерацією;
звідси – метод
ітерацій.
Уведемо нові терміни для точного вираження останнього твердження.
Нехай
- стовпець із n
чисел, записаний заради економії місця
у вигляді рядка, заданий для кожного
k=1,2,3,...
. Нехай, далі, є стовпець
Назвемо відстанню
від
до
число
ясно,
що
- числова послідовність; якщо ця числова
послідовність прагне до нуля, то говорять,
що стовпці
прагнуть
до стовпця
Z
або
що Z
є межею послідовності
.
Таким чином, метод ітерацій рішення системи лінійних алгебраїчних рівнянь складається в побудові послідовності , що має своєю межею стовпець-рішення.
Основне в організації процесу ітерацій - створити таку матрицю D, щоб послідовність стовпців сходилася до рішення. Сформулюємо дві умови, при виконанні кожного з яких процес ітерацій сходиться:
(1)
якщо
,
те процес ітерацій сходиться до рішення
системи (3.1.1);
(2)
якщо
,
те процес ітерацій сходиться до рішення
системи (3.1.1).
Метод Зейделя
Як і раніше розглядається питання про рішення системи (3.1.1). У попередньому пункті
був
описаний метод простих ітерацій для
рішення такої системи. Суть методу
полягала в тому, що від системи (3.1.1)
треба перейти до системи (3.1.2), а потім
організувати процес ітерацій
.
Метод Зейделя полягає в тому, що ітерації
здійснюються трохи інакше. А саме,
розпишемо рівність
у вигляді звичайних числових рівностей:
згідно
із цими рівностями, числа
відшукуються через числа
Зейдель запропонував відшукувати
по
,
використовуючи ті ж самі формули. Іншими
словами, в ітераціях по Зейделю
враховуються вже знайдені значення
наближень. Сформулюємо остаточно метод
Зейделя: послідовність ітерацій
будується по формулах:
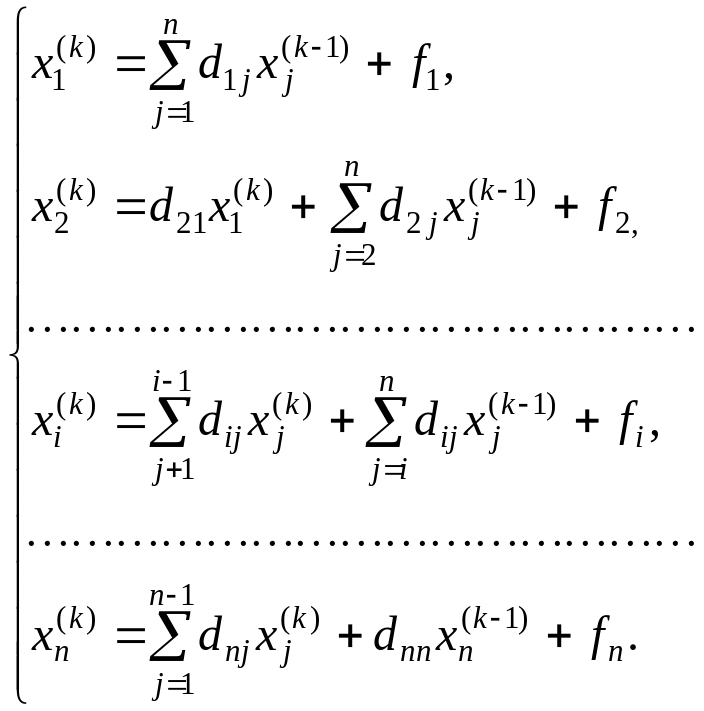
Питання про збіжність процесу ітерацій до рішення вирішується тут так само, як і вище у випадку простих ітерацій: все залежить від матриці D. Умови тут ті ж, що й вище.