1.3. Системи лінійних алгебраїчних рівнянь

Нагадаємо кілька визначень.

Система лінійних алгебраїчних рівнянь – це система рівнянь виду:

(1.3.1)

Тут – невідомі, а – задані коефіцієнти, які прийнятий записувати у вигляді матриць:

, .

Дуже часто в обговоренні таких систем рівнянь використовують матрицю

,

яку називають розширеною матрицею системи; матриця А називається матрицею системи, а матриця B матрицею вільних членів.

Розв'язання системи (1.3.1) - це такий набір чисел , що при підстановці , i=1,2,...,n, всі рівності в (1.3.1) стають тотожностями.

Система (1.3.1) називається спільною, якщо в неї є хоч одне розв'язання, і неспільною, якщо жодного розв'язання в неї немає.

Система (1.3.1) називається визначеною, якщо в неї є розв'язання й притім тільки одне.

Лекция 2

РОЗКЛАДАННЯ В РЯД ТЕЙЛОРА. ВИКОРИСТАННЯ СТЕПЕНЕВИХ РЯДІВ. ПОЛІНОМИ ЧЕБИШЕВА. ЗАСТОСУВАННЯ ЖОРДАНОВИХ ВИНЯТКІВ ДО РОЗВ'ЯЗАННЯ СИСТЕМ ЛІНІЙНИХ АЛГЕБРАЇЧНИХ РІВНЯНЬ И ДО ОБЧИСЛЕННЯ ЗВОРОТНОЇ МАТРИЦІ

2.1. Апроксимація функції по Фур'є.

Нехай функція задана в інтервалі . У цьому випадку (при наявності в неї відповідних властивостей інтегруемості) можна побудувати ряд Фур'є цієї функції, а саме об'єкт

(2.1.1) ,

де

(2.1.2) .

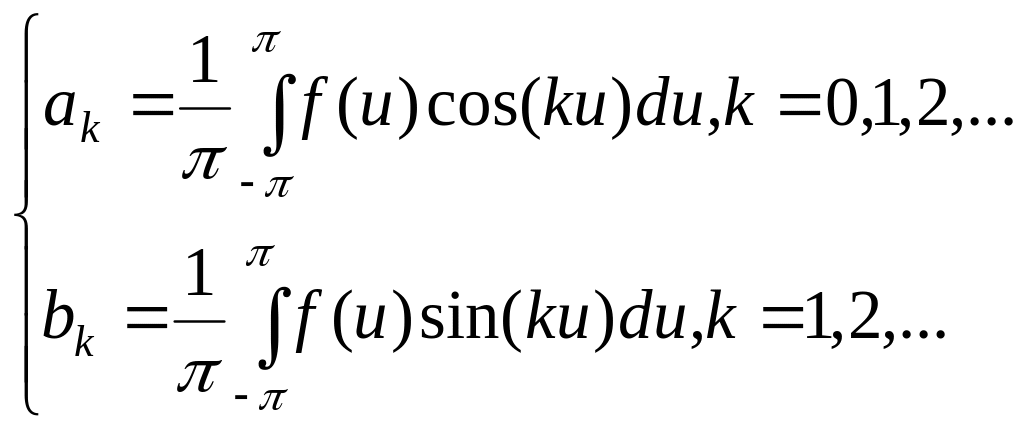Відомо, що для безперервної функції цей ряд сходиться в кожній крапці інтервалу й притім - до значення в цій точці функції . Якщо підсумовування в ряді Фур'є перервати на якімсь доданку, то виникне наближена рівність

,

яке тим точніше, чим більше число доданків у сумі. У цьому й складається апроксимація функції по Фур'є.

Практично організація розрахунків при апроксимації відбувається так: задається той ступінь точності e, з якої треба наблизити число за допомогою часткових сум ряду (2.1.1); потім обчислюють, поступово нарощуючи кількість доданків, часткові суми ряду (2.1.1) і роблять це доти, поки два рази підряд не вийде при підсумовуванні те саме з точністю e число; його й приймають за потрібне наближення. Природно, що при обчисленні часткових сум ряду (2.1.1) потрібні коефіцієнти , які обчислюються за допомогою чисельного інтегрування через визначальні рівності (2.1.2).

Описана ситуація узагальнюється на випадок функції , заданої не на інтервалі , а на довільному інтервалі . У цьому випадку (для безперервної функції ) має місце рівність

(2.1.3)

усередині інтервалу , де

(2.1.4)

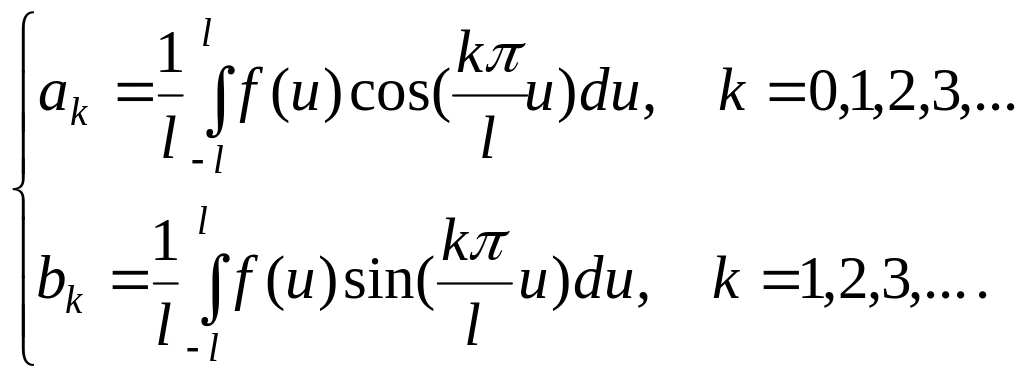
Прийнято виділяти випадки парної й непарної функції, тому що при цьому вираження (21.3) і (2.1.4) істотно спрощуються, а саме:

якщо на інтервалі функція парна, то для всіх мають місце рівності й

(2.1.5) ;

якщо на інтервалі функція непарна, то для всіх мають місце рівності й

(2.1.6) .

Ця обставина підказує вихід з положення, при якому функція задана не на інтервалі , а тільки на інтервалі : функцію можна продовжити на весь інтервал парним або непарним образом, а потім зробити розкладання Фур'є, відповідно по косинусах (випадок (2.1.5)) або по синусах (випадок (2.1.6)).