1.1.2. Параметрический t-критерий Стьюдента.

Если измерения проведены по шкале интервалов и установлено, что распределение признака не отличается от нормального, тогда рекомендуется использовать t-критерия Стьюдента, который напрямую определяет значимость различий между средними значениями двух выборок, при этом, не требует, чтобы выборки были одинаковыми по объему и определяется только стандартным отклонением и объемом этих выборок.

Мы приводим формулу по (Сосновский Б.А. (1979г ))

,

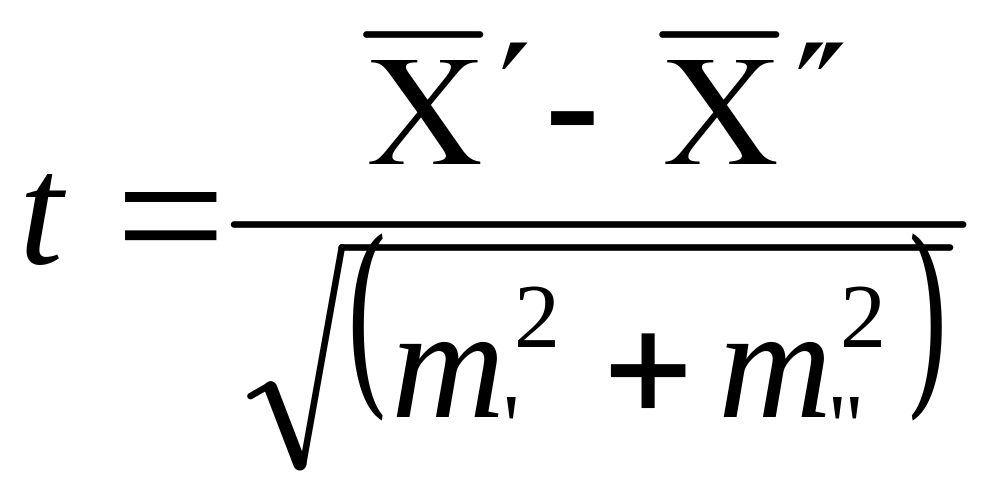где и - средние арифметические, различия, между которыми проверяются;

и - соответствующие ошибки средних, рассчитываемые по формуле: , где  - среднеквадратичное отклонение, N- объем каждой выборки.

При этом считаем нужным рекомендовать за брать большее, а за - меньшее из двух сравниваемых средних значений.

Для определения наличия (отсутствия) значимости различий на уровне исследуемого признака полученное t_набл необходимо сравнить с t_табл. (см. таблицу 2 Приложения). Для нахождения табличного значения необходимо вначале определить число степеней свободы по формуле: f=n₁+n₂-2 где n₁ и n₂ –объем первой и второй выборки. Если выполняется условие, что t_набл > t_табл. _=0,01, то можно говорить о том, что различия между средними по выборкам статистически достоверны. Если t_{табл/ =0,05} < t_набл < t_{табл =0,01}, тогда мы говорим о том, что у нас нет оснований делать однозначные выводы потому, что попали в «зону неопределенности». Если t_набл < t_табл. _=0,05, тогда мы имеем право однозначно утверждать, что значимых различий по данному признаку не существует.

Пример 1.. Перед студентом стояла задача определить, значимы ли различия по уровню ригидности между молодыми и пожилыми людьми. В качестве диагностического инструментария была использована 6-ая шкала ММРI. Выборка составила 12 испытуемых в возрасте 20 – 22 года и 10 испытуемых в возрасте 55 – 60 лет (небольшой объем выборки определяется тем, что наша задача сводится к показу общей схемы расчетов). Проведенные эмпирические исследования дали следующие результаты (приводится в стенах).

Молодые: 48;44;52;40;53;58;41;38;47;40;51;48.

Пожилые: 50;49;64;60;54;48;59;68;55;50.

По правилам статистического анализа необходимо определить характер распределения, но мы пойдем на допущение, что характер распределения не отличается от нормального.

Сформулируем нулевую и альтернативную статистические гипотезы: Н₀: люди пожилого и молодого возраста статистически достоверно не различаются по уровню ригидности; Н₁: люди пожилого и молодого возраста статистически достоверно различаются по уровню ригидности.

Проверим гипотезы.

1. Рассчитаем средние значения по каждой выборке. Для молодых =46,7; для пожилых =55,7.

2. Приступим к расчету m по каждой выборке. Расчет удобнее производить в табличной форме (первая строка – индивидуальные значения, вторая строка- среднее значение для всей выборки, третья строка-разность между индивидуальными значениями и средним, четвертая строка – квадрат разницы).

Таблица 1. (молодые)

48	44	58	40	53	58	41	38	47	40	51	48	
46,7	46,7	46,7	46,7	46,7	46,7	46,7	46,7	46,7	46,7	46,7	46,7
1,3	-2,7	11,3	-6,7	5,3	11,3	-5,7	-8,7	0,3	-6,7	4,3	1,3
1,7	7,3	127,7	44,9	28,1	127,7	32,5	75,7	0,1	44,9	13,5	1,7	505,8

Рассчитаем среднеквадратичное отклонение ( ):

Рассчитаем ошибку средней:

Таблица 2 (пожилые)

50	49	64	60	54	48	59	68	55	50	
55,7	55,7	55,7	55,7	55,7	55,7	55,7	55,7	55,7	55,7
-5,7	-6,7	8,3	4,3	-1,7	-7,7	3,3	12,3	-0,7	-5,7
32,5	44,9	68,9	18,9	2,9	59,9	10,9	151,3	0,5	32,5	422,2

Рассчитаем среднеквадратичное отклонение:

Рассчитаем ошибку средней:

Следующий этап – подставить полученные значения в основную формулу:

Полученное значение t эмпирическое или наблюдаемое необходимо сравнить со значением t табличным. Для нахождения t табличного рассчитаем число «степеней свободы» f по формуле f=n₁ + n₂ – 2, где n₁ и n₂ объем первой и второй выборки. В нашем случае f= 12 +10 –2 = 20. По таблице 2 приложения для данного числа «степеней свободы» находим t _табл. для _{= 0,05} и _{= 0,01}. t _табл.=2,845 при _{= 0,01} и t _табл.=2,086 при _{= 0,05}. По правилу принятия решений, если t _набл. превосходит t _табл. при = 0,01, тогда мы отвергаем Н₀ и принимаем Н₁ и можно говорить о статистически достоверной значимости различий на уровне средних значений двух выборок. В нашем случае 4,44 > 2,845, поэтому мы говорим о том, что статистически достоверно в 99 случаях из 100 ригидность пожилых людей будет выше, чем у молодых.