14. Спектральные плотности мощности: физический смысл и свойства.????

Возможно представление случайных процессов не только во временной, но и в частотной области. Для этого Н. Винер и П. Хинчин применили интеграл Фурье к корреляционным функциям [25]:

.

(1.67)

Полученная функция S_uu() называется спектральной плотностью мощности и определяет распределение мощности случайного процесса по частоте. Эта функция четна и ограничена по частоте (S()=0). Интеграл от спектральной плотности равен мощности сигнала в заданном частотном диапазоне:

;	(1.68)
.	(1.69)

Выражение (1.69) определяет полную мощность сигнала.

Поскольку и k(), и S() четны, часто при изображении графиков ограничиваются правой полуплоскостью. На рис.1.11. показаны графики S(), соответствующие корреляционным функциям рис.1.10,a и b.

Из выражений (1.68) и (1.69) можно определить практическую ширину спектра случайного сигнала:

:

(1.70)

где m - доверительный коэффициент.

Практически это сводится к вычислению неопределенного интеграла в левой части (1.70) с последующим решением полученного уравнения относительно _b .

15. Полная и условная энтропия.

Полная энтропия, которая может рассматриваться как совместная неопределённость ансамбля из двух независимых источников:

.

(1.91)

Здесь N и М - количество различных состояний x_i и y_i .

Предположим вначале, что источники независимы. Тогда на основе формулы произведения вероятностей можно записать:

p(x_i,y_j)= p(x_i)p(x_j),

Поскольку 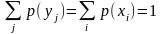(вероятность полной группы событий), окончательно имеем:

H(X,Y)=H(X)+H(Y),

(1.92)

то есть, энтропия ансамбля из двух независимых источников равна сумме их энтропий.

Предположим теперь, что источники зависимы. Тогда, согласно формуле Байеса

P(xi,yj)=p(xi) p(yj|xi)= p(yj) p(xi|yj) (1.94)

(1.93)

В выражении (полная группа событий); тогда первый член представляет энтропию H(x). Во втром члене сумма называется частной условной энтропией (неопределённостью состояния y_j относительно совершившегося состояния x_i), а вся сумма представляет собой математическое ожидание частных условных энтропией и называется условной энтропией:

.

условной энтропии. 

    Найдем энтропию сложного опыта       в том случае, если опыты не являются независимыми, т.е. если на исход  оказывает влияние результат опыта  . Например, если в ящике всего два разноцветных шара и   состоит в извлечении первого, а   – второго из них, то   полностью снимает неопределенность сложного опыта       , т.е. оказывается H(      )  = H( ), а не сумме энтропии, как следует из (1.5).

    Связь между   на     могут оказывать влияние на исходы из  , т.е. некоторые пары событий Ai  Bj не являются независимыми. Но тогда в (1.6)   p (Ai  Bj) следует заменять не произведением вероятностей, а, согласно:

– вероятность наступления исхода Bj при условии, что в первом опыте имел место исход Ai. Тогда:

    При подстановке в (1.6) получаем:

    В первом слагаемом индекс j имеется только у B; изменив порядок суммирования, получим члены вида:

    Однако,

поскольку

образует достоверное событие (какой-либо из исходов опыта  при условии, что в опыте   реализовался исход Ai – будем называть ее условной энтропией. Если ввести данное понятие и использовать его обозначение, то второе слагаемое будет иметь вид:

 (1.9)

где    есть средняя условная энтропия опыта   при условии выполнении опыта  . Окончательно получаем для энтропии сложного опыта:

 (1.10)

    Полученное выражение представляет собой общее правило нахождения энтропии сложного опыта. Совершенно очевидно, что выражение (1.5) является частным случаем (1.10) при условии независимости опытов   и  .

    Относительно условной энтропии можно высказать следующие утверждения:

1. Условная энтропия является величиной неотрицательной.   = 0 только в том случае, если любой исход  полностью определяет исход   (как в примере с двумя шарами), т.е.

    В этом случае H (        ) = H  (   ).

2. Если опыты   и   независимы, то  , причем это оказывается наибольшим значением условной энтропии. Другими словами, опыт   не может повысить неопределенность опыта  ; он может либо не оказать никакого влияния (если опыты независимы), либо понизить энтропию  .

    Приведенные утверждения можно объединить одним неравенством:

 (1.11) т.е. условная энтропия не превосходит безусловную.

3. Из соотношений (1.10) и (1.11) следует, что

 (1.12)

причем равенство реализуется только в том случае, если опыты   и   независимы.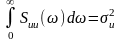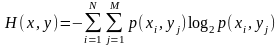