5. Дискретное преобразование Фурье.???

Одномерное преобразование Фурье определяется интегралом вида:

(1)

Двумерное преобразование Фурье определяется следующим интегралом:

(2)

Но, на практике, Фурье-преобразование необходимо выполнять численно, что можно сделать, например, вычисляя определенные интегралы в формулах для всевозможных значений частот каким-либо методом численного интегрирования. Пусть исходная функция определена на интервале . Следовательно, на этом же интервале будет производиться интегрирование в выражении (1). Будем вычислять значение Фурье-образа в равноотстоящих по частоте с шагом точках и воспользуемся для этого методом прямоугольников с шагом , причем:

; ; . (3)

В результате из формулы непрерывного Фурье-преобразования (1) приходим к выражению:

(4)

которое называется дискретным преобразованием Фурье (ДПФ). На основе формулы (4) построен наиболее удобный и быстрый способ численного Фурье-преобразования. Вообще говоря, ДПФ может рассматриваться, как это часто делается, безотносительно к непрерывному Фурье-преобразованию, а именно как преобразование одного массива чисел в другой , и обычно записывается в виде:

, . (5)

Множитель выбирается из соображений симметрии и не является принципиальным.

В ДПФ как исходная функция, так и результат преобразования, представляют собой выборки некоторых функций. Пользуясь свойствами Фурье-преобразования, можно заметить, что ДПФ есть выборка длиной чисел с шагом Фурье-образа выборки с шагом исходной функции на интервале . Как следует из теоремы Котельникова, ДПФ точно соответствует непрерывному Фурье-преобразованию, если преобразуемая функция есть функция с финитным спектром, т.е. если ее Фурье-образ отличен от нуля только в области , и если шаг выборки исходной функции удовлетворяет условию , т.е. .

/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////// Дискретное преобразования Фурье. Как следует из формулы (19.7) Х_T(jω) имеет периодическую структуру с ω_д = 2π/Т. При­чем, как и спектр аналогового сигнала X(jω) спектр дискретного сигнала Х_T(jω) является сплошным (см. рис. 19.6, 6). Вместе с тем при цифровой обработке сигналов используется не только дис­кретизация во времени, но и дискретизация в частотной области.

Для сигнала x(t) ограниченного во времени интервалом Т_с (рис. 19.12, а) справедлива обратная теорема Котельникова, которая может быть получена из (19.3) путем замены 

С учетом вышеизложенного дискретное преобразование Фурье (ДПФ) можно получить, если в преобразовании (19.8) сделать за­мену ω= nΔω. Тогда получим

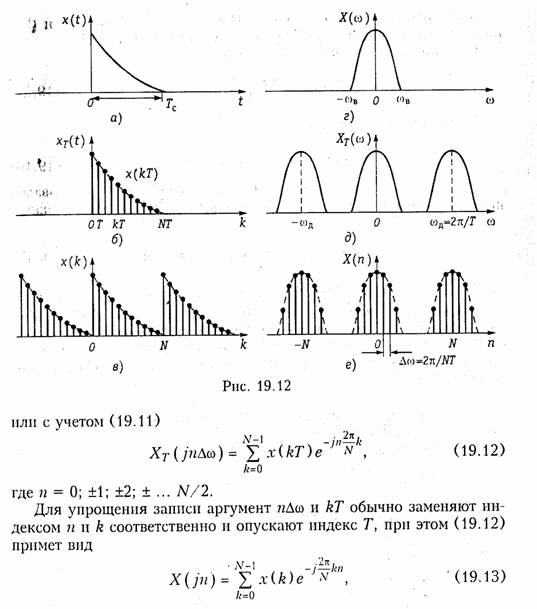
которое определяет прямое ДПФ.

С помощью (19.13) можно определить отсчеты спектра X(jn) по временным отсчетам сигнала x(k).

Обратное ДПФ можно получить из (19.13) воспользовавшись дуальностью прямого и обратного преобразований Фурье:

При  k  < О  обратное преобразование  Фурье определит x(k), расположенную слева от 0 (рис. 19.12, в).

Для ДПФ по аналогии с непрерывными преобразованиями Фу­рье справедливы основные теоремы и свойства (см. § 9.2).

В частности, свойство линейности

т.  е.  сдвиг последовательности отсчетов сигнала на т интервалов приводит лишь к изменению фазового спектра дискретного сигнала.