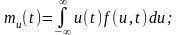3. Случайные процессы: классификация и примеры. Ансамбль реализаций.

. Случайный процесс - это обобщение случайной величины при рассмотрении ее с введением дополнительной координаты времени.

Классическим методом описания случайного процесса является ансамбль реализаций - совокупность случайных функций, наблюдаемых одновременно на выходах множества однотипных объектов. В каждый момент времени t₀ можно получить совокупность значений для каждой случайной функции (это называется сечением процесса в момент t₀), которая является случайной величиной.

Определим основные понятия теории вероятностей из раздела случайные величины. Существует два способа описания случайных величин: с помощью плотности распределения вероятностей f(u) и функции распределения F(x). Перечислим их свойства.

Для плотности распределения:

f(u)0|u
	(ограниченность);
	(нормировка);
	(интервальная вероятность).

Аналогично для функции распределения

F(-)=0; F()=1	(граничные значения);
F(b)F(a) при b>a	(монотонность);
(aP<b)=F(b)-F(a) Случайные процессы во времени описываются в основном тремя функциями: математическим ожиданием, дисперсией и корреляционной функцией: (1.64) (1.65) (1.66) Здесь f2(u1,u2;t1,t2)-двумерная плотность распределения вероятности.	(интервальная вероятность).

4. Математическое описание случайных процессов. Плотности распределения вероятностей.

Случайный процесс - это обобщение случайной величины при рассмотрении ее с введением дополнительной координаты времени.

Классическим методом описания случайного процесса является ансамбль реализаций - совокупность случайных функций, наблюдаемых одновременно на выходах множества однотипных объектов. В каждый момент времени t₀ можно получить совокупность значений для каждой случайной функции (это называется сечением процесса в момент t₀), которая является случайной величиной.

Непрерывную случайную величину можно также задать, используя другую функцию, которую называют плотностью распределения или плотностью вероятности (иногда ее называют дифференциальной функцией).

Плотностью распределения вероятностей непрерывной случайной величины Х называется функция f(x) – первая производная от функции распределения F(x). Плотность распределения также называют дифференциальной функцией. Для описания дискретной случайной величины плотность распределения неприемлема. Смысл плотности распределения состоит в том, что она показывает как часто появляется случайная величина Х в некоторой окрестности точки х при повторении опытов. После введения функций распределения и плотности распределения можно дать следующее определение непрерывной случайной величины. Из формулы P{Α ≤ X < Β}=F(Β)-F(Α)следует, что вероятность попадания случайной величины в заданный интервал определяется скоростью изменения функции распределения вероятностей на этом интервале. Скорость изменения непрерывной функции равна ее производной. Это позволяет ввести новую функцию для задания случайной величины. Рассмотрим снова вероятность попадания случайной величины в интервал [x,x+Δx]: P{x≤X<x+Δx}=F(x+Δx)-F(x).

Пусть Х - непрерывная случайная величина. Тогда для малых значений Δx эта вероятность будет также достаточно малой. Поделим ее на Δx и перейдем к пределу при Δx →0:

limΔx →0(P{x≤X<x+Δx}/Δx)=limΔx →0(F(x+Δx)-F(x))/Δx).

Если это предел существует, то он равен производной от функции распределения F(x):

limΔx →0(F(x+Δx)-F(x))/Δx)=F'(x)=f(x).

Функция f(x) называется плотностью распределения вероятностей случайной величины Х. Из определения следует, что при малых значениях Δx справедливо равенство:

P{x≤X<x+Δx}≈f(x)*Δx

Рассмотрим свойства плотности распределения f(x).

1. Всегда f(x)≥0, так как функция F(x) является неубывающей функцией.

2 Для функции распределения F(x) справедливо равенство:

F(x)=-∞∫xf(t)dt.

Действительно, так как по определению f(x)=F'(x), то F(x) является первообразной функцией по отношению к плотности распределения f(x). Следовательно,

-∞∫∞f(t)dt=F(t)-∞ιx=F(x)-F(-∞)=F(x)-0=F(x.)

3. Вероятность попадания случайной величины в заданный интервал [Α ; Β] равна:

P{Α≤X<Β}=Α∫βf(t)dt.

Действительно, в соответствии с формулой Ньютона-Лейбница этот определенный интеграл равен F(Β)-F(Α). По 3-му свойству функции распределения вероятностей эта разность и представляет собой вероятность P{Α≤X<Β} .

4. Интеграл от плотности распределения вероятности по всей области задания случайной величины равен единице:

-∞∫∞f(t)dt=1 .

Рвенство -∞∫∞f(t)dt=1 представляет условие нормировки вероятностей для непрерывных случайных величин. По смыслу данный интеграл есть не что иное, как F(∞)=1. Условие нормировки вероятностей часто используется для определения неизвестного параметра закона распределения.

Для иллюстрации геометрического смысла перечисленных свойств приведем пример графика плотности распределения вероятностей. Для большей наглядности на рис. представлен также график соответствующей функции распределения вероятностей.