Теорема Ролля.
Если функция y=f(x) определена и непрерывна в замкнутом промежутке [a,b] имеет в каждой точке открытого промежутка (a,b) конечную производную и на концах промежутка принимает равные значения f(a)=f(b), тогда найдется хотя бы одна такая точка x0, принадлежащая (a,b), в которой производная равна нулю, т.е. f ‘ (x0) = 0.
Доказательство:
Обозначим:
М = sup {f(x)}, x принадлежит [a,b] ,
m = inf {f(x)}, x принадлежит [a,b],
m <= M,
причем, если f(x)=const, то m=M, а если f(x) не равно const, то m<M.
Рассмотрим различные случаи:
f(x)=const
f’(x)=0 в любой точке x, принадлежащей (a,b).
f(a) = f(b) = sup {f(x)}, x принадлежит [a,b], => внутри промежутка [a,b] существует точка минимума х=х0. По теореме Ферма в точке минимума производная равна нулю => f’(x0)=0.
f(a) = f(b) = inf {f(x)}, x принадлежит [a,b], => внутри промежутка [a,b] существует точка максимума х=х0. По теореме Ферма в точке максимума производная равна нулю => f’(x0)=0.
f(a)=f(b) не равно m, x=x1,
f(a)=f(b) не равно М, x=x2,
f’(x1)=0, f’(x2)=0.
Внутри промежутка существует и точка минимума, и точка максимума.
Теорема Лarранжа. Условие возрастания и убывания функций.
Если функция y=f(0) определена и непрерывная в замкнутом пространстве [a,b] и в каждой точке открытого промежутка (а,в) имеет конечную производную, то найдется такая точка х=с, в кот.выполняется равенство:
(1)
Доказательство:
введем вспомогательную функцию F(x)
= f(x)+
x,
где
-некоторая
постоянная. Функция F(x)
удовлеторяет двум первым условиям
т.Ролля. Потребуем чтобы удовлетворялось
и третье условие т.Ролля.
F(a)=F(b)
=> f(a) +
a=f(b)+
b=>
=
Согласно
т.Ролля сущ. X=с
(a,b),
в которой Fштрих(С)=0
Fштрих(х)=
(x)
+
=>
Fштрих(С)
=
(с)
+
=0
=>
=
-
(с)
Приравнивая 2 значения , получаем формулу (1)
Следствие 1:
Функция y=f(x) возрастает в тех промежутках, где производная положительна, и убывает там, где производная отрицательна.
Следствие 2:
Если (x)=0 в каждой точке некоторого промежутка, то в этом промежутке f(x) = const
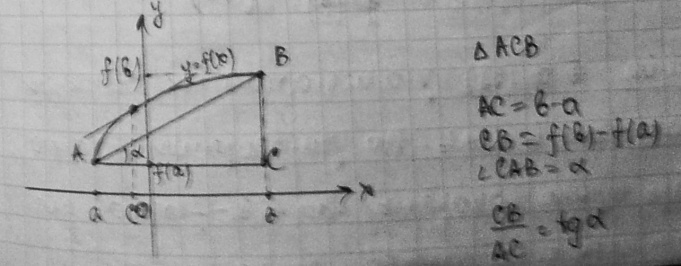
Рассмотрим геометрическй смысл т.Лагранжа (формула1)
Teoрeмa Коши, правило Лопиталя.
Теорема Коши
Следствием т.Коши является правило Лопиталя, позволяющее с помощью производных раскрывать неопределенности: [0/0], [бесконечноть/бесконечность]
Правило Лопиталя
Пусть
функции f(x)
и g(x)
удовлетворяют всем условиям т.Коши,
причем
=0,
=0
или же это равно бесконечности, тогда
существует:
(такая запись точной формулировки)
Доказательство:
Обозначим
в=х, с=
(кси), х
а,
но т.к. a<
<x,
то по т. О переменной
из них следует, что f(a)=0, g(a)=0
=
Начиная с некоторого момента х и кси при стремлении к а пробегают одни и те же значения => переменную кси можно заменить на переменную х => получаем формулу (из тогда существует).
Аналогично доказывается случай с бесконечностями.
Примеры:
