2.7. Закономерности случайных процессов изменения технического состояния автомобилей (закономерности второго вида)

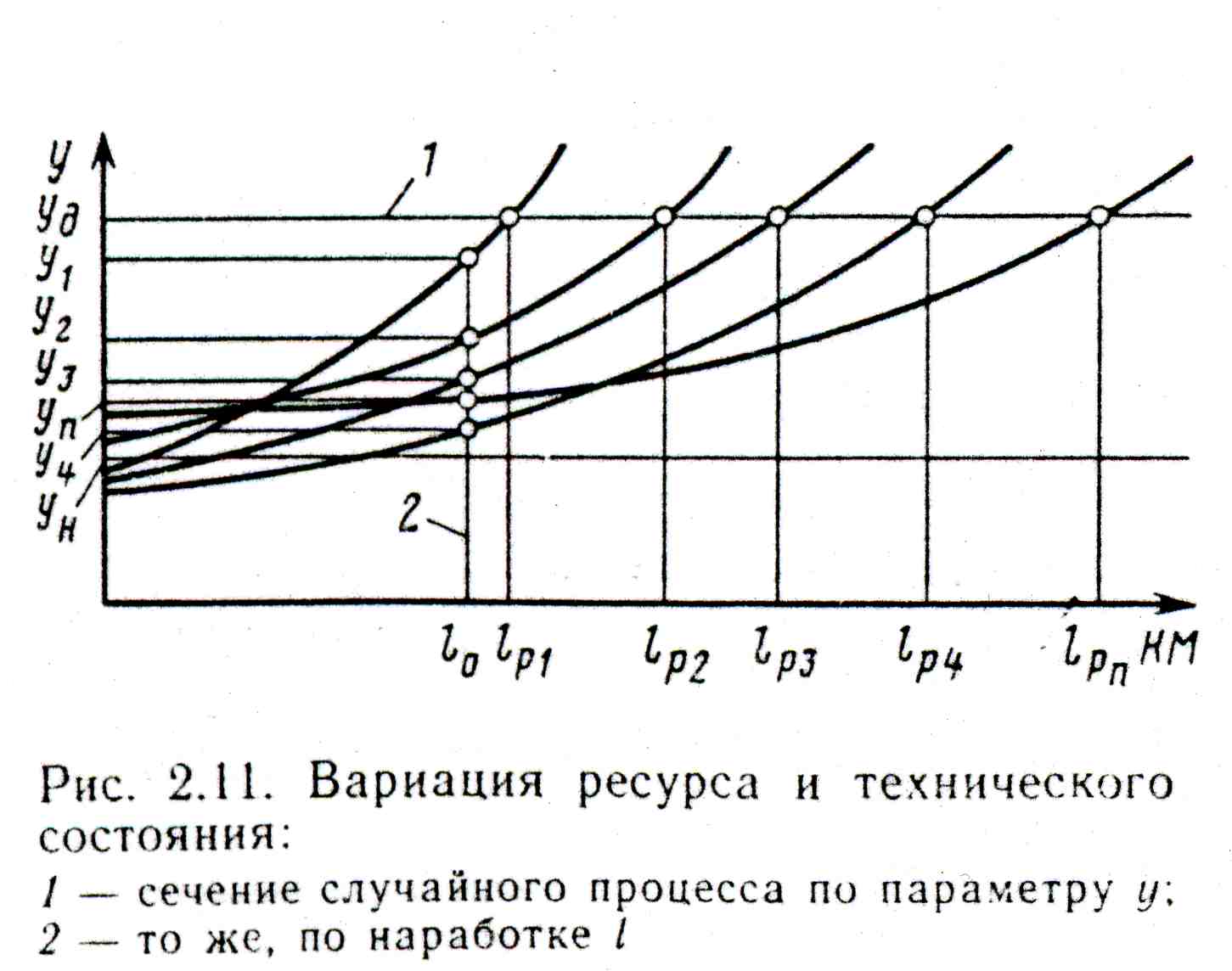
Как уже отмечалось, под влиянием условий эксплуатации, квалификации персонала, неоднородности самих изделий и их начального состояния и других факторов интенсивность и характер изменения параметра технического состояния у разных автомобилей будут различными. Поэтому если зафиксировать значение параметра, например, на уровне у_д (рис. 2.11), то моменты достижения этого состояния (ресурса) l_р. у разных изделий будут различны, т. е. наработка на отказ будет случайной величиной и будет иметь вариацию. В связи с этим возникает вопрос, как установить момент контроля и обслуживания изделий? Если зафиксировать определенную наработку к моменту контроля и обслуживания автомобиля Lо, то неминуемы вариация показателя его технического состояния и, как следствие, вариация трудоемкости и продолжительности выполнения' работ по восстановлению технического состояния. Поэтому важно знать, какую трудоемкость и продолжительность учитывать и нормировать при организации технического обслуживания и ремонта.

Совершенно очевидно, что решение этого вопроса во многом зависит от вариаций случайной величины. Характеристиками случайной величины X при n реализациях служат :

Среднее значение

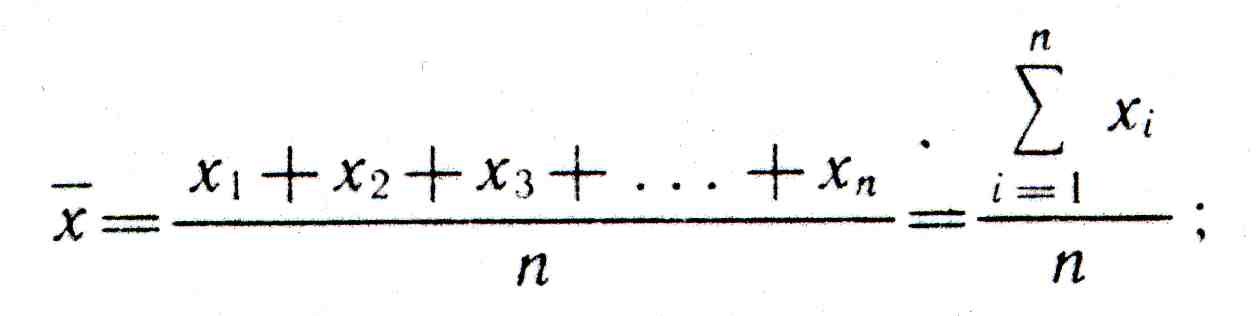
среднеквадратическое отклонение

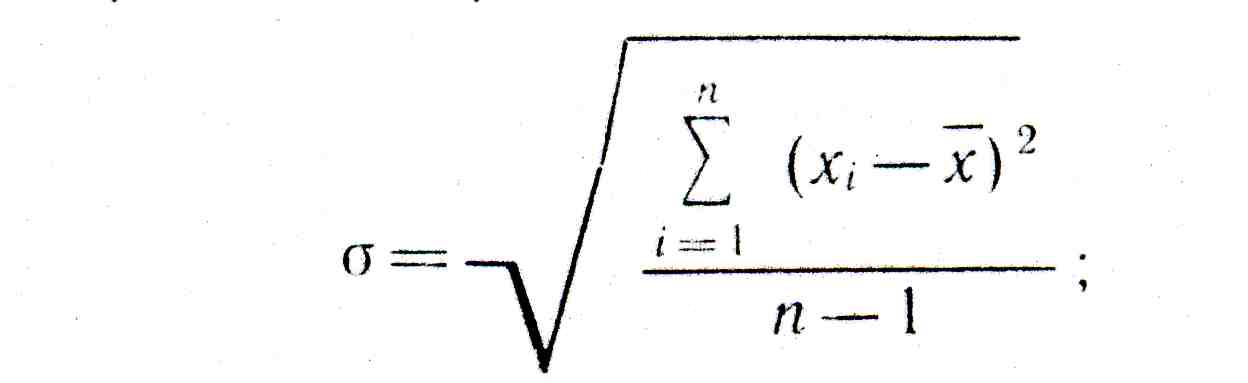
дисперсия D= σ²; коэффициент вариации V_x=σ √X.

В технической эксплуатации автомобилей различают случайные величины с малой (V≤0.1), средней (0,1<V≤0,33) и большой вариацией (V>0,33). Фактически полученный в результате обработки экспериментальных данных, а также из литературных источников коэффициент v служит для предварительного определения закона распределения данной случайной величины (см. ниже).

Помимо приведенных, важнейшей характеристикой случайной величины служит вероятность — численная мера степени объективно существующей возможности появления изучаемого события. Обычно вероятность обозначается буквой Р. Статистически вероятность события А представляет собой отношение числа случаев, благоприятствующих этому событию, к общему числу случаев п. Вероятность может принимать значения в интервале 0≤P≤1. События, для которых Р=1, называются достоверными, а события, для которых Р≤О, 05, — маловероятными.

Вероятность безотказной работы R (х) * определяется отношением числа случаев безотказной работы изделия за наработку Х: к общему числу случаев, т. е.

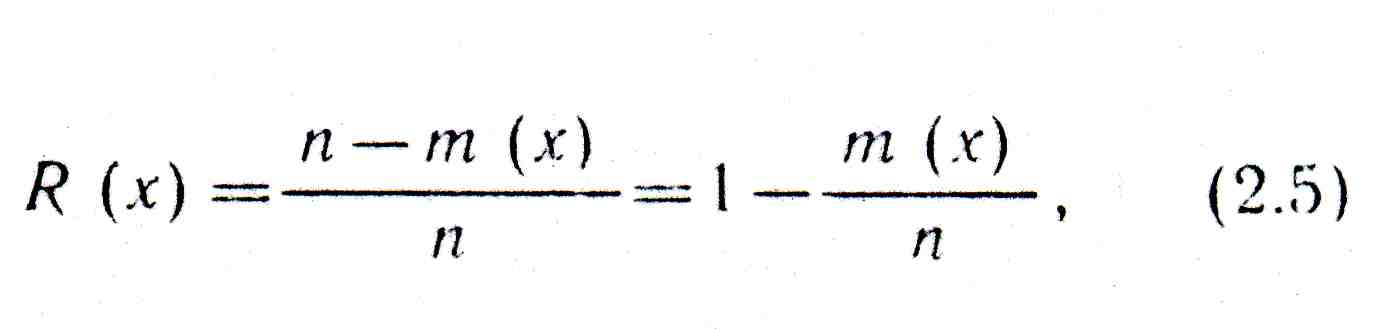
Где m( x) — число отказавших изделий к моменту наработки х.

Вероятность отказа F(x) * является событием, противоположным вероятности безотказной работы, поэтому

F(x)=1-R(x)=m(x)/n. (2.6)

Графическое изображение вероятностей безотказной работы и отказа представлено на рис. 2.12. Эти графики справедливы для невосстанавливаемых изделий, т. е. подлежащих замене после первого отказа, и для восстанавливаемых изделий, но для отдельных циклов работы: до первого отказа, между первым и вторым отказом и т. д. Имея значения F (х) или R(х), можно решать следующие практические задачи.

Если X_Y — это заданная наработка агрегата или детали, а X_I — наработка до отказа, то вероятность события Р(x_i>X_Y)=R(x)=γ означает, что с вероятностно Р=γ изделие проработает без отказа больше заданной наработки Xγ. Эта наработка называется гамма-процентной наработкой (ресурсом) до отказа. Обычно γ принимается равной 0,8; 0,85; 0,9; 0,95. Выражение Р(Xi≤Xγ) = F(х) означает, что с вероятностью F(х) изделие откажет при наработке, меньшей или равной Xγ.

Если случайной величиной является продолжительность выполнения какой-либо операции ТО или ремонта, то выражение Р(Xi≤Xγ) = F(х) = 1 -γ означает, что в (1 —γ) случаях потребуется время, меньшое чем Хγ .

Следующей характеристикой случайной величины является плотность ее вероятности (например, вероятности отказа) f(x) — функция, характеризующая вероятность отказа за малую единицу времени при работе узла, агрегата, детали без замены. Если вероятность отказа за наработку Х равна F(X)=M(X)/n то, дифференцируя при п=const получим плотность вероятности отказа

где dm/dx - элементарная “скорость”, с которой в любой момент времени происходит приращение числа отказов при работе детали, агрегата без замены.

Так как f(X)=F’(X), то

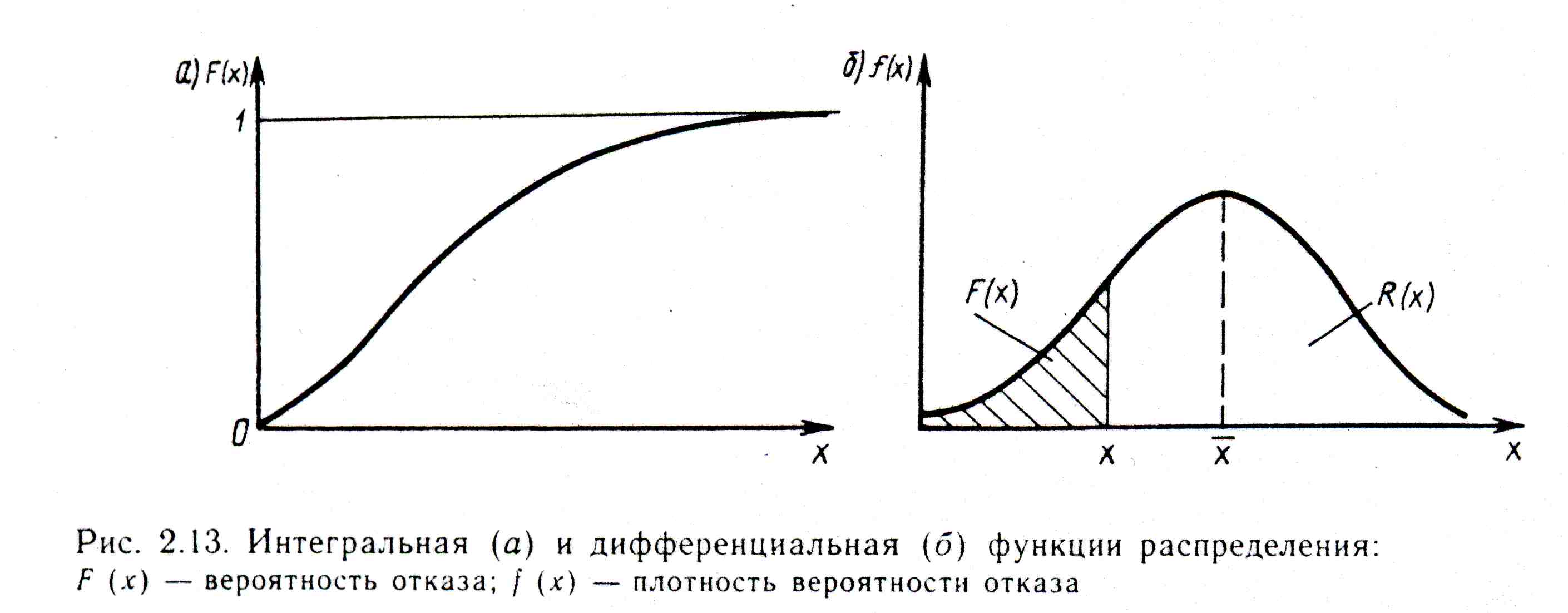
Поэтому F(х) называют интегральной функцией распределения, а f(x) — дифференциальной функцией распределения (рис. 2.13).

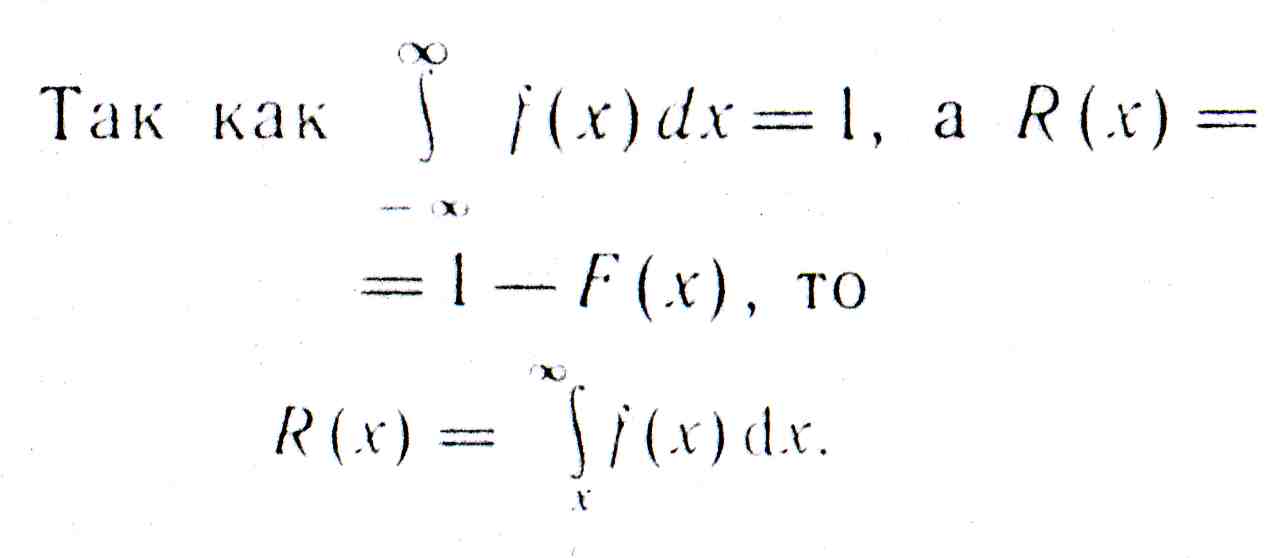
Имя значения F(х) или f(x), можно произвести оценку надежности и определить среднюю наработку до отказа:

На практике, зная f(x), оценивают возможное число отказов m(x), которое может возникнуть за сравнительно небольшой интервал наработки Δx=x₁-x₂. Для этого значение f(x) умножают на число изделий n и величину интервала Δx. Например, при n = 75 f(x)=0,02 тыс. км-1 и Δx = 2 тыс. км получаем f(x)n(x₁-х₂)≈0,02 * 75*2≈3 отказа, т. е. при эксплуатации 75 невосстанавливаемых изделий (или восстанавливаемых изделий - до первого отказа) есть основания ожидать в интервале наработки x₁-x₂ появления 3 отказов и подготовиться соответствующим образом к их устранению. Умножая значение плотности вероятности отказа f(X) на величину интервала наработки, можно получить оценку вероятности отказа изделий в данном интервале. Для того же примера эта вероятность Р(x₁<X<x₂)≈f(x₁)*Δx=0,02*2 = 0,04. Графически эта величина определяется площадью под кривой дифференциальной функции распределения с основанием Δx= x₁- x₂ (см. рис. 2.13,6).

В общем случае f(х), R(х), F(х) получают при сечении случайного процесса в моменты t₁ и t₂ т. д. (рис. 2.9, а). Дифференциальная функция распределения f(х) называется также законом распределения случайной величины. Знание законов распределения случайных величин позволяет более точно планировать моменты проведения и трудоемкость работ ТО и ремонта, определять необходимое количество запасных частей и решать другие технологические и организационные вопросы.

Для процесса технической эксплуатации наиболее характерны следующие законы распределения.

Нормальный закон распределения. Такой закон формируется тогда, когда на протекание исследуемого процесса и его результат влияет сравнительно большое число независимых (или слабозависимых) элементарных факторов (слагаемых), каждое из которых в отдельности оказывает лишь незначительное действие по сравнению с суммарным влиянием всех остальных. Например, наработка до проведения ТО складывается из нескольких (десяти и более) сменных пробегов, отличающихся один от другого. Однако они сопоставимы, т. е. влияние одного сменного пробега на суммарную наработку незначительно, поэтому периодичность ТО подчиняется двухпараметрическому ( ,σ) нормальному закону, для которого имеем:

Для нормального закона при расчетах часто пользуются понятием нормированной функции Ф(г), для которой принимается новая случайная величина z=(x- )/σ, так называемое нормированное отклонение. Тогда

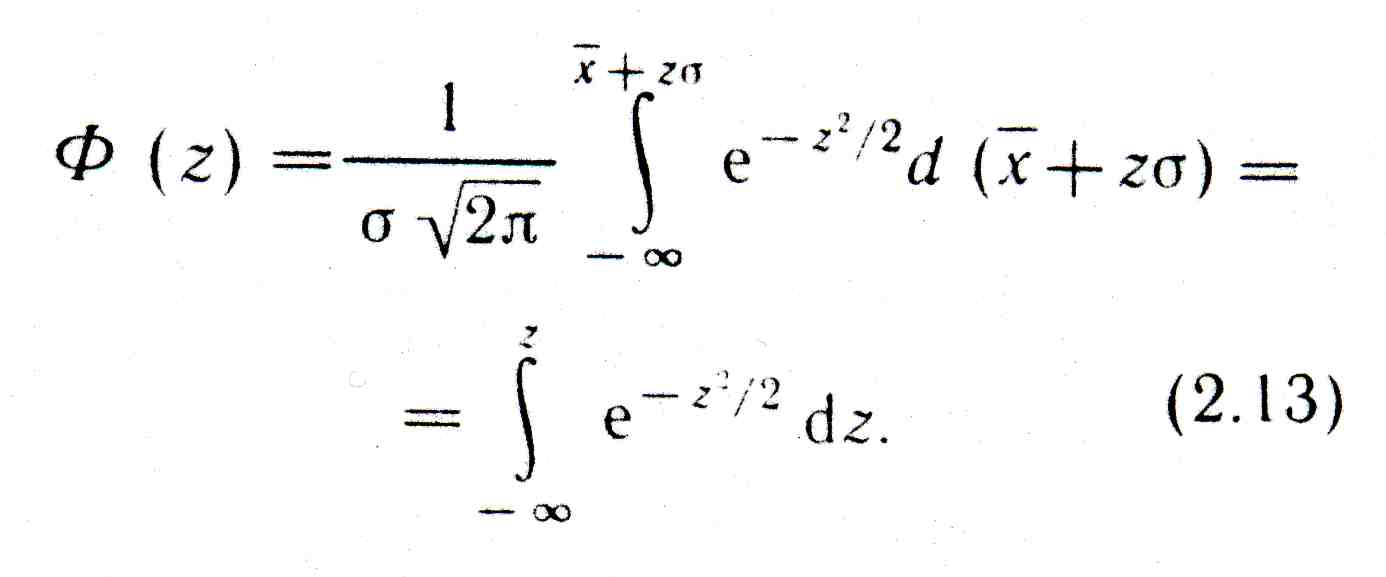
Для нормированной функции составлены таблицы, облегчающие расчеты (табл. 2.9).

Пример. Определить вероятность первой замены детали при работе автомобиля с начала эксплуатации до наработки 70 тыс. км. Распределение наработки до первого отказа подчиняется нормальному закону с параметрами: =95 тыс. км; σ= 30 тыс.км.

Используя понятие нормированной функции, определим нормированное отклонение

z=(x- )/σ=(70-95)/30= -0.83. P(x)=Ф(z)=Ф(-0,83). Из табл. 2.8 находим Ф(-0,83) ≈0,20.

Таким образом, примерно 20 % автомобилей потребует замены деталей при пробеге с начала эксплуатации до 70 тыс. км.

Вероятность отказа в интервале пробега x₁-x₂ определяется разностью P(x₂)-P(x₁)=Ф (z₂)-Ф (z₁).

Для нормального закона V≤0.33

Закон распределения Вейбулла — Гнеденко. Данный закон проявляется в модели так называемого «слабого звена». Если система состоит из группы независимых элементов, отказ каждого из которых приводит к отказу всей системы, то в такой модели рассматривается распределение времени (или пробега) достижения предельного состояния системы как распределение соответствующих минимальных значений x_i отдельных элементов x_c=min(x₁ , x₂ , …x_n). Функция распределения этой величины может быть выражена следующей зависимостью:

где а и b — параметры распределения.

Примером использования распределения Вейбулла-Гнеденко является распределение ресурса подшипника качения, который ограничивается одним из элементов: шарик или ролик, конкретный участок сепаратора и т. д. По аналогичной схеме наступает предельное состояние тепловых зазоров клапанного механизма. Некоторые изделия при анализе модели отказа могут быть рассмотрены как состоящие из нескольких элементов (участков). Это прокладки, уплотнения, шланги, трубопроводы, приводные ремни и т. д. Разрушение указанных изделий происходит в разных местах и при разной наработке, однако, ресурс изделия в целом определяется наиболее слабым его участком. Для этого закона в практических задачах ТЭА коэффициент вариации V=0,4…0,6. Расчет параметров приведен в прил. 2.

Логарифмически нормальный закон распределения. Если на протекание исследуемого процесса и его результат влияет сравнительно большое число случайных и взаимонезависимых факторов, интенсивность действия которых зависит от достигнутого случайной величиной состояния, то возникают условия для логарифмически нормального закона. Эта так называемая модель пропорционального эффекта рассматривает некоторую случайную величину, имеющую начальное состояние Xo и конечное предельное состояние Xn . Изменение случайной величины происходит таким образом, что

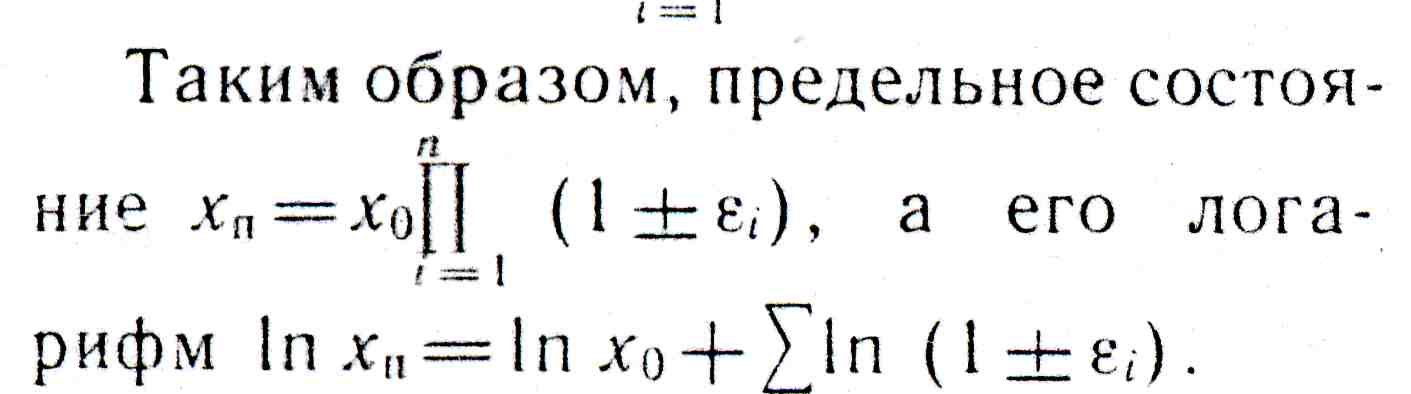
Согласно центральной предельной теореме ln Xn, имеем асимптотически нормальное распределение, как сумма ряда случайных равновеликих и взаимонезависимых величин, а сама величина Xn распределена по логарифмически нормальному закону (см. прил. 2).

В технической эксплуатации этот закон (при v = 0,3…0, 5) встречается при описании процессов усталостных разрушений, коррозии, наработки до ослабления крепежных соединений и в ряде других случаев.

Экспоненциальный закон распределения. Предположим, что в начальный момент X=0 элементы численностью N₀ были исправны. При работе происходят отказы этих элементов таким образом, что независимо от проработанного времени X число отказов (ΔN) в небольшом интервале времени ΔX пропорционально числу оставшихся исправных элементов N_X, а непосредственно перед отказом элемент находится в исправном состоянии, т. е. ΔN/ ΔX= - λNX , г д е λ— положительная постоянная, а знак минус свидетельствует о сокращении N_X при работе. При ΔX→0 имеем dN/dX=- λNX; dN/NX=-λdx. После интегрирования 1п N_X =-λх-1п С, откуда N_X= Cexp[-λX].

При x = 0 C=N₀, откуда N= N₀exp[-λx]. Но N_X/N₀=R(x), тогда вероятность безотказной работы (см. прил. 3) R(х) =ехр [-λx].

Данное уравнение характеризует вероятность безотказной работы при экспоненциальном законе распределения, а λ— параметр потока отказов (называемый также для экспоненциального распределения интенсивностью отказов), равный обратной величине средней наработки на отказ, т. е. λ=1√х. Плотность распределения для экспоненциального закона описывается уравнением

f(x)=λexp[-λx] (2.16)

При этом законе распределения коэффициент вариации V=1.

Экспоненциальный закон распределения является однопараметрическим, что облегчает расчеты и объясняет широкое его применение на практике. В соответствии с теоремой умножения вероятностей вероятность безотказной работы к моменту X+ ΔX равна вероятности безотказной работы в течение времени x умноженной на вероятность безотказной работы за время ΔX, т. е.

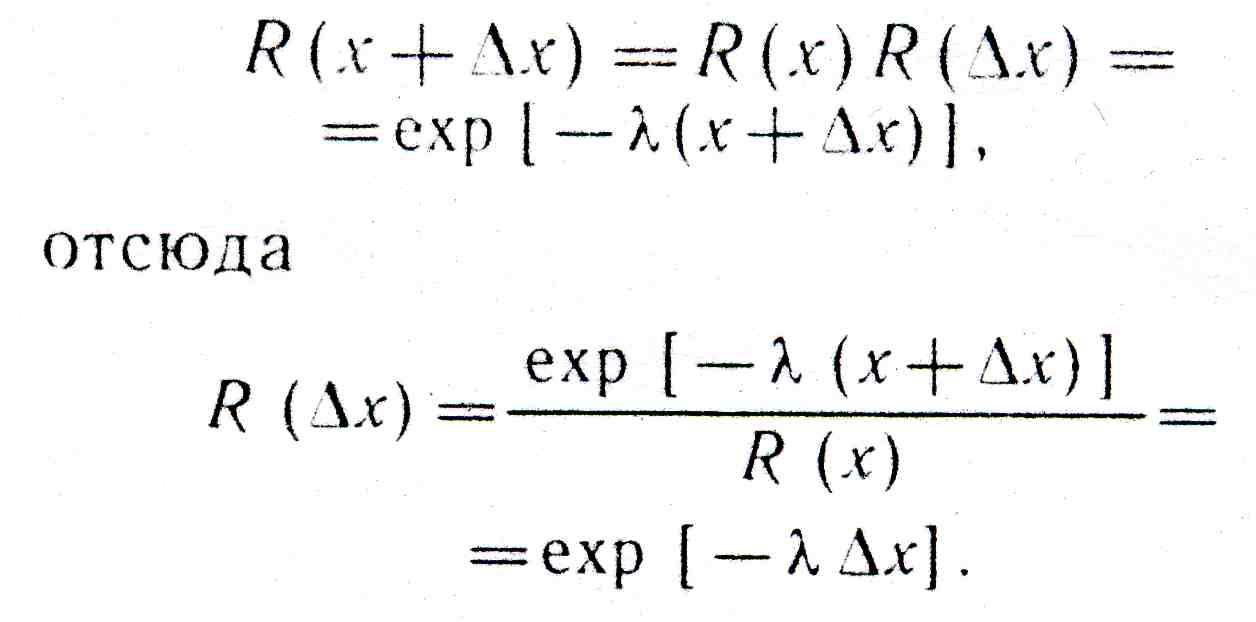
Следовательно, при экспоненциальном законе распределения вероятность безотказной работы не завесит от того, сколько проработало изделие с начала эксплуатации, а определяется конкретной продолжительностью рассматриваемого периода или пробега ΔX называемого временем выполнения задания. Таким образом, рассмотренная модель не учитывает постепенного изменения параметров технического состояния, например, в результате изнашивания, старения и так далее, а рассматривает так называемые нестареющие элементы и их отказы. Экспоненциальный закон используется чаще всего при описании внезапных отказов, продолжительности разнообразных ремонтных, воздействий и в ряде других случаев. Расчет R(х) приведен в прил. 3 .

Важным показателем надежности является интенсивность отказов λ (X) — условная плотность вероятности возникновения отказа невосстанавливаемого изделия, определяемая для данного момента времени при условии, что отказа до этого момента не было. Аналитически для получения(X) необходимо элементарную вероятность dm/(dx) отнести к числу элементов, не отказавших к моменту x, т. е.

Т аким образом, интенсивность отказов равна плотности вероятности отказа, деленной на вероятность безотказной работы для данного момента времени или пробега.

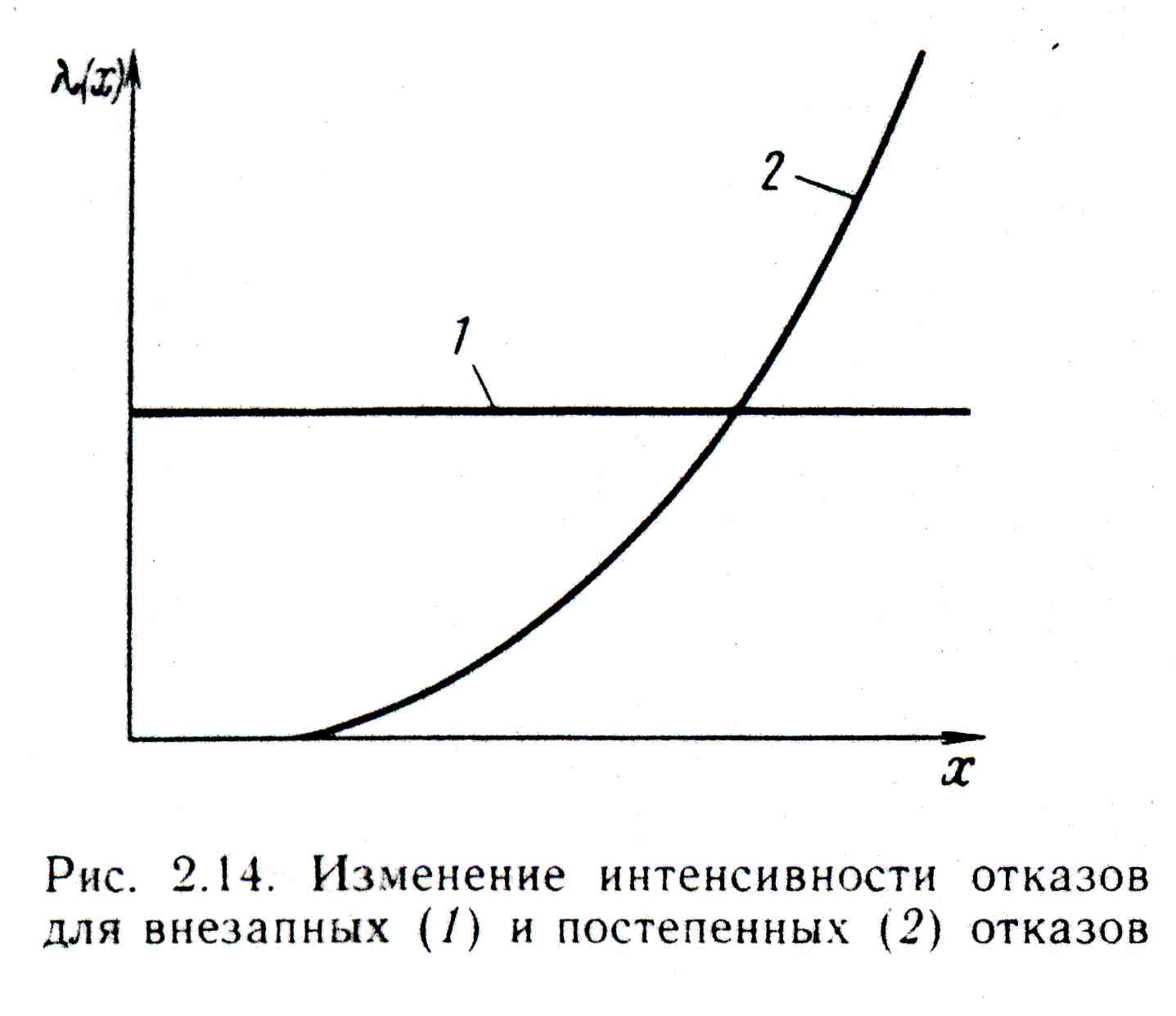
Зная интенсивность отказов, можно для любого момента времени или пробега определить вероятность безотказной работы. На рис. 2.14 приведены λ(Х) для двух характерных случаев: при внезапных и постепенных отказах. Последние описывают безотказность так называемых «стареющих» элементов.

2.8. ЗАКОНОМЕРНОСТИ ПРОЦЕССОВ ВОССТАНОВЛЕНИЯ (ЗАКОНОМЕРНОСТИ ТРЕТЬЕГО ВИДА)

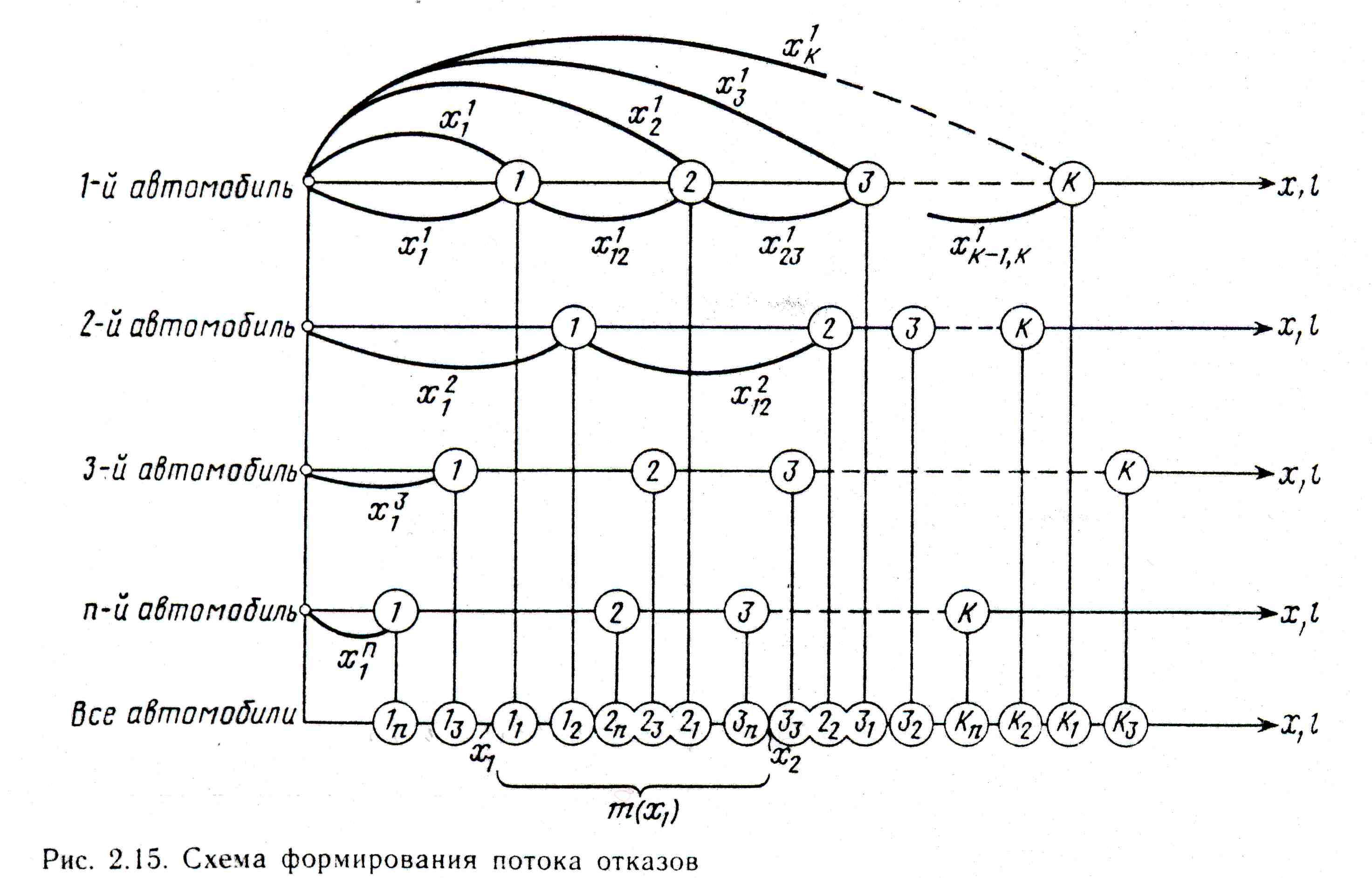
Ранее были рассмотрены два вида закономерностей: изменение параметров технического состояния автомобилей по времени или пробегу и вариации параметров технического состояния. Эти закономерности достаточно точно характеризуют надежность автомобилей и их элементов, т. е. позволяют оценить среднюю наработку на отказ, вероятность отказа автомобиля при определенном пробеге, ресурс его агрегатов и др. Для рациональной организации производства необходимо, кроме то-го, знать, сколько автомобилей с отказами данного вида будет поступать в зону ремонта в течение смены (недели, месяца), будет ли их количество постоянным или переменным и от каких факторов оно зависит, т. е. речь идет не только о надежности конкретного автомобиля, но и группы автомобилей, например, автомобилей данной модели, колонны, АТП. При отсутствии этих сведений нельзя рационально организовать производство, т. е. определить необходимое число рабочих, размеры производственных площадей, расход запасных частей и материалов. Взаимосвязи между показателями надежности автомобилей и суммарным потоком отказов для группы автомобилей изучают с помощью закономерностей третьего вида, которые характеризуют процесс восстановления — возникновения и устранения неисправностей изделий во времени. Предположим, что фиксируются моменты появления одинаковых отказов в группе из n автомобилей (рис. 2.15). Очевидно, что наработки на отказы, во-первых, случайны для каждого автомобиля и описываются соответствующей функцией F(х) или f(х). Во-вторых, эти наработки независимы у разных автомобилей. В-третьих, при устранении отказа в зоне ремонта безразлично, от какого автомобиля поступает отказ и какой он по счету. К важнейшим характеристикам закономерностей третье-го вида относятся средняя наработка до k-го отказа, средняя наработка между отказами для п автомобилей, коэффициент полноты восстановления ресурса, ведущая функция потока отказов Ω(х) и параметр потока отказов W(X) .

Средняя наработка до k-го отказа

Средняя наработка между отказами для n автомобилей получается из (2.19). Между первым и вторым

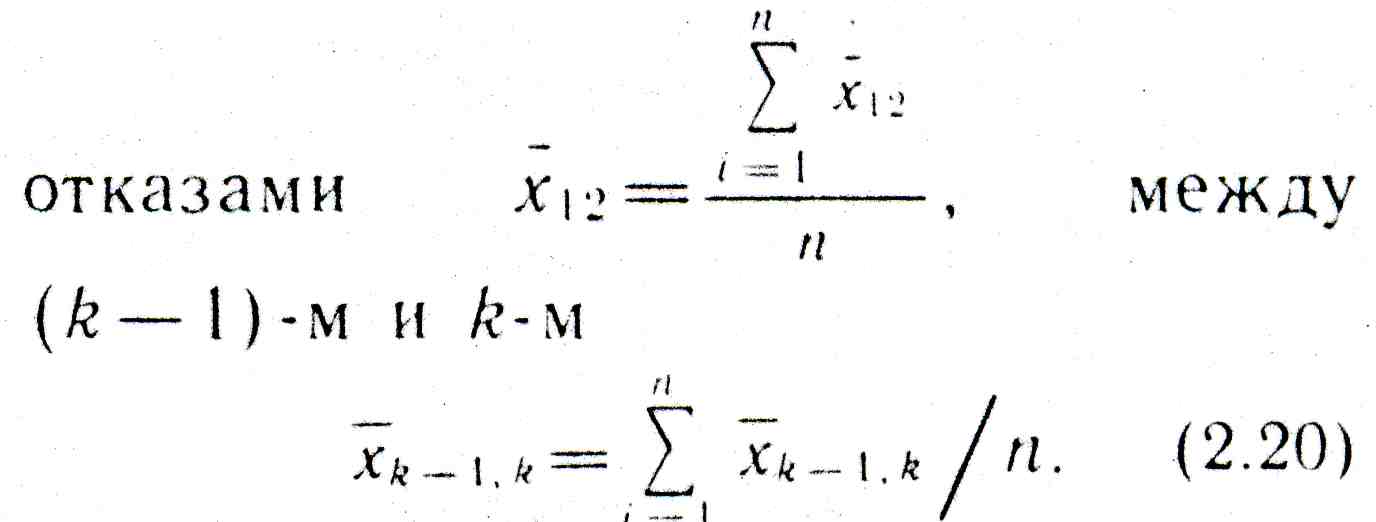
Коэффициент полноты восстановления ресурса характеризует возможность сокращения ресурса после ремонта, т.е. качество произведенного ремонта. После первого ремонта (между первым и вторым отказами) этот коэффициент η1=X1+2√X1, после k-го отказа η=XK,K+1√X1 . При этом 0≤η≤1

Сокращение ресурса после первого и последующих ремонтов, которое необходимо учитывать при планировании и организации работ по обеспечению работоспособности, объясняется: частичной заменой только отказавших деталей при значительном сокращении надежности других, особенно сопряженных, использованием в ряде случаев запасных частей и материалов худшего качества, чем при изготовлении автомобиля; низким технологическим уровнем работ.

Ведущая функция потока отказов (функция восстановления) Ω(х) определяет накопленное количество первых и последующих отказов изделия к наработке х. Как следует из рис. 2.16, из-за вариации наработок на отказы происходит их смещение, а функции вероятностей первых и последующих отказов F1, F2, ..., FK частично накладываются друг на друга. Поэтому, если вероятное количество отказов, например, к пробегу х1 определяется как к Ω (х} = F1(х1}, так как при х<х1 возникают только первые отказы, то для момента х2 общее количество отказов определяется суммированием вероятностей первого F1(x2) и второго F2(x2) отказов. Поэтому Ω(x2)=F1(x2)+F2(x2), а в общем виде:

Параметр потока отказов W(x) — это плотность вероятности возникновения отказа восстанавливаемого изделия, определяемая для данного момента времени или пробега:

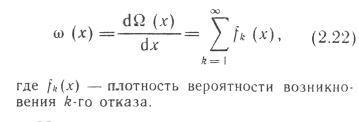
Иными словами, - это отно­сительное число отказов, приходя­щееся на единицу времени или пробе­га одного изделия. Причем при оцен­ке надежности изделия число отказов обычно относят к пробегу, а при оцен­ке потока отказов, поступающих для устранения, — ко времени работы соответствующих производственных подразделений. Следует отметить, что ведущая функция и параметр потока отказов определяются анали­тически лишь для некоторых видов законов распределения. Например, для экспоненциального закона

Пример. Наработка до первой замены накладок сцепления Х₁=58 тыс.км, среднее квадратичное отклонение =10 тыс. км, коэффициент восстановления ресурса =0,6. Определить возможное число замен при пробеге автомобиля 150 тыс км.

Для расчетов используем формулу (2.23), последовательно определяя F₁, F₂, F₃ и т.д.:

(см. табл. 2.9), , , , , вводу того, что мало, последующие расчеты для и других можно не производить. Таким образом, к пробегу 150 тыс. км возможное число замен данной детали составит:

Для практического использования важны некоторые приближенные оценки ведущей функции параметра потока отказов

Из этой формулы следует, что на начальном участке работы, где пре­обладают первые отказы, т. е. F (x)<<1,

Ведущая функция параметра по­тока отказов стареющих элементов для любого момента времени или для пробега удовлетворяет следующему неравенству:

Для рассмотренного выше примера с заменой накладок сцепления, используя формулу (2.26), получим следующую оценку ведущей функции параметра потока отказов при пробеге автомобиля Х =150 тыс. км 3,3 4,3. Таким образом, к пробегу Х в среднем по формуле 2.26 возможно от 3,3 до 4,3 отказов сцепления.

Для любого закона распределения наработка на отказ, имеющая конеч­ную дисперсию U — n'-, ведущая функция параметра потока отказов при достаточно большом значении х определяется по следующей фор­муле:

. (2.27)

При расчете гарантированных за­пасов необходима интервальная оцен­ка ведущей функции параметра потока отказов (для достаточно больших значений х)

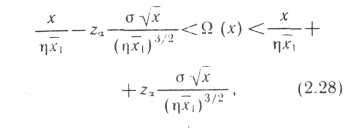
где - нормированное отклонение для нормального закона распределения при условии, что число отказов (замен) с вероятностью будет заключено в данных пределах.

Пример. Определить для условий предыдущего примера (Х₁=58 тыс.км, =10 тыс. км, =0,6) с достоверностью = 0,9 необходимое число накладок сцепления на пробег автомобиля 150 тыс. км. Так как условия задачи требуют обеспечения накладками с вероятностью 90 %, то необходимо определить верхнюю границу потребности в накладках за 150 тыс. км пробега. Определим нормированное отклонение при = 0,9 =Ф(Z). Из табл. 2.9 имеем =1,25. Верхняя граница потребности в деталях составит =5.04. Следовательно, с вероятностью 90% можно полагать, что за 150 тыс. км пробега потребуется не более 5 комплектов накладок сцепления. Средний же расход составит около 3,8 комплектов.

Таким образом, используя значе­ния параметра потока отказов, мож­но определить конкретный расход деталей за любой заданный период и планировать работу системы снаб­жения.

Параметр потока отказов может быть оценен на основании экспери­ментальных данных (отчетных мате­риалов, специальных наблюдений) следующим образом (см. рис. 2.15):

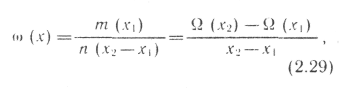
где m(x) – суммарное число отказов n автомобилей в интервале от х₁ до х₂ (или времени работы от t₁ до t₂); и - ведущие функции потока отказов к пробегу х₁ и х₂.

В общем случае параметр потока отказов непостоянен во времени, т. е. const. Наблюдаются три основных случая поведения парамет­ра по наработке.

Первый случай (рис. 2.17, а, 1) -полное восстановление ресурса после каждого отказа, т. е. = const; = 1.

При этом происходит стабилиза­ция параметра потока отказов на уровне .

Второй случай (рис. 2.17, а, 2) -неполное, но постоянное восстанов­ление ресурса после первого отказа, т. е. 1> =const. Для этого случая также характерна стабилизация па­раметра потока отказов, но на более высоком уровне:

Третий случай (рис. 2.17, а, 3) – последовательное снижение полноты восстанов­ления ресурса, т. е.

const; 1> > >… .

В этом случае и параметр потока отказов непрерывно увеличивается, что приводит к постоянному повыше­нию нагрузки на ремонтные подраз­деления предприятия. Однако при расчетах для этого случая можно принимать = const как среднюю для отдельных периодов 4, 5 и 6, на которые разбивается весь пробег или время работы автомобиля. Подоб­ный подход возможен также при анализе изменения параметра пото­ка отказов в течение года (рис. 2.17,6). Этот параметр может приниматься практически постоян­ным для зимнего ( ₃), осенне-весеннего ( ₀, _в) и летнего периодов.