19. Логарифмическое дифференцирование. Производные функций

Логарифмической производной функции y=f(x) называется производная ее логарифма.   тогда производная функции y=f(x) может быть найдена так:  . Рассмотрим степенную функцию     Имеем    тем самым формула доказана. Применив прием логарифмического дифференцирования, мы можем вычислить производную показательно-степенной функции  . Имеем, функции u(x) v(x) дифференцируемыми в т. x, а функцию u(x)>0 в некоторой окрестности т.x:   

20. Производная обратной функции. Производные .

_{Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией.} Пусть   - дифференцируемая функция от аргумента x в некотором интервале  . Если в уравнении   y считать аргументом, а x - функцией, то возникает новая функция  , где   - функция обратная данной. Для дифференцируемой функции с производной, отличной от нуля, производная обратной функции равна обратной величине производной данной функции, т.е

• ,

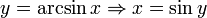21 Производные высших порядков

Пусть мы нашли для функции y=f(x) ее производную y = f (x). Производная от этой производной называется производной второго порядка функции f(x), или второй

производной, и обозначается  .

Аналогично определяются и обозначаются:

производная третьего порядка -  ,

производная четвертого порядка - 

и вообще производная n-го порядка -  .

Пример 3.15. Вычислить производную функции y=(3x³-2x+1)sin x.

Решение. По правилу 3, y'=(3x³-2x+1)'sin x + (3x³-2x+1)(sin x)' =

= (9x²-2)sin x + (3x³-2x+1)cos x.

22. Определение дифференциала. Геометрический смысл дифференциала.

Дифференциа́л (— разность, различие) — линейная часть приращения функции. Обычно дифференциал функции f обозначается df. Некоторые авторы предпочитают обозначать df шрифтом прямого начертания, желая подчеркнуть, что дифференциал является оператором.

Дифференциал в точке x₀ обозначается  , а иногда   или df[x₀], а также df, если значение x₀ ясно из контекста.

Соответственно, значение дифференциала в точке x₀ от h может обозначаться как  , а иногда   или df[x₀](h), а также df(h), если значение x₀ ясно из контекста.

Рассмотрим функцию y=f(x) и соответствующую ей кривую. Возьмем на кривой произвольную точку M(x; y), проведем касательную к кривой в этой точке и обозначим через α угол, который касательная образует с положительным направлением оси Ox. Дадим независимой переменной xприращение Δx, тогда функция получит приращение Δy =NM₁. Значениям x+Δx и y+Δy на кривой y = f(x) будет соответствовать точка

M₁(x+Δx; y+Δy).

Из ΔMNT находим NT=MN·tg α. Т.к. tg α = f '(x), а MN = Δx, тоNT = f '(x)·Δx. Но по определению дифференциала dy=f '(x)·Δx, поэтому dy = NT.

Таким образом, дифференциал функции f(x), соответствующей данным значениям x и Δx, равен приращению ординаты касательной к кривой y=f(x) в данной точке х.