15.Производные суммы, произведения функций

Производная суммы (разности) функций

Производная алгебраической суммы функций выражается следующей теоремой.

Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций:

Производная конечной алгебраической суммы дифференцируемых функций равна такой же алгебраической сумме производных слагаемых. Например,

Производная произведения функций.

Пусть u(x) и u(x) - дифференцируемые функции. Тогда произведение функций u(x)v(x) также дифференцируемо и

Производная произведения двух функций не равана произведению производных этих функций.

16.Производная частного двух функций. Производные tg x, ctg x.

Производная частного функций. Пусть u(x) и u(x) - дифференцируемые функции. Тогда, если v(x) ≠ 0, то производная частного этих функций вычисляется по формуле

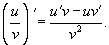
Пример 1

Найти производную функции  . Решение. Используем правило для вычисления производной частного.

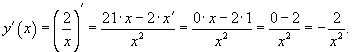
17. Производная сложной функции Производная сложной функции:

Если функция u(x) дифференцируема в точке x₀, а функция y = f(u) дифференцируема в точке u₀ = f(x₀), то сложная функция F(x) = f(u(x)) дифференцируема в точке x₀, причем:

F '(x0) = f '(u(x0))u' (x0).

Сложная функция, функция от функции. Если величина y является функцией от u, то есть у = f (u), а и, в свою очередь, функцией отх, то есть u = j(х), то у является Сложная функция от х, то есть y = f [(x)], определённой для тех значений х, для которых значения j(х) входят в множество определения функции f (u). В таком случае говорят, что у является Сложная функция независимого аргумента х, а u - промежуточным аргументом. Например, если у = u², u = sinx, то у = sin²х для всех значений х. Если же, например, у = , u = sinx, то у =  , причём, если ограничиваться действительными значениями функции, Сложная функция у как функциях определена только для таких значений х, для которых sin ³ 0, то есть для  , где k = 0, ± 1, ± 2,...   Производная Сложная функция равна произведению производной данной функции по промежуточному аргументу на производную промежуточного аргумента по независимому аргументу. Это правило (цепное правило) распространяется на Сложная функция с двумя, тремя и т. д. промежуточными аргументами: если у = f (u₁), u₁ = j(u₂),..., u_k-1 = j_k-1(u_k), u_k = j_k (x), то 

18. Производная неявной и параметрически заданной функции

Производная параметрически заданной функции

Если функция f задана параметрически

x = φ(t), y = ψ(t), α < t < β,

где y = f(x) и функции φ и ψ дифференцируемы, причем φ'(t) ≠ 0, то

Производная неявно заданной функции

Если y = f(x) - дифференцируемая функция, заданная уравнением F(x, y) = 0, т. е. F(x, f(x)) ≡ 0 на некотором интервале ]a, b[, то во многих случаях ее производную можно найти из уравнения