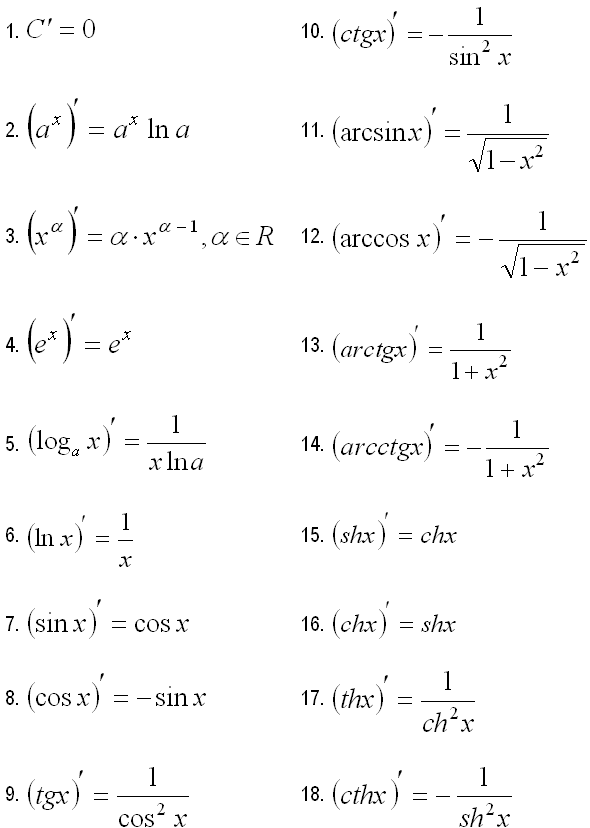- •Комплексное число. Алгеброическая, тригонометрическая и показательные формы записи.
- •Действия над комплексными числами. Возведение в степень. Извлечение корня n-ой степени.
- •Понятие функции. Способы задания
- •Аналитический способ
- •Графический способ. Числовые функции можно также задавать с помощью графика. Пусть - вещественная функция n переменных.
- •4.Числовая последовательность, ее предел. Свойства пределов.
- •Свойства пределов функции
- •Предел функции
- •6.Бесконечно малые и бесконечно большие функции
- •7. Сравнение бесконечно малых и бесконечно больших функций.
- •8. Первый замечательный предел. Следствия.
- •9.Второй замечательный предел. Следствия.
- •10.Непрерывность функции. Односторонние пределы.
- •11. Классификация точек разрыва.
- •12. Производная. Физический и геометрический смысл
- •Физический смысл производной.
- •13. Связь между непрерывностью и дифференцируемостью функции
- •Правила дифференцирования
- •15.Производные суммы, произведения функций
- •17. Производная сложной функции Производная сложной функции:
- •18. Производная неявной и параметрически заданной функции
- •19. Логарифмическое дифференцирование. Производные функций
- •20. Производная обратной функции. Производные .
- •21 Производные высших порядков
- •23. Теорема Роля
- •25. Теорема Коши.
- •28. Формула Тейлора для многочлена
- •29. Формула Тейлора для функций
- •32. Выпуклость, вогнутость, точки перегиба
- •33. Асимптоты кривой
- •35. Задачи на наибольшее и наименьшее значение функций
- •36. Понятие первообразной. Неопределённый интеграл. Его свойства
- •41. Интегрирование иррациональных выражений
- •42. Определённый интеграл. Определение. Геометрический смысл
- •43. Определённый интеграл. Свойства
- •44. Интеграл с переменным верхним пределом
- •45. Формула Ньютона – Лейбница
12. Производная. Физический и геометрический смысл
Произво́дная — функция, являющаяся результатом применения той или иной операции дифференцирования к исходной функции. Физический смысл производной — скорость изменения величины или процесса. Разновидности:
Производная функции
Производная (обобщения)
Частная производная
Производная по направлению
Произво́дное множество множества A — совокупность всех предельных точек этого множества.
Физический смысл производной.
Для неравномерного прямолинейного движения производная от пути по времени в момент t равна мгновенной скорости в этот момент.
-
Геометрический смысл производной.
Производная функции в точке х равна угловому коэффициенту касательной, проведенной к графику функции в этой точке:
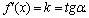
Пусть теперь точка М графика функции у = f(x)обладает абсциссойх0 и ординатой у0 = f(х0). Уравнение касательной МС (как прямой) в виде с угловым коэффициентом k = tgα = у´(х0) есть у = kх + b.
Подставим в это уравнение координаты точки М:
у0 = kх0 + b.
Исключим параметр b , вычтя из первого уравнения второе. Получим уравнение касательной, проведенной
к графику функции у = f(х) в точке с координатами х0,у0 :
у – у0 = k(х – х0) , где k = f ´(х0)
13. Связь между непрерывностью и дифференцируемостью функции
Из уже известных
нам свойств пределов очевидно, что
если функция у(x) имеет конечный
предел |
То, что обратное неверно, видно из примера: Рассмотрим функцию |
|
Предел слева существует, конечен и равен пределу справа, и значение функции в точке совпадает со значением предела. Следовательно функция непрерывна в нуле. 2. Выражение для производной функции у |
Имеет в точке x=0 левый предел (-1), а правый предел – (+1), а это означает, что предела она не имеет, то есть производной в точке х=0 не существует. Видим, что функция, непрерывна в точке х=0, производной в этой точке не имеет. |
14. Правила дифференцирования.
Производные некоторых элементарных
функций (![]() ,
xn
,
,
xn
,![]()
![]()
![]() ,
ln x)
,
ln x)
Правила дифференцирования
При
дифференцировании константу можно
выносить за производную:
![]() Правило
дифференцирования суммы функций:
Правило
дифференцирования суммы функций:
![]() Правило
дифференцирования разности
функций:
Правило
дифференцирования разности
функций:
![]() Правило
дифференцирования произведения функций
(правило Лейбница):
Правило
дифференцирования произведения функций
(правило Лейбница):
![]() Правило
дифференцирования частного
функций:
Правило
дифференцирования частного
функций:
![]() Правило
дифференцирования функции в степени
другой функции:
Правило
дифференцирования функции в степени
другой функции:
![]() Правило
дифференцирования сложной
функции:
Правило
дифференцирования сложной
функции:
![]() Правило
логарифма при дифференцировании
функции:
Правило
логарифма при дифференцировании
функции:
![]()