
- •Комплексное число. Алгеброическая, тригонометрическая и показательные формы записи.
- •Действия над комплексными числами. Возведение в степень. Извлечение корня n-ой степени.
- •Понятие функции. Способы задания
- •Аналитический способ
- •Графический способ. Числовые функции можно также задавать с помощью графика. Пусть - вещественная функция n переменных.
- •4.Числовая последовательность, ее предел. Свойства пределов.
- •Свойства пределов функции
- •Предел функции
- •6.Бесконечно малые и бесконечно большие функции
- •7. Сравнение бесконечно малых и бесконечно больших функций.
- •8. Первый замечательный предел. Следствия.
- •9.Второй замечательный предел. Следствия.
- •10.Непрерывность функции. Односторонние пределы.
- •11. Классификация точек разрыва.
- •12. Производная. Физический и геометрический смысл
- •Физический смысл производной.
- •13. Связь между непрерывностью и дифференцируемостью функции
- •Правила дифференцирования
- •15.Производные суммы, произведения функций
- •17. Производная сложной функции Производная сложной функции:
- •18. Производная неявной и параметрически заданной функции
- •19. Логарифмическое дифференцирование. Производные функций
- •20. Производная обратной функции. Производные .
- •21 Производные высших порядков
- •23. Теорема Роля
- •25. Теорема Коши.
- •28. Формула Тейлора для многочлена
- •29. Формула Тейлора для функций
- •32. Выпуклость, вогнутость, точки перегиба
- •33. Асимптоты кривой
- •35. Задачи на наибольшее и наименьшее значение функций
- •36. Понятие первообразной. Неопределённый интеграл. Его свойства
- •41. Интегрирование иррациональных выражений
- •42. Определённый интеграл. Определение. Геометрический смысл
- •43. Определённый интеграл. Свойства
- •44. Интеграл с переменным верхним пределом
- •45. Формула Ньютона – Лейбница
8. Первый замечательный предел. Следствия.
Первым
замечательным пределом называется
предел![]() Пользуемся
теоремой. ( Если
функция
Пользуемся
теоремой. ( Если
функция ![]() имеет
оба односторонних предела при
имеет
оба односторонних предела при ![]() и
эти пределы равны одному и тому же
числу
и
эти пределы равны одному и тому же
числу ![]() ,
то существует двусторонний предел
,
то существует двусторонний предел ![]() ,
который также равен
;
ноаборот, если существует двусторонний
предел
,
который также равен
;
ноаборот, если существует двусторонний
предел ![]() ,
то существуют оба односторонних предела
и оба они равны числу
).
,
то существуют оба односторонних предела
и оба они равны числу
).
Следствия:
Следствия
9.Второй замечательный предел. Следствия.
![]() или
или
![]()
Зная, что второй
замечательный предел верен для
натуральных значений x, докажем второй
замечательный предел для вещественных
x, то есть докажем, что ![]() .
Рассмотрим два случая:
.
Рассмотрим два случая:
1. Пусть ![]() .
Каждое значение x заключено между двумя
положительными целыми числами:
.
Каждое значение x заключено между двумя
положительными целыми числами: ![]() ,
где
,
где ![]() —
это целая часть x.
—
это целая часть x.
Отсюда следует: ![]() ,
поэтому
,
поэтому
![]() .
.
Если
,
то ![]() .
Поэтому, согласно пределу
.
Поэтому, согласно пределу ![]() ,
имеем:
,
имеем:
![]()
![]() .
.
По признаку (о пределе
промежуточной функции) существования
пределов ![]() .
.
2. Пусть ![]() .
Сделаем подстановку − x = t,
тогда
.
Сделаем подстановку − x = t,
тогда
![]()
![]() .
.
Из двух этих случаев
вытекает, что
для
вещественного x. ![]()
Следствия
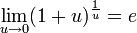
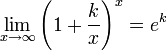
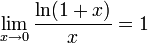
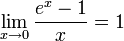
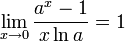 для
для  ,
, 

10.Непрерывность функции. Односторонние пределы.
Непрерывная функция — функция без «скачков», то есть такая у которой малые изменения аргумента приводят к малым изменениям значения отображения. График непрерывной функции можно начертить «не отрывая карандаш от бумаги».
Непрерывная функция вообще говоря, — синоним понятия непрерывное отображение, тем не менее, чаще всего этот термин используется в более узком смысле — для отображений между числовыми пространствами, например, на вещественной прямой. Эта статья посвящена именно непрерывным функциям, определённым на подмножестве вещественных чисел и принимающих вещественные значения.
Пусть
на некотором числовом множестве ![]() задана числовая
функция
задана числовая
функция ![]() и
число
и
число ![]() — предельная
точка области
определения
— предельная
точка области
определения ![]() .
Существуют различные определения для
односторонних пределов функции
.
Существуют различные определения для
односторонних пределов функции ![]() в
точке
,
но все они эквивалентны.
в
точке
,
но все они эквивалентны.
Односторо́нний преде́л в математическом анализе — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторо́нним преде́лом (или преде́лом сле́ва) и правосторо́нним преде́лом (или преде́лом спра́ва).
Основные свойства односторонних пределов идентичны свойствам обычных пределов и являются частными случаями свойств пределов вдоль фильтра.
Для существования (двустороннего) предела функции необходимо и достаточно, чтобы оба односторонних предела существовали и равнялись между собой.
11. Классификация точек разрыва.
Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке.
Классификация точек разрыва функции
Все точки разрыва функции разделяются на точки разрыва первого и второго рода. Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке
Существуют левосторонний предел
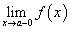 и
правосторонний предел
и
правосторонний предел 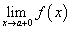 ;
;Эти односторонние пределы конечны.
При этом возможно следующие два случая:
Левосторонний предел и правосторонний предел равны друг другу:
![]()
Такая точка называется точкой устранимого разрыва.
Левосторонний предел и правосторонний предел не равны друг другу:
![]()
Такая
точка называется точкой
конечного разрыва.
Модуль разности значений односторонних
пределов![]() называется скачком
функции.
называется скачком
функции.
Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности.
