Предел функции

Предел функции — одно из основных понятий математического анализа. Функция f(x) имеет предел L в точке x₀, если для всех значений x, достаточно близких к x₀, значение f(x) близко к L.

Предел функции на бесконечности описывает поведение значения данной функции, когда её аргумент становится бесконечно большим (по абсолютной величине).

Обозначение предела функции

Предел функции обозначается как

или через символ предела функции:

6.Бесконечно малые и бесконечно большие функции

Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю. Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечности определённого знака.

Исчисление бесконечно малых — вычисления, производимые с бесконечно малыми величинами, при которых производный результат рассматривается как бесконечная суммабесконечно малых. Исчисление бесконечно малых величин является общим понятием для дифференциальных и интегральных исчислений, составляющих основу современной высшей математики. Понятие бесконечно малой величины тесно связано с понятием предела.

Бесконечно малая величина

Последовательность a_n называется бесконечно малой, если  . Например, последовательность чисел   — бесконечно малая.

Функция называется бесконечно малой в окрестности точки x₀, если  .

Функция называется бесконечно малой на бесконечности, если   либо  .

Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если  , то f(x) − a = α(x),  .

[править]Бесконечно большая величина

Во всех приведённых ниже формулах бесконечность справа от равенства подразумевается определённого знака (либо «плюс», либо «минус»). То есть, например, функцияxsin x, неограниченная с обеих сторон, не является бесконечно большой при  .

Последовательность a_n называется бесконечно большой, если  .

Функция называется бесконечно большой в окрестности точки x₀, если  .

Функция называется бесконечно большой на бесконечности, если   либо  .

Свойства бесконечно малых

• Сумма конечного числа бесконечно малых — бесконечно малая.

• Произведение бесконечно малых — бесконечно малая.

• Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.

• Если a_n — бесконечно малая последовательность, сохраняющая знак, то 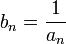  — бесконечно большая последовательность.

7. Сравнение бесконечно малых и бесконечно больших функций.

Сравнение бесконечно малых: Для определения бесконечно малых и бесконечно больших функций воспользуемся, так называемым сравнением функций. Пусть у нас есть две функции p(x) и q(x), которые стремятся к А при аргументе x стремящемся к А. И будем рассматривать предел их отношения при аргументе x, стремящемся к некоторому числу A. Тогда возможны следующие варианты:

1)   , т.е. предел отношения функций существует и он равен нулю, в этом случае говорят, что p(x) бесконечно малая функция более высокого порядка и принято обозначать p(x) = o(q(x)).

2)   , т.е. предел отношения функций существует и он равен С - некоторой константе, в этом случае говорят, что p(x) и q(x) бесконечно малые функции одного порядка и принято обозначать p(x) = O(q(x)).

3) Если данный предел:   не существует, в этом случае мы ничего не можем сказать о сравниваемых функциях и поэтому говорят, что функции не сравнимы.

4)  , т.е. предел отношения функций существует и он равен бесконечности, в этом случае говорят, что g(x) бесконечно малая функция более высокого порядка и принято обозначать q(x) = o(p(x)).

Устали от учебы? База затока приезжай в любое время года и наслаждайся незаюываемым по красоте морем.

Сравнение бесконечно больших: Также как и в предыдущем пункте будем рассматривать предел отношения двух функций. Только теперь у нас функции стремятся к бесконечности при аргументе x, стремящемся к А. Возможны следующие варианты:

1)  , т.е. предел отношения функций существует и равен бесконечности. В этом случае говорят, что p(x) бесконечно большая функция более высокого порядка.

2)  , т.е. предел отношения функций существует и равен С - некоторой константе. В этом случае говорят, что p(x) и q(x) бесконечно большие функции одного порядка.

3)  , т.е. предел отношения функций существует и равен нулю. В этом случае говорят, что q(x) бесконечно большая функция более высокого порядка.

4) Если данный предел:   не существует, в этом случае мы ничего не можем сказать о сравниваемых функциях и поэтому говорят, что функции не сравнимы.