5. Меры связи.

70. Корреляионный анализ выявляет:

Степень связи параметров

Форму зависимости

Достоверности различия

Все перечисленное

71. Кросстабуляции (таблицы сопряженности) служат для:

Описания связи 2-х и более номинативных переменных

Описания связи многомерных данных

Описания связи Юстаса с Центром

Описания парной линейной связи по Пирсону

72. Коэффициент корреляции r Пирсона предназначен для оценки связи между:

Двумя переменными, измеренными в метрической шкале

Двумя переменными, измеренными в номинативной шкале

Тремя переменными

Бесконечным числом переменных

73. Коэффициент корреляции r Спирмена предназначен для оценки связи между:

Двумя переменными, распределения которых НЕ являются нормальными

Двумя переменными, измеренными в метрической шкале

Тремя переменными

Двумя переменными с нормальными распределениями

74.

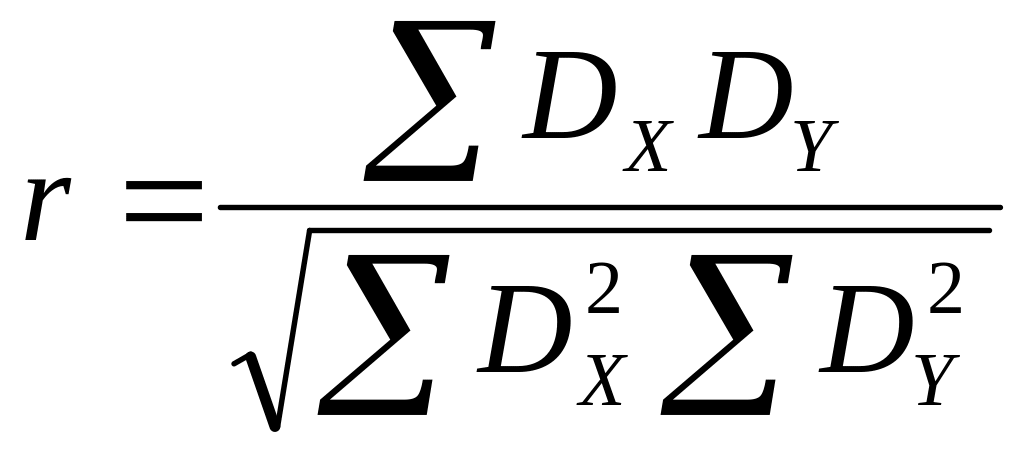
Это формула расчета

Коэффициент корреляции r Пирсона

Коэффициент корреляции r Спирмена

Коэффициент корреляции r Гросмана

Коэффициент корреляции r Фишера

75. =СУММ(D1:D15)/КОРЕНЬ((СУММ(E1:E15)^2)*(СУММ(F1:F15)^2))

Это формула расчета в MS Excel (A15 и B15 – средние, А16 и B16 – ошибки средних)

Коэффициент корреляции r Пирсона

Коэффициент корреляции r Спирмена

Коэффициент корреляции r Гросмана

Коэффициент корреляции r Фишера

6. Регрессионный анализ.

76. Регрессионный анализ выявляет:

Форму зависимости

Степень связи параметров

Достоверности различия

Все перечисленное

77. Результатом регрессионно-корреляционного анализ является:

Вычисление коэффициентов уравнения связи B₀ и B_n

Коэффициент корреляции R

Сумма квадратов отклонений SS

Стандартное отклонение SD

78. Линеаризация функций проводится с целью:

Приведения уравнения связи к линейному виду

Устранения случайной ошибки

Избегания сложных вычислений

Стандартное отклонение SD

79. a = y – bx

Это формулы для вычисления коэффициентов уравнения

Линейной зависимости y = a + bx

Степенной зависимости y = ax^b

Квадратичного корня y = (a + bx)²

Показательной зависимости y = ae^bx

80. Линеаризация функций вызвана:

Отсутствием формул для расчета коэффициента корреляции для нелинейных зависимостей

Упрощением вида функций

Облегчением счета в уме

Дополнительными проверками функционирования компьютера

7. Основные понятия теории статистического вывода

81. Нормальное распределение вероятностей иллюстрируется:

кривой Гаусса

прямой Штрауса

синусоидой Пуассона

гиперболой Гарина

82. Найти доверительный интервал для оценки с надежностью неизвестного математического ожидания а нормально распределенного признака Х генеральной совокупности, если известны выборочная средняя , генеральное среднеквадратическое отклонение и объём выборки n =10,2; =4; n=16; = 0,99 (вычисления выполнять с точностью до двух знаков после запятой)

(7,63; 12,77)

(8,24; 12;16)

(9,56; 10,84)

(7,55; 12,85)

83. По выборке из 25 случаев измерения простой сенсомоторной реакции среднее время составило 101 мс с исправленным средним квадратическим отклонением 3 мс. Построить доверительный интервал для среднего с вероятностью 90 %. Предполагается, что время – это нормально распределенная случайная величина.

(99,974;102,026)

(100,208; 101,792)

(97,04; 104,96)

(100,568; 101,342)

84. Респондент выполняет тест «Простая сенсомоторная реакция». Известно, что респондент выполняет тест со стандартным отклонением . Выборка 50 опытов показала среднее время 125,8 мс. Найти доверительный интервал для среднего времени в генеральной совокупности с вероятностью 95 %. Генеральная совокупность распределена нормально.

(123,03; 128,57)

(125,52; 126,08)

(124,39; 127,21)

(115,8; 135,8)

85. По выборке из 25 случаев измерения простой сенсомоторной реакции среднее время составило 101 мс с исправленным средним квадратическим отклонением 3 мс. Построить доверительный интервал для дисперсии с вероятностью 90 %. Предполагается, что время – это нормально распределенная случайная величина.

(5,93;15,65)

(6,51;13,76)

(2,17; 4,59)

(5,72; 14,79)

86. По данным выборки объема n=30 из генеральной совокупности нормально распределенного количественного признака найдено среднее квадратическое отклонение SD=14. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение SD с надежностью .

(11,15;18,85)

(11,34;19,17)

(11,59;17,83)

(9,6; 22,7)

87. Для психологического исследования составлена случайная выборка из 19 фирм. По выборке оказалось, что в фирме в среднем работают 77,5 человека при среднем квадратическом отклонении 25 человек. Пользуясь 95 % доверительным интервалом, оценить среднее число работающих в фирме по всей отрасли. Предполагается, что количество работников фирмы имеет нормальное распределение.

(66,46;85,54)

(67,58;87,42)

(75,22; 79,79)

(75,09; 79,91)