8. Статистические критерии.
88. При каких условиях применяются параметрические методы сравнения двух выборок:
Признаки измерены в интервальной шкале или шкале отношений.
Признаки измерены в номинальной или порядковой шкале
89. При каких условиях применяются НЕ параметрические методы сравнения двух выборок:
Признаки измерены в номинальной или порядковой шкале
Признаки измерены в интервальной шкале или шкале отношений.
90. При каких условиях применяются параметрические методы сравнения двух выборок:
Распределение соответствует нормальному закону
Распределение НЕ соответствует нормальному закону
91. При каких условиях применяются НЕ параметрические методы сравнения двух выборок:
Распределение НЕ соответствует нормальному закону
Распределение соответствует нормальному закону
92. При каких условиях применяются параметрические методы сравнения двух выборок:
Выборка имеет большой объем
Выборка мала, чтобы судить о распределении в генеральной совокупности.
93. При каких условиях применяются НЕ параметрические методы сравнения двух выборок:
Выборка мала, чтобы судить о распределении в генеральной совокупности.
Выборка имеет большой объем
94. Метод вычисления достоверности различия средних по критерию t-Стьюдента проводится только в следующем случае:
Все перечисленные.
Для одной выборки
Для независимых выборок
Для связанных выборок
95. Метод вычисления достоверности различия выборок по критерию U-Манна-Уитни для проводится только в следующем случае:
Для независимых выборок
Все перечисленные.
Для одной выборки
Для связанных выборок
96. Метод вычисления достоверности различия по критерию W-Вилкоксона проводится только в следующем случае:
Для сопряженных пар
Для одной выборки
Для независимых выборок
Для связанных выборок
97. Пороговое значение t-Стьюдента определяется по таблице на основе:
Количества степеней свободы df и значения достоверности p
Объема выборки n и стандартного отклонения SD
Суммы квадратов SS и ошибки среднего m
Среднего арифметического M и дисперсии δ2
98.
- Это формулы расчета
Критерия Стьюдента для одной выборки
Критерия Стьюдента для независимых выборок
Критерия Стьюдента для независимых выборок разного объема
Критерия Стьюдента для зависимых выборок
99. =(B100-B50)/(КОРЕНЬ(СУММ(А1:A100)/100)/КОРЕНЬ(100)) -Это формула расчета в MS Excel (B100 – среднее всей выборки, B50 – среднее части выборки)
Критерия Стьюдента для одной выборки
Критерия Стьюдента для независимых выборок
Критерия Стьюдента для независимых выборок разного объема
Критерия Стьюдента для зависимых выборок
100.
- Это формулы расчета
Критерия Стьюдента для независимых выборок
Критерия Стьюдента для одной выборки
Критерия Стьюдента для независимых выборок разного объема
Критерия Стьюдента для зависимых выборок
101. =(A15-B15)/КОРЕНЬ(A16^2+B16^2)
Это формула расчета в MS Excel (A15 и B15 – средние, А16 и B16 – ошибки средних)
Критерия Стьюдента для независимых выборок
Критерия Стьюдента для одной выборки
Критерия Стьюдента для независимых выборок разного объема
Критерия Стьюдента для зависимых выборок
102.
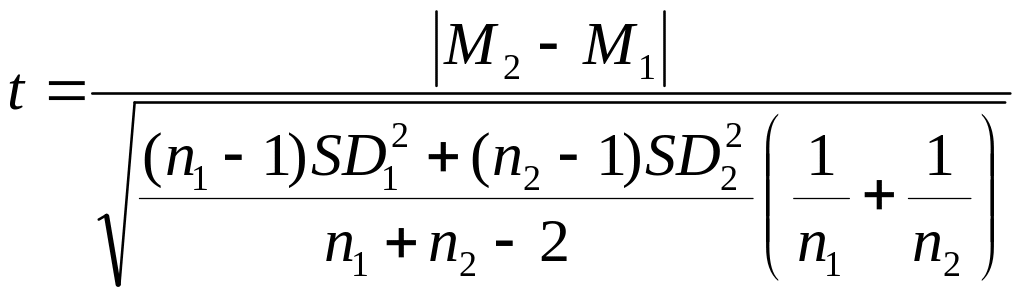- Это формулы расчета
Критерия Стьюдента для независимых выборок разного объема
Критерия Стьюдента для независимых выборок
Критерия Стьюдента для одной выборки
Критерия Стьюдента для зависимых выборок
103. =(A16-B21)/КОРЕНЬ((1/15+1/20)*((15-1)*A17^2+(20-1)*B22^2)/(15+20-2)) - Это формула расчета в MS Excel (A16 и B21 – средние, А17 и B22 – стандартные отклонения)
Критерия Стьюдента для независимых выборок разного объема
Критерия Стьюдента для независимых выборок
Критерия Стьюдента для одной выборки
Критерия Стьюдента для зависимых выборок
104.
Это формулы расчета
Критерия Стьюдента для зависимых выборок
Критерия Стьюдента для одной выборки
Критерия Стьюдента для независимых выборок
Критерия Стьюдента для независимых выборок разного объема
105. =A20/B20
Это формула расчета в MS Excel (A20 – среднее разницы, B20 – ошибка среднего разницы)
Критерия Стьюдента для зависимых выборок
Критерия Стьюдента для одной выборки
Критерия Стьюдента для независимых выборок
Критерия Стьюдента для независимых выборок разного объема
106. Процентной
точке
хи-квадрат распределения с числом
степеней свободы
соответствует
вероятность
:
0,975
0,025
0,95
0,05
107. Процентной
точке
–
распределения с числом степеней свободы
числителя
и знаменателя
соответствует
вероятность
:
0,95
0,025
0,975
0,05
108. Процентной
точке
распределения Стьюдента с числом
степеней свободы
соответствует
вероятность
:
0,975
0,025
0,95
0,05