2. Графическое представление данных
6. На графике изображен(-а):
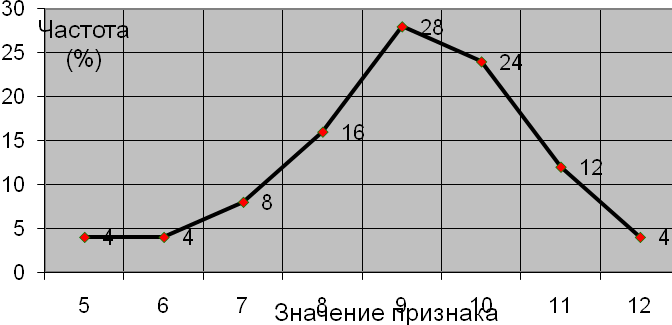
Полигон распределения частот
Гистограмма распределения
Кумулята распределения
Временной ряд
7. На графике изображен(-а):
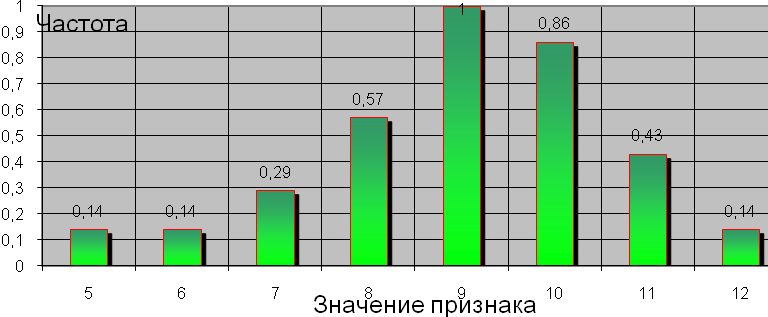
Гистограмма распределения
Полигон распределения частот
Кумулята распределения
Временной ряд
8. На графике изображен(-а):
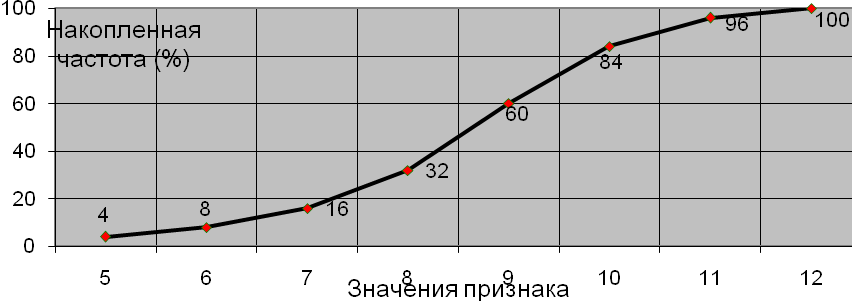
Кумулята распределения
Гистограмма распределения
Полигон распределения частот
Временной ряд
3. Меры центральной тенденции
9. Характеристики диапазона распределения:
Минимум. Максимум. Размах. Сумма
Среднее значение. Медиана. Мода
Дисперсия. Стандартное отклонение.
Стандартная ошибка
10. Меры центральной тенденции:
Среднее значение. Медиана. Мода
Дисперсия. Стандартное отклонение.
Минимум. Максимум. Размах. Сумма
Экцесс. Асимметрия.
11. Ошибка среднего:
Стандартная ошибка
Экцесс. Асимметрия.
Среднее значение. Медиана. Мода
Минимум. Максимум. Размах. Сумма
12.
- Это формула расчета
Среднего значения.
Стандартной ошибки
Экцесса.
Асимметрии.
13. =СРЗНАЧ (А1:А13) Это формула расчета в MS Excel
Среднего значения.
Стандартной ошибки
Экцесса.
Асимметрии.
14. D=(xi – M)
Это формула расчета
Отклонения
Стандартной ошибки
Экцесса.
Асимметрии.
15. =А1-А$14
Это формула расчета в MS Excel (в ячейке А14 – значение среднего арифметического)
Отклонения
Стандартной ошибки
Экцесса.
Асимметрии.
16. =(А1-А$14)^2
Это формула расчета в MS Excel (в ячейке А14 – значение среднего арифметического)
Квадрата отклонений
Стандартной ошибки
Экцесса.
Асимметрии.
17.
- Это формула расчета
Суммы квадратов отклонений.
Стандартной ошибки
Экцесса.
Асимметрии.
18. =СУММ(А1:А13) - Это формула расчета в MS Excel
Суммы
Стандартной ошибки
Экцесса.
Асимметрии.
19.
- Это формула
расчета
Стандартного отклонения для выборки n≥30
Стандартного отклонения для выборки n<30
Стандартной ошибки
Асимметрии
20. =КОРЕНЬ(СУММ(А1:А13)/13) - Это формула расчета в MS Excel
Стандартного отклонения для выборки n≥30
Стандартной ошибки
Экцесса.
Асимметрии.
21.
- Это формула расчета
Стандартного отклонения для выборки n<30
Стандартного отклонения для выборки n>30
Стандартной ошибки
Асимметрии
22. =КОРЕНЬ(СУММ(А1:А13)/12) - Это формула расчета в MS Excel
Стандартного отклонения для выборки n<30
Стандартного отклонения для выборки n>30
Стандартной ошибки
Асимметрии
23.
- Это формула расчета
Ошибки среднего
Стандартного отклонения
Стандартной ошибки
Асимметрии
24. =КОРЕНЬ(СУММ(А1:А13)/12)/КОРЕНЬ(13) - Это формула расчета в MS Excel
Ошибки среднего для выборки n<30
Стандартного отклонения
Стандартной ошибки
Асимметрии
25. =КОРЕНЬ(СУММ(A1:A13)/13)/КОРЕНЬ(13) - Это формула расчета в MS Excel
Ошибки среднего для выборки n≥30
Стандартного отклонения
Стандартной ошибки
Асимметрии
26. Дано статистическое распределение выборки:
хi |
-2 |
1 |
2 |
3 |
4 |
5 |
ni |
2 |
1 |
2 |
2 |
2 |
1 |
Найти медиану вариационного ряда
2,5
2
3
5
27. Дано статистическое распределение выборки:
хi |
-2 |
1 |
2 |
3 |
4 |
5 |
ni |
3 |
2 |
2 |
3 |
3 |
7 |
Найти точечную оценку генеральной средней
2,8
2,4
3
2,5
28. Дано статистическое распределение выборки:
хi |
-2 |
1 |
2 |
3 |
4 |
5 |
ni |
4 |
3 |
3 |
4 |
4 |
2 |
Найти моду вариационного ряда
не определена
3,5
4
2,5
29. В таблице представлены данные о распределении 100 респондентов по баллам теста:
хi |
30-40 |
40-50 |
50-60 |
60-70 |
70-80 |
80-90 |
90-100 |
ni |
2 |
4 |
12 |
18 |
21 |
24 |
19 |
Найти выборочное среднее.
75
76
85
60
30. В таблице представлены данные о распределении 100 респондентов по баллам теста:
хi |
30-40 |
40-50 |
50-60 |
60-70 |
70-80 |
80-90 |
90-100 |
ni |
7 |
9 |
17 |
23 |
22 |
22 |
0 |
Найти выборочную моду.
68,57
66
65
не определена
31. В таблице представлены данные о распределении 100 респондентов по баллам теста:
хi |
30-40 |
40-50 |
50-60 |
60-70 |
70-80 |
80-90 |
90-100 |
ni |
8 |
10 |
18 |
24 |
22 |
10 |
8 |
Найти выборочную медиану.
65,83
68,57
70
65
32. Из приведенного ниже списка к выборочным характеристикам положения распределения относится:
выборочная мода
выборочный коэффициент асимметрии
выборочный коэффициент эксцесса
выборочный центральный момент второго порядка
33. Из приведенного ниже списка к выборочным характеристикам положения распределения относится:
выборочная средняя
размах выборки
выборочное среднее квадратическое отклонение
исправленная дисперсия
34. Из приведенного ниже списка к выборочным характеристикам положения распределения относится:
выборочная медиана
выборочный центральный момент первого порядка
размах выборки
выборочный коэффициент эксцесса
35.
- Это формула расчета
Вариативности
Критерия Стьюдента для независимых выборок
Стандартного отклонения
Суммы квадратов отклонений
36. Стандартное отклонение называют еще:
Квадратическим отклонением
Критерием Стьюдента
Средним арифметическим
Суммой квадратов отклонений
37. Среднее арифметическое называют еще:
Математическим ожиданием
Квадратическим отклонением
Критерием Стьюдента
Суммой квадратов отклонений
38. В электронной таблице MS Excel функция СРЗНАЧ позволяет вычислить
Математическое ожидание
Квадратическое отклонение
Критерий Стьюдента
Сумму квадратов отклонений
39. В электронной таблице MS Excel функция СТАНДАРТОТКЛОНП позволяет вычислить
Квадратическое отклонение
Математическое ожидание
Критерий Стьюдента
Сумму квадратов отклонений
40. Заданы две выборки значений случайной величины из генеральных совокупностей:
X: 13, 7, 24, 18, 7, 15
Y: 15, 6, 27, 19, 8, 23, 5, 13.
Для них одинаковой числовой характеристикой из приведенного списка является:
выборочная медиана.
среднеквадратическое отклонение
1-я квартиль
выборочная средняя
41. Заданы две выборки значений случайной величины из генеральных совокупностей:
X: 13, 5, 10, 8, 5, 21
Y: 15, 5, 24, 6, 5, 24, 5, 5.
Для них одинаковой числовой характеристикой из приведенного списка является:
выборочная мода
среднеквадратическое отклонение
2-я квартиль
выборочная медиана.
42. Заданы две выборки значений случайной величины из генеральных совокупностей:
X: 13, 15, 14, 8, 25, 21
Y: 12, 13, 15, 11, 16, 16, 16, 12.
Для них одинаковой числовой характеристикой из приведенного списка является:
2-я квартиль
выборочная дисперсия
выборочная мода
выборочная средняя.
43. Заданы две выборки значений случайной величины из генеральных совокупностей:
X: 11, 12, 17, 9, 10, 7
Y: 11, 12, 11, 10, 13, 9, 14, 8.
Для них одинаковой числовой характеристикой из приведенного списка является:
выборочная средняя
выборочная дисперсия
1-я квартиль
выборочная медиана
44. Заданы две выборки значений случайной величины из генеральных совокупностей:
X: 8, 3, 7, 4, 4, 4
Y: 7, 2, 4, 7, 6, 5, 4, 3.
Для них одинаковой числовой характеристикой из приведенного списка является:
1-я квартиль
выборочная медиана
выборочная мода
выборочная средняя.
45. Найти квантиль
выборки: 1,5, 8,7, 13,9, 4,6, 7,3, 5,9, 11,7, 3,1,
9,8, 12,4.
9,8
8,7
11,7
5,9
46. Найти квантиль
выборки: 66, 61, 67, 73, 51, 59, 48, 47, 58, 44.
51
48
73
67
47. Найти квантиль
выборки: 18, 17,7, 19, 22, 18 , 21, 21, 19, 20, 30.
20
19
22
18