15.3. Динамічні показники слідкуючого електропривода

Динамічні показники систем керування, зазвичай, визначають на підставі передавальних функцій. Для цього необхідно скласти рів-няння руху системи за рівняннями її елементів.

Для слідкуючого електропривода, принципова схема якого зоб-ражена на рис. 15.2, запишемо рівняння елементів, вважаючи, що їх статичні характеристики лінійні.

Рівняння сельсинів:

рівняння розузгодження сельсинів давача і приймача

; (15.6)

рівняння сельсина-приймача

, (15.7)

де – крутизна характеристики при .

Рівняння фазочутливого підсилювача

, (15.8)

де – коефіцієнт підсилення підсилювача.

Рівняння двофазного асинхронного двигуна

, (15.9)

де – еквівалентна електромагнітна стала часу кіл статора і рото-ра, яку можна наближено визначити за формулою ;

– електромеханічна стала часу; – коефіцієнт жорсткості лінеарезованої частини механічної характеристики; – коефіцієнт передачі двигуна.

Рівняння редуктора

. (15.10)

На підставі рівнянь (15.6) – (15.10) складають структурну схему слідкуючого електропривода (рис.15.4).

Рис. 15.4. Структурна схема слідкуючого електропривода

На структурній схемі додатково показані диференціальна ланка з

передавальною функцією , зворотний зв’язок за швид-кістю з коефіцієнтом зворотного зв’язку і момент статичного опору .

Розв’язавши систему з рівнянь (15.6) – (15.10), отримаємо рівняння розімкненої системи

, (15.11)

де , – коефіцієнт підсилення розімкненої системи.

Рівнянню (15.11) відповідає передавальна функція розімкненої системи

. (15.12)

Якщо ротор С-Д обертати зі сталою швидкістю , то і ротор С-П буде обертатись з такою же швидкістю. Підставивши в (15.11) , що відповідає , і , одержимо рівняння руху слідкуючого електропривода в усталеному режимі:

. (15.13)

Величина називається добротністю. Вона дозво-ляє визначити усталену похибку в режимі усталеного руху з . Отже, при заданій усталена похибка буде тим більша, чим менша добротність.

Перехідний процес в замкненій системі описує рівняння замкне-ної системи, яке отримаємо, підставивши в (15.11) :

. (15.14)

Рівняння (15.14) дозволяє визначити, за якого співвідношення , і система буде стійкою. За критерієм Рауса система буде стійкою, якщо коефіцієнти характеристичного рівняння будуть додатними числами і

. (15.15)

З (15.15) отримаємо умову стійкості:

, (15.16)

з якої слідує, що добротність повинна бути меншою за критичну , за якої система знаходиться на межі стійкості. Зазвичай, величина добротності повинна бути меншою за критич-ну, щоби забезпечити запаси стійкості за амплітудою 3-4 і за фазою .

При проектуванні слідкуючого електропривода за вимогами тех-нологічного процесу визначають допустиму усталену похибку при . Тоді розрахункова добротність

. (15.17)

Розглянемо такий приклад. Нехай , . Тоді . Приймемо .

Усталена похибка при . Якщо отримана похибка більша , то необхідно збільшити добротність за рахунок або збільшення коефіцієнта підсилення підсилювача, або передбачити додаткові впливи від елементів, показаних на рис.15.4 пунктирними лініями.

Розглянемо, як впливає на добротність від’ємний зворотний зв'я-зок за швидкістю двигуна з коефіцієнтом . Цей зворотний зв'язок змінить лише рівняння (15.8), яке тепер матиме вид

. (15.18)

З врахуванням (15.18) рівняння руху розімкненої системи буде таким:

, (15.19)

де – інтенсивність керування за швидкості двигуна.

Підставивши в (15.19) і , отримаємо рівняння руху в усталеному режимі

. (15. 20)

Добротність системи зі зворотним зв’язком за швидкістю

. (15.21)

З (15.21) випливає, що від’ємний зворотний зв'язок за швидкістю вихідного вала зменшує добротність системи у порівнянні з систе-мою без зворотного зв’язку, для якої вона дорівнює .

Для визначення впливу зворотного зв’язку на стійкість знайдемо рівняння рух замкненої системи, підставивши в (15.19) . В результаті отримаємо рівняння

, (15.22)

характеристичне рівняння якого

. (15.23)

Оскільки в (15.23) всі коефіцієнти додатні, то умова стійкості за критерієм Рауса матиме вид:

або

. (15.24)

Нерівність (15.24) показує, що введення в систему додатково зво-ротного зв’язку за швидкістю двигуна покращує стійкість, оскільки менше добротності . Величину коефіцієнта вибирають з умови запасу стійкості за фазою і за амплітудою, рівною 3-4. Крім того, цей зв'язок зменшує вплив мож-ливих змін сталих часу , і коефіцієнта на стійкість, але одночасно зростає усталена похибка .

Окрім від’ємних зворотних зв’язків в слідкуючому електропри-воді використовують і додатні зв’язки, зокрема за похідною від по-хибки. За такого додаткового зв’язку з коефіцієнтом пропорційнос-ті напруга на виході підсилювача.

. (15.25)

З врахуванням (15.25) рівняння руху розімкненої системи матиме вид:

, (15.26)

де – інтенсивність керування за похідною похибки.

В усталеному режимі з рівняння (15.26) матиме вид

. (15.27)

і добротність системи , тобто буде рівною добротності сис-теми без додаткових зв’язків .

Підставивши в (15.26) , отримаємо рівняння замкненої системи:

. (15.28)

Рівнянню (15.28) відповідає характеристичне рівняння

(15.29)

і згідно критерію Рауса умова стійкості матиме вид:

або

, (15.30)

оскільки всі коефіцієнти в (15.29) додатні.

З (15.30) слідує, що введення зв’язку за похідною від похибки покращує стійкість системи і не змінює усталеної похибки у порівнянні з системою без такого зв’язку.

Відомо, що для підвищення швидкодії використовують комбіно-вані системи керування – системи керування за відхиленням і за збуренням. Основним збуренням в слідкуючому електроприводі є задаючий сигнал. Тому розглянемо систему керування за відхилен-ням і похідною за задаючим сигналом (рис.15.4). Для такої системи напруга керування

, (15.31)

де – коефіцієнт пропорційності.

Розв’язавши систему рівнянь (15.6) – (15.11) з заміною (15.8) на (15.31), отримаємо рівняння замкненої комбінованої системи:

, (15.32)

де – інтенсивність керування за похідною від задаючо-го сигналу.

Для визначення усталеної похибки необхідно знати передавальну функцію системи за похибкою , де пере-давальна функція замкненої системи.

Передавальна функція замкненої системи згідно (15.32)

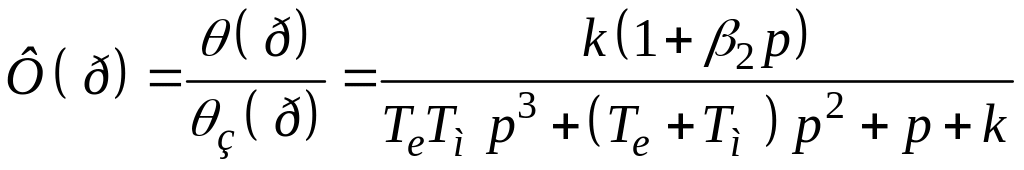. (15.33)

Звідси

. (15.34)

Передавальній функції відповідає характеристичне рів-няння , яке не відрізняється від характеристичного рівняння системи з керуванням за відхиленням (похибкою). Отже, введення додаткового сигналу за похідною кута повороту вхідного вала не змінює стійкість комбінованої системи у порівнянні з системою керування тільки за похибкою, але вона впливає на величину усталеної похибки.

Щоби визначити цей вплив, необхідно передавальну функцію розкласти у степеневий ряд. Тоді

, (15.35)

де , , ,…, – коефіцієнти похибок, які обчислюють за формулою

. (15.36)

Застосувавши до ряду (15.35) обернене перетворення Лапласа, одержимо новий ряд у виді:

. (15.37)

Кількість членів ряду (15.37), які використовують при розрахун-ках, залежить від виду задаючого сигналу. Так, для , досить визначити за формулою (15.36) коефіцієнти і , а для – коефіцієнти , і , бо старші похідні будуть дорівнювати нулю.

Згідно (15.36) коефіцієнти похибок , і функції (15.34) будуть такими:

;

;

. (15.38)

Отже, якщо , то усталена похибка

. (15.39)

З (15.39) слідує, що похідна за задаючим сигналом зменшує уста-лену похибку на у порівнянні з системою керування за похиб-кою. За умови усталена похибка і система стає інваріантною по відношенню до зміни задаючого сигналу.

Якщо , де – прискорення, то , і усталена похибка

. (15.40)

Рівняння (15.40) показує, що при рівноприскореному русі задаю-чого валу усталена похибка буде наростати з часом і тільки за умови вона буде сталою і рівною .

Отже, додаткові впливи від зворотного зв’язку за швидкістю, за похідною від похибки, чи задаючого сигналу дозволяють змінювати величину усталеної похибки. Одночасно змінюється передавальна функція замкненої системи і, як наслідок, – якісні показники пере-хідного процесу. Зміну останніх можна дослідити або за амплітуд-но-фазовими частотними характеристиками, визначаючи запас стій-кості за амплітудою і фазою, або за розв’язком рівняння руху замк-неної системи для різних законів зміни . Найбільш просто дослі-дити впливи додаткових зв’язків шляхом комп’ютерного моделюва-ння.

а б в

Рис. 15.5. Графіки і у випадках (а) і (б, в)

В режимі відпрацювання стрибка задаючого сигналу (позиційне керування) похибка змінюється від максимального значення до нуля і може мати коливально-затихаючий чи монотонний характер у за-лежності від виду коренів характеристичного рівняння системи (рис.15.5,а). Коли задаючий сигнал , то похибка спочатку зростає до максимального значення , а потім наближається до усталеного значення (рис.15.5,б) і тільки в системі з комбінованим керуванням усталена похибка з часом стає рівною нулю (рис.15.5,в).

Контрольні запитання і задачі

1. Що є структурною ознакою слідкуючого електропривода?

2. Що є характерним для дискретного слідкуючого електропри-вода?

3. Яке магнітне поле створює обмотка збудження сельсина-дава-ча?

4. Від чого залежить величина ЕРС, що наводиться в однофазній обмотці сельсина-приймача?

5. Якою буде усталена похибка в системі керування за похибкою, якщо добротність і ?

6. Як впливає від’ємний зворотний зв'язок за швидкістю двигуна на добротність слідкуючого електропривода?

7. Якою повинна бути добротність системи керування за похиб-кою і її похідною, якщо усталена похибка і ?

8. Як впливає додатковий вплив за похідною від похибки на стій-кість роботи слідкуючого електропривода?

9. В якій системі керування усталена похибка за умови ?

10. У чому відмінність слідкуючого електропривода від позицій-ного електропривода?

Розділ 16